A rectangular wire farme can be rotated through it arm PQ which is hinged along the y-axis as shown the figure . If the wire-frame has mass and externt magentic field is . The magnetic field at due to the current in the wire PQ will be have the direction (assume the wire-fram is the in horizontal equilibrium positive )
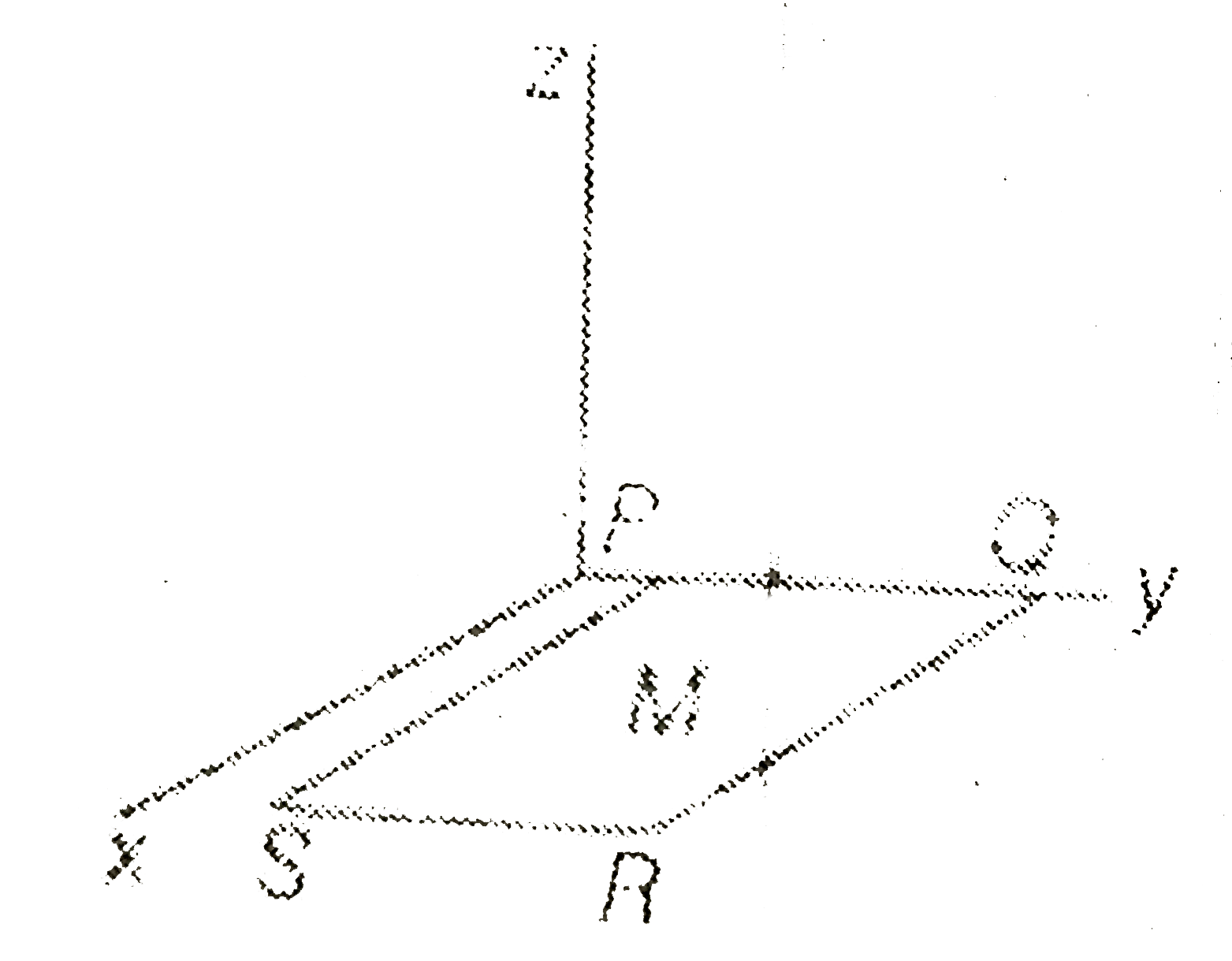
The correct Answer is:(i) 0 (ii) 6
(i) 0 (ii) 6
(i)Let the direction of current in wire PQ is from P to Q and its magnitude be I.
The magnetic moment of the given loop is
Torque on the loop due to magnetic force is
Torque of weight of the loop about axis PQ is
We see that when the current in the wire PQ is from P to Q and are in opposite directions, so they can cancel each other and the loop may remain in equilibrium. So, the direction of current I in wire PQ is from P to Q. Further for equilibrium of the loop
or

(ii) Magnetic force on wire RS is
Topper's Solved these Questions
- BOOK - VMC MODULES ENGLISHCHAPTER - MAGNETIC EFFECTS OF CURRENT EXERCISE - JEE Main (Archive)75videos
MAGNETIC EFFECTS OF CURRENT
- BOOK - VMC MODULES ENGLISHCHAPTER - LIQUIDSEXERCISE - JEE ADVANCED (LEVEL -2)55videos
LIQUIDS
- BOOK - VMC MODULES ENGLISHCHAPTER - MOCK TEST 1EXERCISE - PART I : PHYSICS (SECTION-2)10videos
MOCK TEST 1
Similar Questions
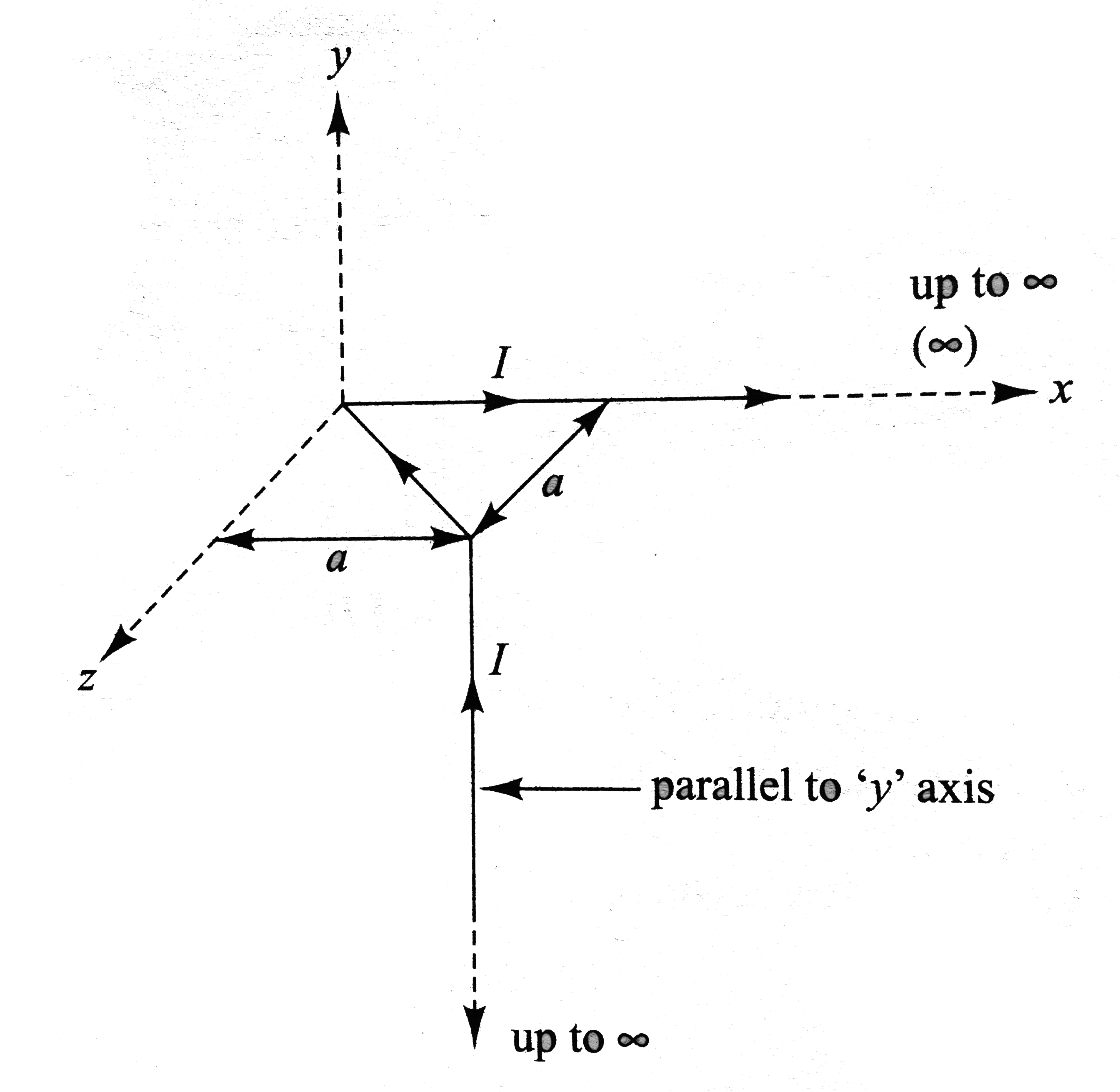
The magnetic field at the origin due to the current flowing in the wire is
 View Solution
View SolutionThe magnetic field at the origin due to the current flowing in the wire is
 View Solution
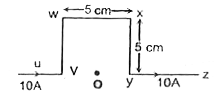
View SolutionThe magnetic field at O due to current in the infinite wire forming a loop as a shown in Fig.
 View Solution
View SolutionThe resulting magnetic field at the point O due to the current carrying wire shown in the figure:
 View Solution
View SolutionFind the magnitude and direction of magnetic field at point P due to the current carrying wire as shown in
 View Solution
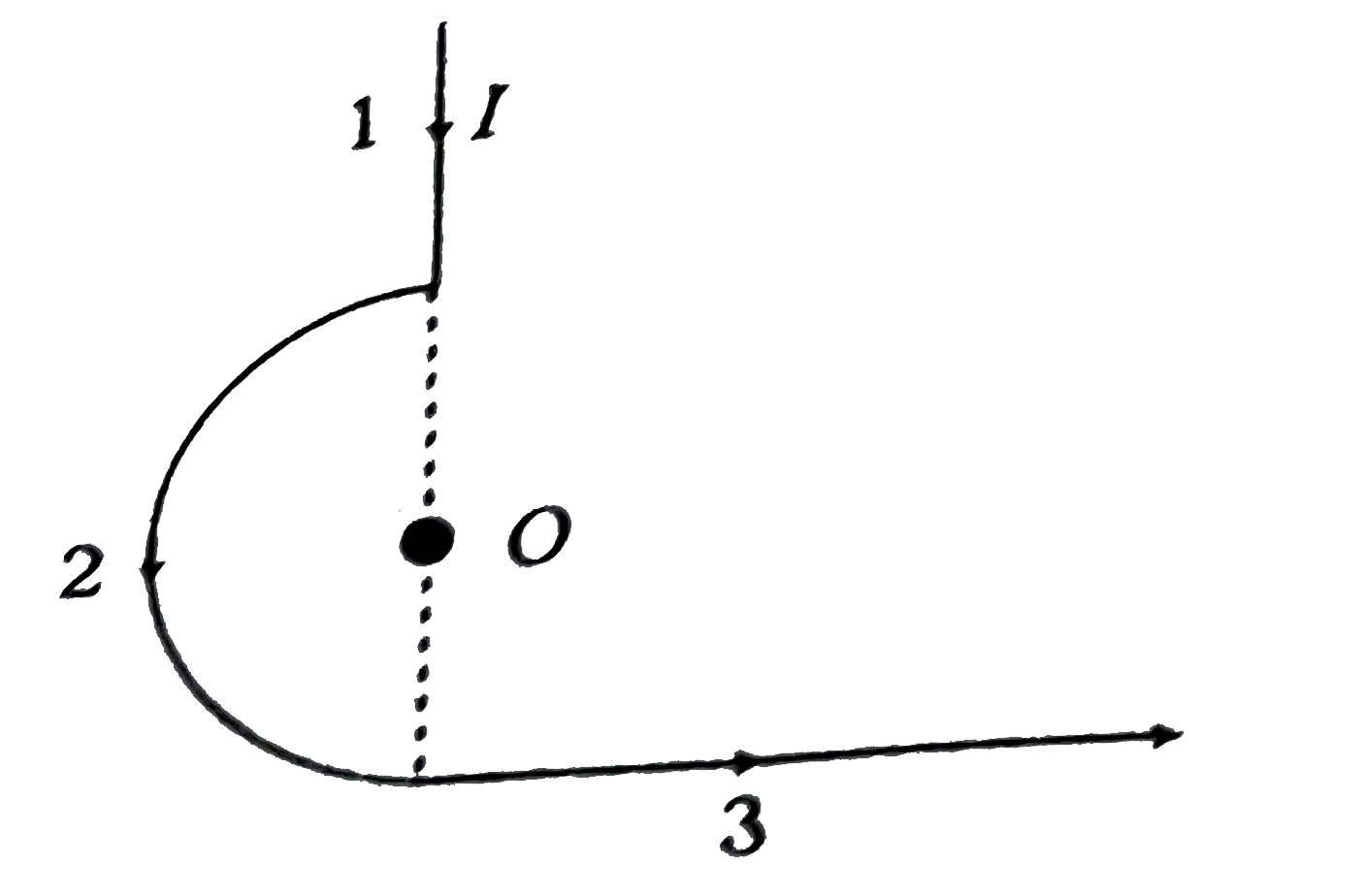
View SolutionMagnetic field produced at the point O due to current flowing in an infinite wire shaped as shown in the figure is
 View Solution
View SolutionFind the direction of magnetic field at a point P due to two infinite current carrying wires shown in the figure below
 View Solution
View SolutionA current carrying wire is placed along east and west in a magnetic field directed north wards. If the current in the wire is directed east wards, the direction of force on the wire is
View SolutionThe magnetic field in a straight current carrying conductor wire is:
View SolutionMagnitude of magnetic field at a point P due to a current carrying wire, starting from origin and expanded to y-axis is
View Solution

