A current of 10A flows around a closed path in a circuit which is in the horizontal plane as shown in the figure. The circuit consists oi eight alternating arcs of radii r1=0.08m and r2=0.12m. Each subtends the same angle at the centre.
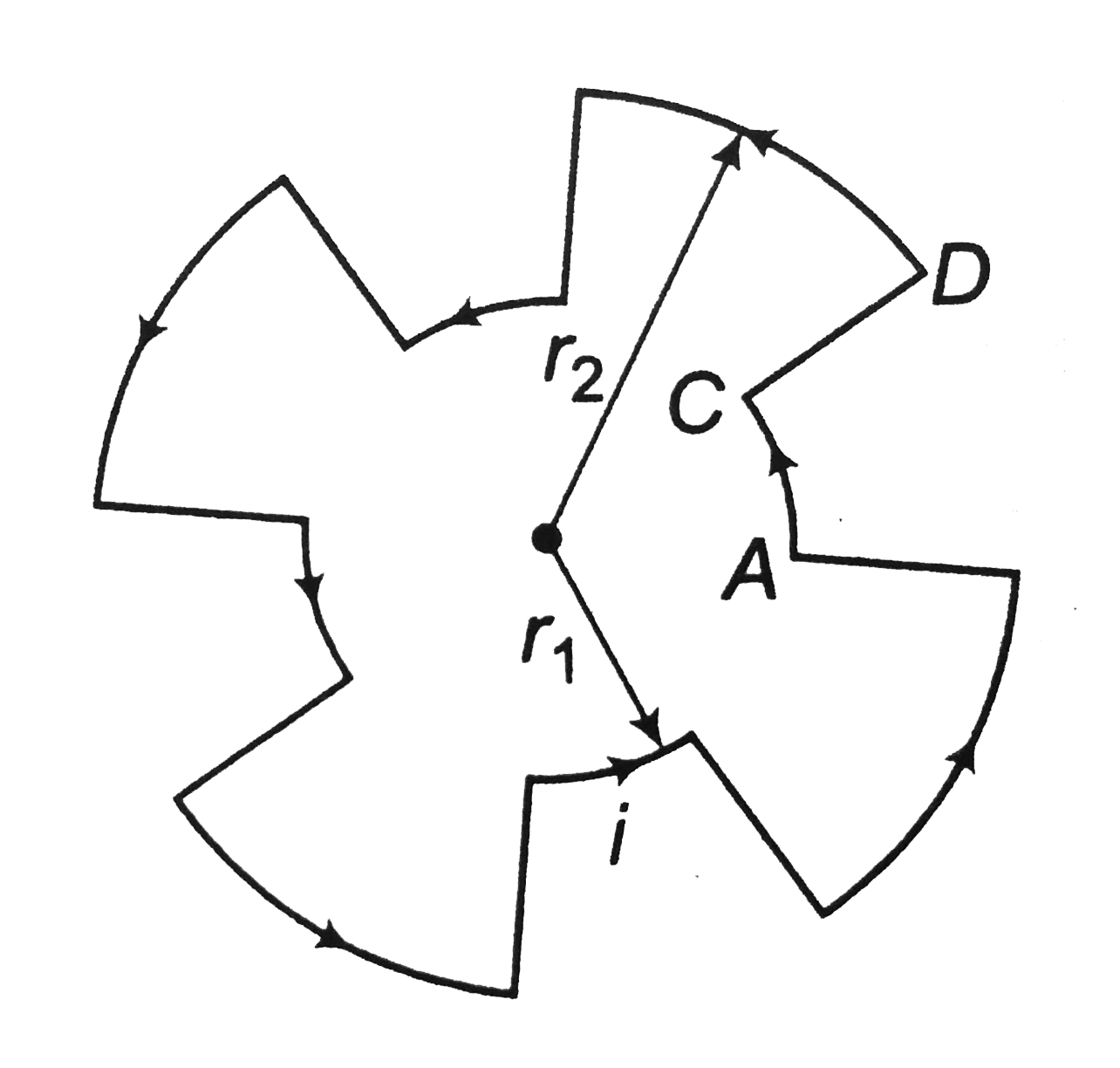
a. Find the magnetic field produced by this circuit at the centre.
b. An infinitely long straight wire carrying as current of 10A is passing through the centre of the above circuit vertically with the direction of the current being into the pane of the circuit. what is the force acting on the wire at the centre due to the current in the circuit? What is the force acting on the arc AC and the straight segment CD due to the current at the centre?
The correct Answer is:(i) 6.54 (ii) (0, 8.1)
(i) 6.54 (ii) (0,8.1)
(i) Given i=10A,r1=0.08m and r2=0.12m. Straight portion i.e. CD etc., will produce zero magnetic field at the centre. Rest eight arcs will produce the magnetic field at the centre in the same direction i.e., perpendicular to the paper outwards or vertically upwards and its magnitude is
B=Binnerarcs+Bouterarcs
=12{μ0i2r1}+12{μ0i2r2}=(μ04π)(πi)(r1+r2r1r2)
Substituting the values we have
B=(10−7)(3.14)(10)(0.08+0.12)(0.08×0.12)
B=6.54×10−5T
(vertically upward or outward normal to the paper)
(ii) Force on AC
Force on circular portions of the circuit i.e., AC etc, due to the wire at the centre will be zero because magnetic field due to the central wire at these arcs will be tangential θ=180∘.
Force on CD
Current in central wire is also i=10A. Magnetic field at distance x due to central wire
B=μ02π.ix∴ Magnetic force on element dx due to this magnetic field
dF=(i)(μ02π.ix).dx=(μ02πi2dxx,(F=ilBsin90∘)
Therefore net force on CD is
F=∫x=r2x=r1dF=μ0i22π∫0.120.08dxx=μ02πi2In(32)
Substituting the values F=(2×10−7)(10)2In(1.5) or F=8.1×10−6N (in wards)
Force on wire at the centre, Net on wire at the centre
Net magnetic field at the centre due to the circuit is in vertical direction and current in the wire in centre is also in vertical direction. Therefore, net force on the wire at the centre will be zero. (θ=180∘). Hence,
(i) force acting on the wire at the centre is zero (ii) force on arc AC=0
(iii) force on segment CD is 8.1×10−6N (inwards)
Topper's Solved these Questions
- BOOK - VMC MODULES ENGLISHCHAPTER - MAGNETIC EFFECTS OF CURRENT EXERCISE - JEE Main (Archive)75videos
MAGNETIC EFFECTS OF CURRENT
- BOOK - VMC MODULES ENGLISHCHAPTER - LIQUIDSEXERCISE - JEE ADVANCED (LEVEL -2)55videos
LIQUIDS
- BOOK - VMC MODULES ENGLISHCHAPTER - MOCK TEST 1EXERCISE - PART I : PHYSICS (SECTION-2)10videos
MOCK TEST 1
Similar Questions
A current of 10 A flow around a closed path in a circuit which is in the horizontal plane as shown in the figure. The circuit consists of eight alternative arcs of radii r1=0.08m and r2=0.12m . Each subtends the same angle at the centre. If magnetic field at centre produced by this circuit is η×10−5T, then the value of η is ?
View SolutionFind the current through resistor R.
 View Solution
View SolutionIn the circuit shown in figure current in the circuit is
 View Solution
View SolutionSwitch is closed at t=0 then the current in the circuit at t=L2R is
_PHY_E06_157_Q01.png) View Solution
View SolutionThe magnetic field strength at a point P distant r due to an infinite straight wire carrying a current i is as shown in the figure
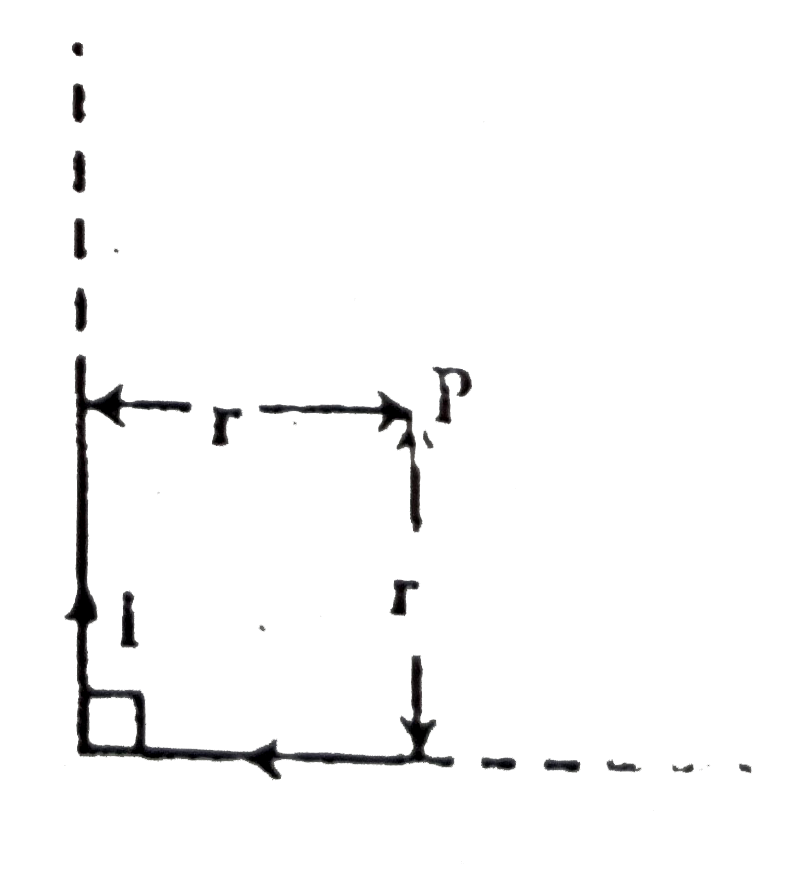 View Solution
View SolutionThe current in the resistor R3 in the circuit as shown in the figure is
 View Solution
View SolutionA piece of wire carrying a current of 6.00 A is bent in the form of a circular arc of radius 10.0 cm, and it subtends an angle of 120∘ at the centre. Find the magnetic field B due to this piece of wire at the centre.
View SolutionFind the current ( in ampere) through wire XY of the circuit shown in figure.
 View Solution
View SolutionAn L-R circuit has a cell of e.m.f. E , which is switched on at time t = 0. The current in the circuit after a long time will be
View SolutionA long straight wire is bent as shown below. Find the resultant magnetic field B at the centre C of the circular path of radius 2 cm if a current I of 5A is passed through the wire.
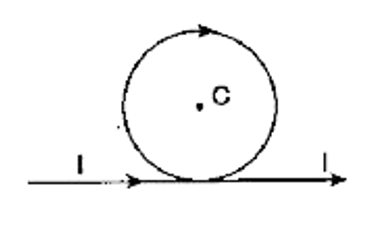 View Solution
View Solution

