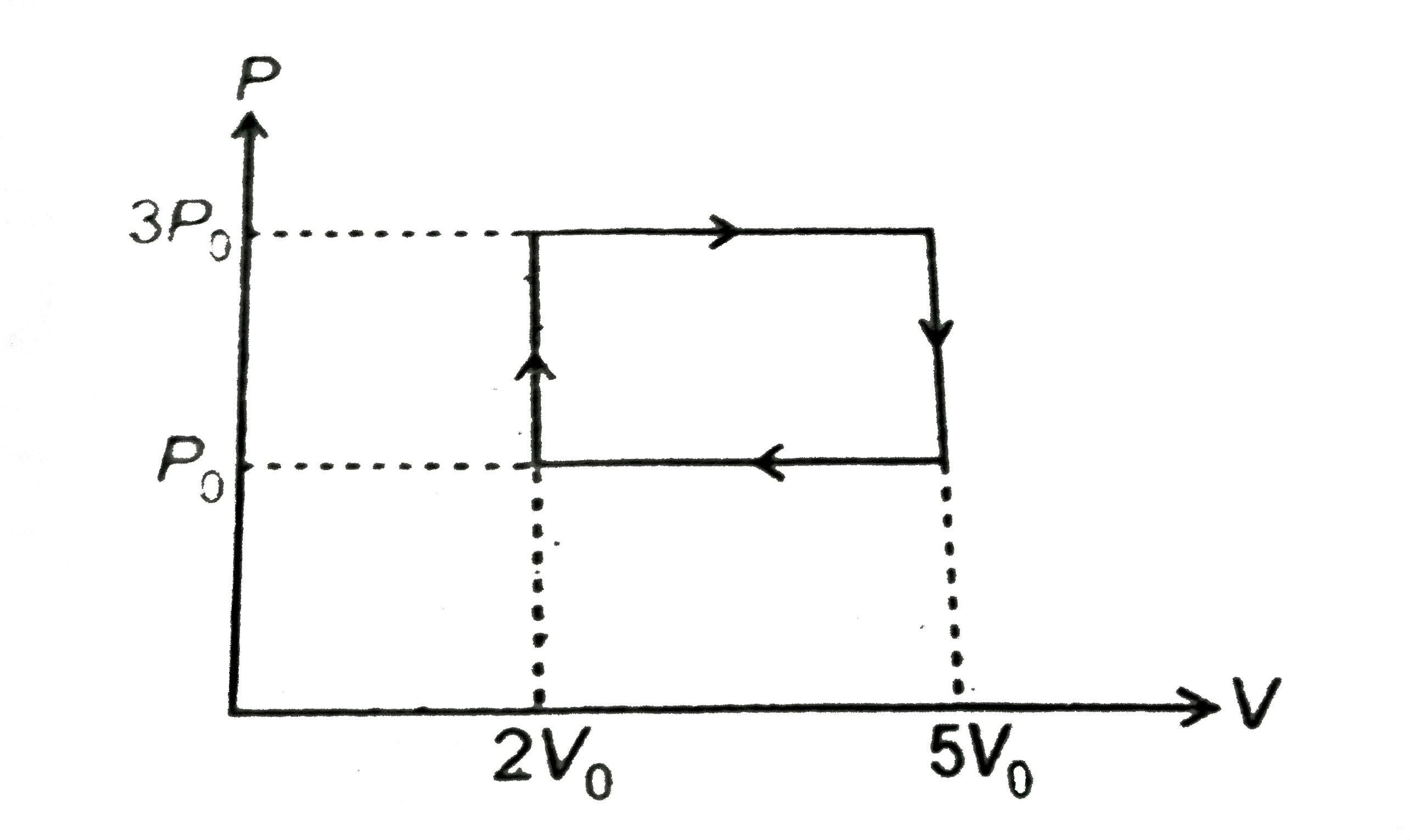
Consider the following cyclic process.
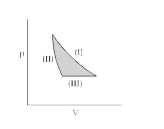
I. Isothermal , II. Adiabatic , (III) constant pressure process
Sum of the work and heat in the above is:
zero
pV
R
−pV
The correct Answer is:A
ΔU=q+wW=0 for cyclic process
Topper's Solved these Questions
- THERMODYNAMICSBOOK - VMC MODULES ENGLISHCHAPTER - THERMODYNAMICSEXERCISE - LEVEL-2
50 Videos
- THERMODYNAMICSBOOK - VMC MODULES ENGLISHCHAPTER - THERMODYNAMICSEXERCISE - LEVEL-2 (NUMERICAL VALUE TYPE)
15 Videos
- THERMODYNAMICSBOOK - VMC MODULES ENGLISHCHAPTER - THERMODYNAMICSEXERCISE - LEVEL-0 (LONG ANSWER TYPE (5 MARKS))
6 Videos
- THERMOCHEMISTRYBOOK - VMC MODULES ENGLISHCHAPTER - THERMOCHEMISTRYEXERCISE - JEE ADVANCED (ARCHIVE)
31 Videos
- THERMODYNAMICS & THERMOCHEMISTRYBOOK - VMC MODULES ENGLISHCHAPTER - THERMODYNAMICS & THERMOCHEMISTRYEXERCISE - Impeccable
48 Videos
Similar Questions
Knowledge Check
Consider a cycle followed by an engine, (figure)
1 to 2 is isothermal 2 to 3 is adiabatic 3 to 1 is adiabatic
such a process does not exist because
Aheat is completely converted to mechanical energy in such a process which is not possibleBmechanical energy is completely converted to heat in this process, which is not possibleCcurves representing two adiabatic processes can intersectDcurves representing an adiabatic process and an isothermal process don't intersect
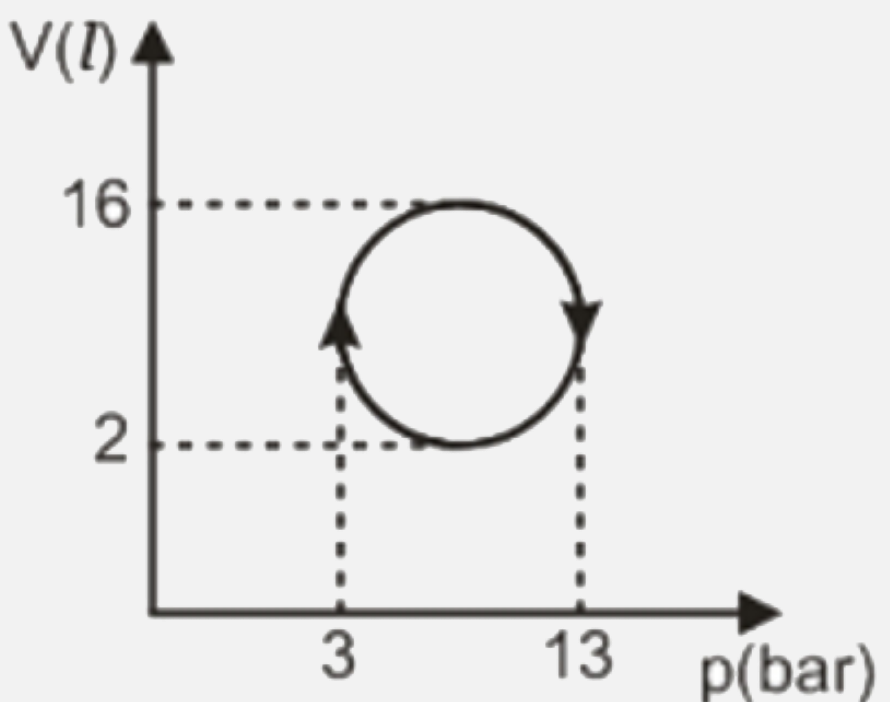
Work done (in kJ) by the gas in the following cyclic process is
View SolutionThe internal energy of a system remains constant when it undergoes
(i) a cyclic process
(ii) an isothermal process
(iii) an adiabatic process
(iv) any process in which the heat given out by the system equal to the work done on the system
View SolutionIsothermal and adiabatic process are identical.
View SolutionIn the following cyclic process is
The above process in the P-T coordinates is given as
View SolutionAn ideal gas undergoes isothermal expansion at constant pressure . During the process.
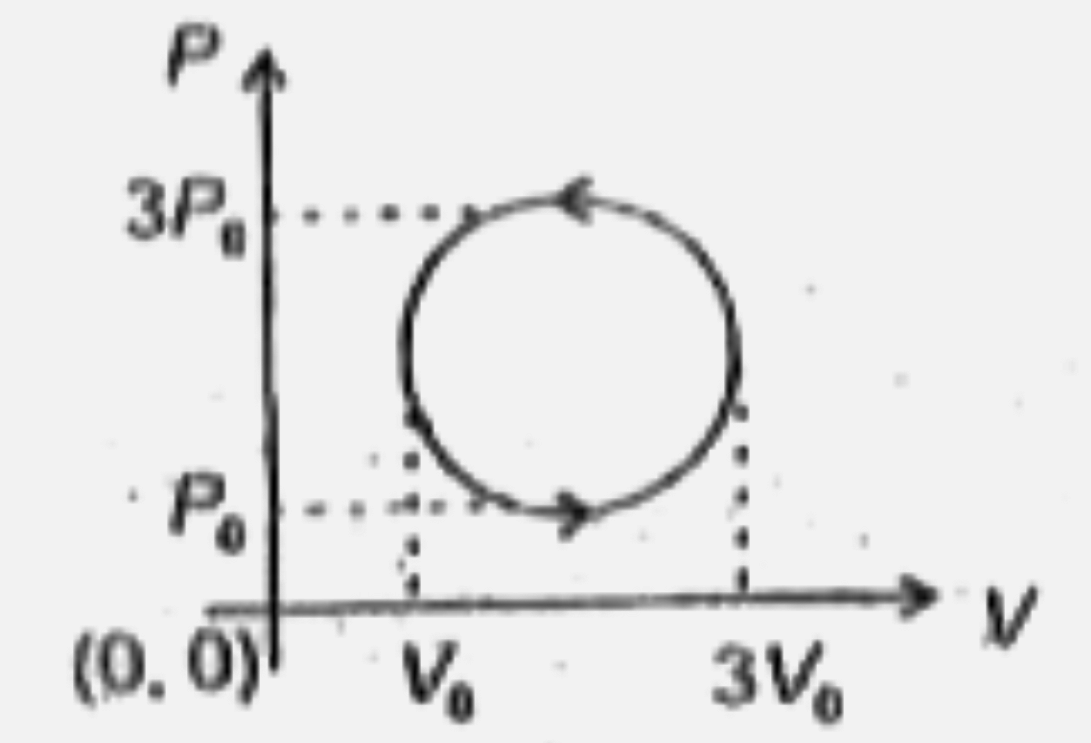
View SolutionWork done in the cyclic process shown in figure is
View SolutionConsider a cycle followed by an engine (figure.)
1 or 2 is isothermal
2 to 3 is adiabatic
3 to 1 is adiabatic
Such a process does not exist, because
View Solution