An unknown resistance R is connected in series with a 2 ohm resistance. A current is flowing in this combination. The balancing length for potential difference across 2 ohm resistor, in a potentiometer experiment is found to be 300 cm, while the balancing length for the potential difference across the unknown R is found to be 360cm. The unknown resistance R is
2.4ohm
3.0 ohm
3.6 ohm
6.6 ohm
To find the unknown resistance R connected in series with a 2-ohm resistor, we can use the relationship between the potential difference across a resistor and the balancing length in a potentiometer experiment. Here’s how to solve the problem step by step:
Step 1: Understand the relationship
In a potentiometer, the potential difference V across a resistor is directly proportional to the balancing length L. This can be expressed as:
V∝L
For resistors in series, the current I is the same through both resistors.
Step 2: Set up the equations
Let’s denote:
- V1 as the potential difference across the 2-ohm resistor,
- V2 as the potential difference across the unknown resistance R.
From the problem statement:
- The balancing length for the 2-ohm resistor is 300 cm.
- The balancing length for the unknown resistance R is 360 cm.
Using the proportionality, we can write:
V1=I⋅2(for the 2-ohm resistor)
V2=I⋅R(for the unknown resistor)
Step 3: Write the equations based on the lengths
From the balancing lengths, we can relate the voltages to the lengths:
V1V2=L1L2
Substituting the known values:
I⋅2I⋅R=300360
Step 4: Simplify the equation
The current I cancels out:
2R=300360
Now, simplify the right side:
300360=56
So we have:
2R=56
Step 5: Cross-multiply to solve for R
Cross-multiplying gives:
2⋅6=5⋅R
12=5R
Step 6: Solve for R
Now, divide both sides by 5:
R=125=2.4ohms
Final Answer
The unknown resistance R is 2.4ohms.
---
In a potentiometer, the potential difference V across a resistor is directly proportional to the balancing length L. This can be expressed as:
V∝L
For resistors in series, the current I is the same through both resistors.
Let’s denote:
- V1 as the potential difference across the 2-ohm resistor,
- V2 as the potential difference across the unknown resistance R.
- The balancing length for the 2-ohm resistor is 300 cm.
- The balancing length for the unknown resistance R is 360 cm.
V1=I⋅2(for the 2-ohm resistor)
V2=I⋅R(for the unknown resistor)
From the balancing lengths, we can relate the voltages to the lengths:
V1V2=L1L2
Substituting the known values:
I⋅2I⋅R=300360
The current I cancels out:
2R=300360
Now, simplify the right side:
300360=56
So we have:
2R=56
Cross-multiplying gives:
2⋅6=5⋅R
12=5R
Now, divide both sides by 5:
R=125=2.4ohms
The unknown resistance R is 2.4ohms.
Topper's Solved these Questions
- BOOK - VMC MODULES ENGLISHCHAPTER - DC CIRCUITEXERCISE - LEVEL-2 DAILY TUTORIAL SHEET-410videos
DC CIRCUIT
- BOOK - VMC MODULES ENGLISHCHAPTER - DC CIRCUITEXERCISE - LEVEL-2 DAILY TUTORIAL SHEET-510videos
DC CIRCUIT
- BOOK - VMC MODULES ENGLISHCHAPTER - DC CIRCUITEXERCISE - LEVEL-2 DAILY TUTORIAL SHEET-210videos
DC CIRCUIT
- BOOK - VMC MODULES ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - IN-CHAPTER EXERCISE-F10videos
CURRENT ELECTRICITY
- BOOK - VMC MODULES ENGLISHCHAPTER - DYNAMICS OF A PARTICLEEXERCISE - JEE Advance (Archive) Level - II (SINGLE OPTION CORRECT TYPE )31videos
DYNAMICS OF A PARTICLE
Similar Questions
In a potential meter arrangement shown in fig. The balancing length for potential difference across X,Y points is found to be 45.5 cm. Then the balancing length for potential difference across ( Y ) and ( Z) would be
 View Solution
View SolutionAccording to this diagram , the potential difference across the terminals is ( internal resistance of cell =r)
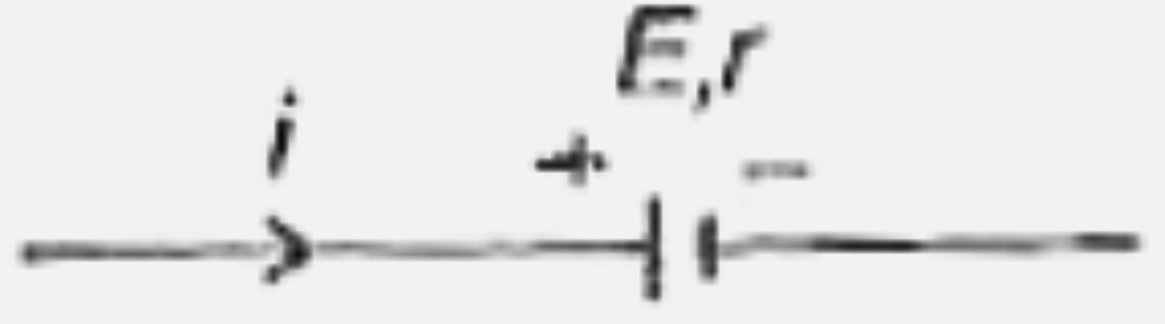 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A cell having an emf E and internal resistance r is connected across a variable external resistance R. As the resistance R is increased, the plot of potential difference V across R is given by
A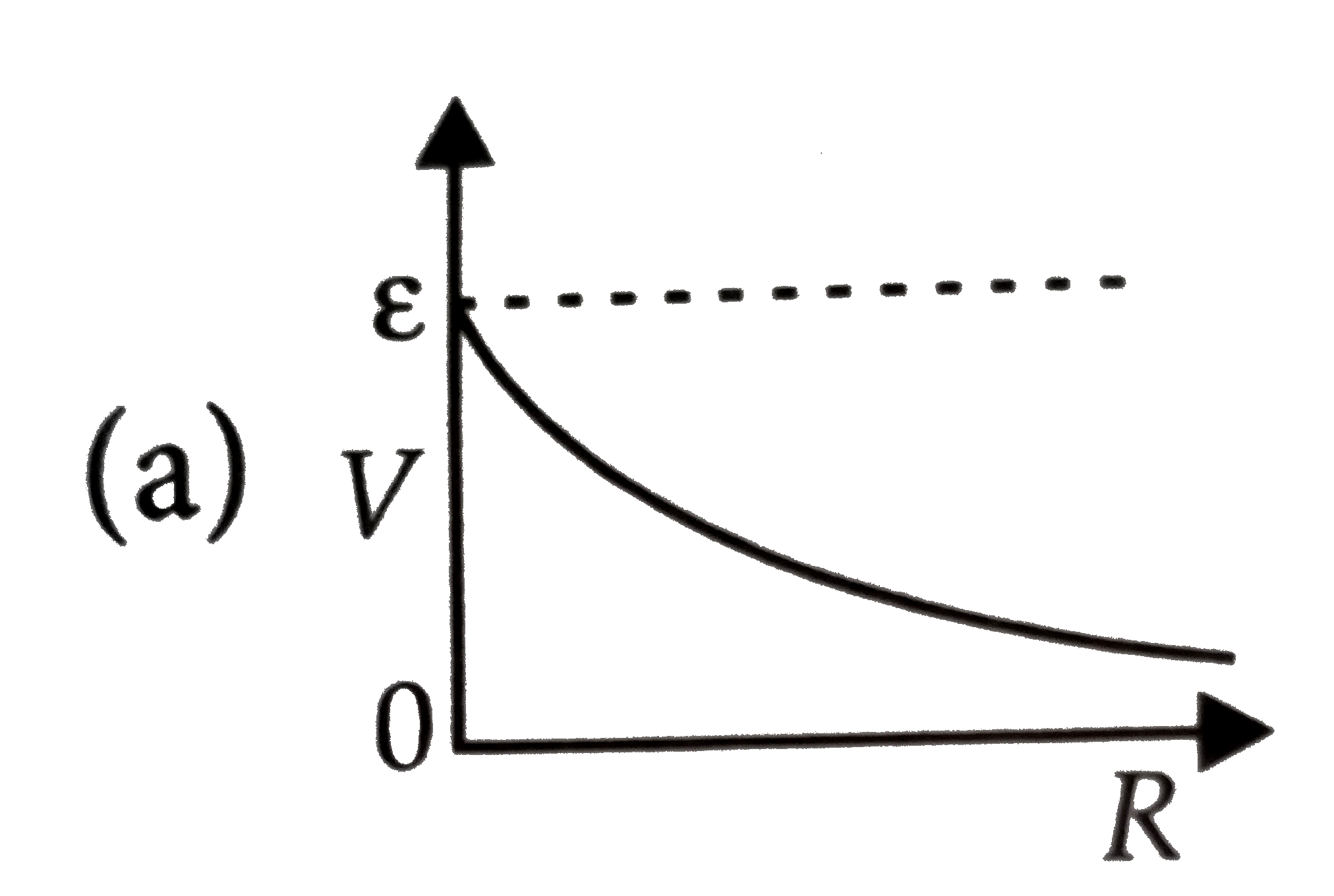 B
B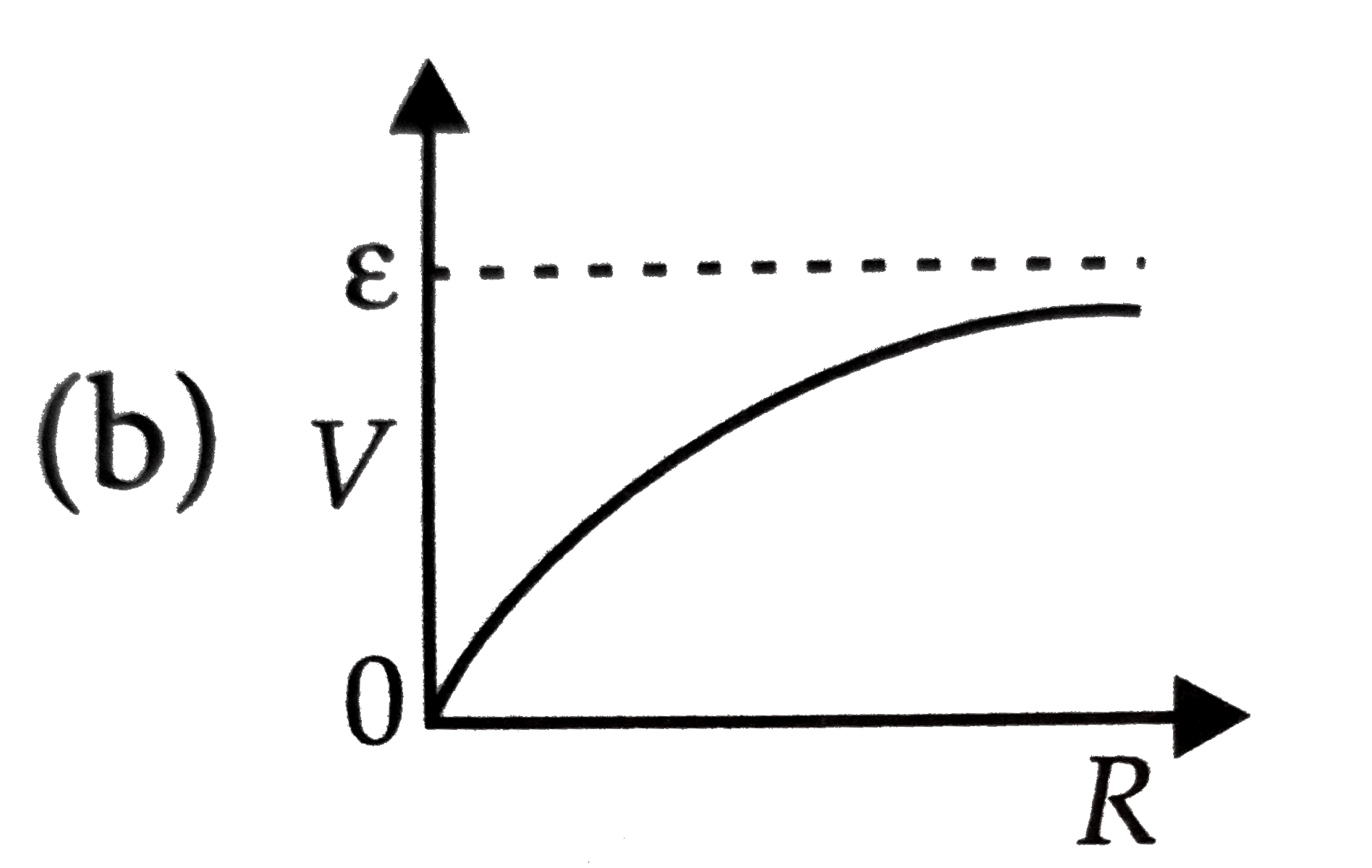 C
C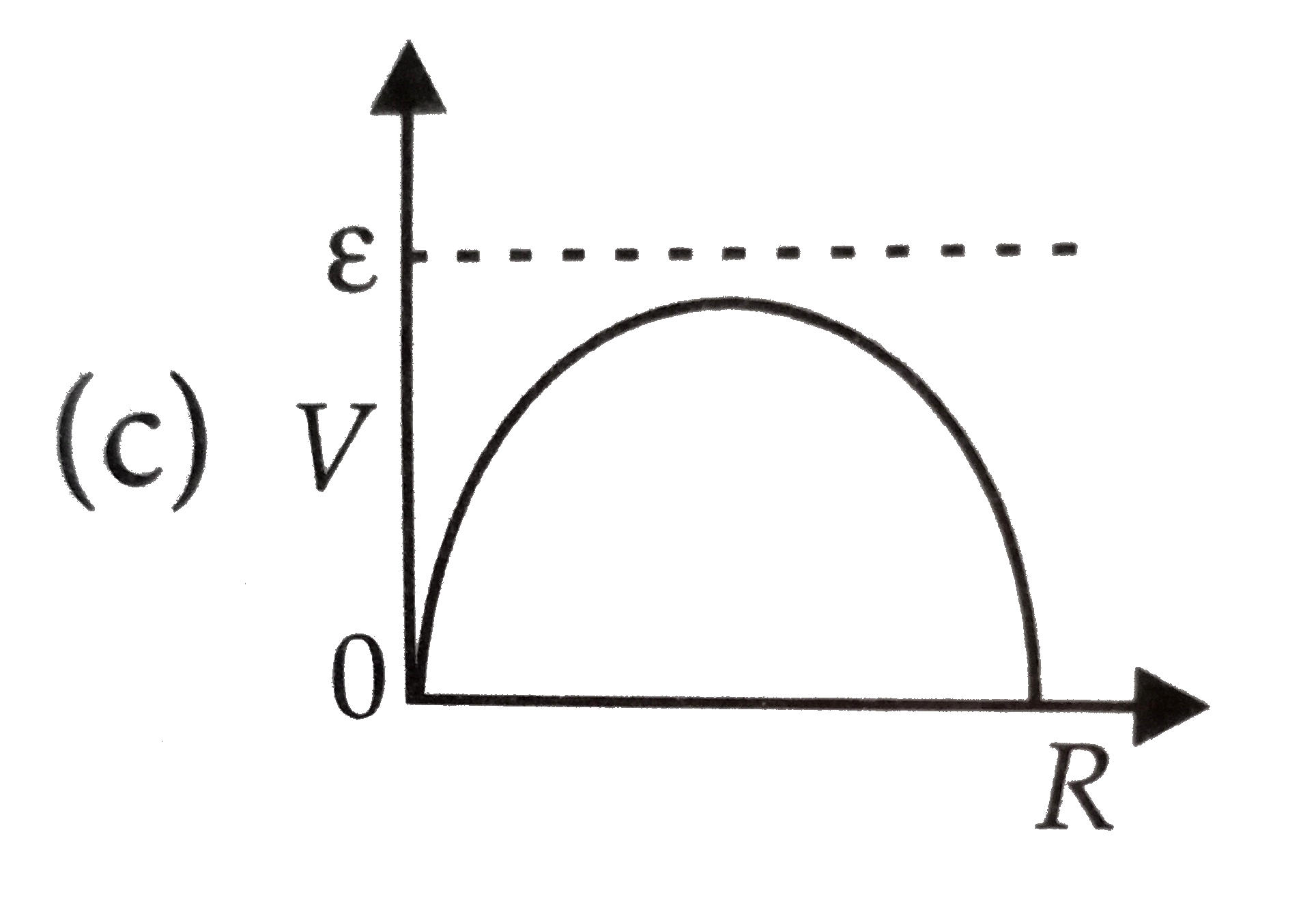 D
D
In the given circuit, if the potential difference across the internal resistance r1 is equal to E, then the resistance R is equal to:
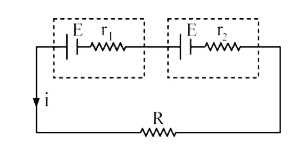 View Solution
View SolutionA cell having an emf E and internal resistance r is connected across a variable external resistance R. As the resistance R is increased, the plot of potential difference V across R is given by
View SolutionIf the resistance of potentiometer wire is 15r then calculate the balance length l
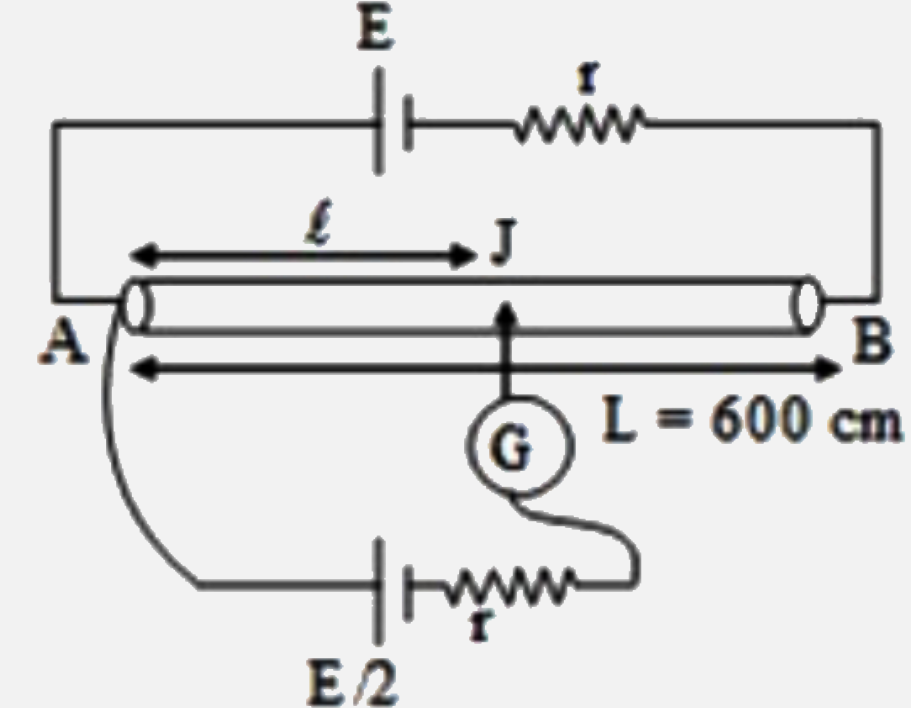 View Solution
View SolutionIn a network as shown in the figure , the potential difference across the resistance 2 R is (the cell has emf E - volt and no internal resistance )
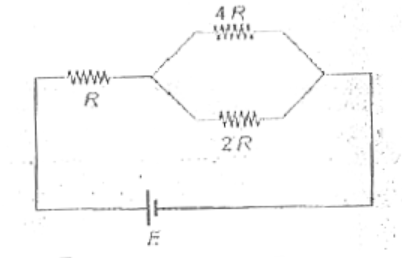 View Solution
View SolutionIn a potentiometer experiment, the balancing length with a resistance of 2Ω is found to be 100cm, while that of an unknown resistance is 500cm. Calculate the value of the unknown resistance.
View SolutionThe potential gradient of potentiometer is 0.2volt/m. A current of 0.1 amp is flowing throgh a coil of 2 ohm resistance. The balancing length in meters for the potential difference at the ends of this coil will be
View SolutionA resistor R is connected to a cell of emf e and internal resistance r. Potential difference across the resistor R is found to be V. State the relation between e, V, R and r.
View Solution

