A uniform wire of resistance R is slaped into a regular n-sided polygon (n is seven). The equivalent resistance between any two corners can have :
the maximum valueR/4
the maximum value R/n
the value of equivalent resistance is R(n−1n2)
the minimum value R/n
To find the equivalent resistance between any two corners of a regular 7-sided polygon formed by a uniform wire of resistance R, we can follow these steps:
Step 1: Understand the Configuration
A regular 7-sided polygon (heptagon) has 7 vertices (corners) and can be thought of as having 7 equal segments of wire, each with a resistance of R7.
Step 2: Identify the Resistance Between Two Corners
When considering the resistance between two adjacent corners (let's call them corner A and corner B), the wire segment directly connecting them has a resistance of R7.
Step 3: Calculate the Resistance for Non-Adjacent Corners
For non-adjacent corners, we need to consider the paths available. For example, if we want to find the equivalent resistance between corner A and corner C (two corners apart), we have two paths:
1. Direct path from A to B (resistance R7) and then from B to C (resistance R7).
2. The longer path that goes around the other way (A to G to F to E to D to C).
Step 4: Use the Formula for Equivalent Resistance
For the equivalent resistance Req between any two corners, we can use the formula for resistors in parallel and series. The formula for the equivalent resistance Req between two corners in an n-sided polygon is given by:
Req=(n−1)Rn2
Step 5: Substitute n=7
Now substituting n=7 into the formula:
Req=(7−1)R72=6R49
Conclusion
Thus, the equivalent resistance between any two corners of a regular 7-sided polygon formed by a uniform wire of resistance R is:
Req=6R49
A regular 7-sided polygon (heptagon) has 7 vertices (corners) and can be thought of as having 7 equal segments of wire, each with a resistance of R7.
When considering the resistance between two adjacent corners (let's call them corner A and corner B), the wire segment directly connecting them has a resistance of R7.
For non-adjacent corners, we need to consider the paths available. For example, if we want to find the equivalent resistance between corner A and corner C (two corners apart), we have two paths:
1. Direct path from A to B (resistance R7) and then from B to C (resistance R7).
2. The longer path that goes around the other way (A to G to F to E to D to C).
For the equivalent resistance Req between any two corners, we can use the formula for resistors in parallel and series. The formula for the equivalent resistance Req between two corners in an n-sided polygon is given by:
Now substituting n=7 into the formula:
Thus, the equivalent resistance between any two corners of a regular 7-sided polygon formed by a uniform wire of resistance R is:
Topper's Solved these Questions
- BOOK - VMC MODULES ENGLISHCHAPTER - DC CIRCUITEXERCISE - LEVEL-2 DAILY TUTORIAL SHEET-510videos
DC CIRCUIT
- BOOK - VMC MODULES ENGLISHCHAPTER - DC CIRCUITEXERCISE - LEVEL-1 JEE MAIN ARCHIVE93videos
DC CIRCUIT
- BOOK - VMC MODULES ENGLISHCHAPTER - DC CIRCUITEXERCISE - LEVEL-2 DAILY TUTORIAL SHEET-310videos
DC CIRCUIT
- BOOK - VMC MODULES ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - IN-CHAPTER EXERCISE-F10videos
CURRENT ELECTRICITY
- BOOK - VMC MODULES ENGLISHCHAPTER - DYNAMICS OF A PARTICLEEXERCISE - JEE Advance (Archive) Level - II (SINGLE OPTION CORRECT TYPE )31videos
DYNAMICS OF A PARTICLE
Similar Questions
A uniform metallic wire has a resistance of 18 Ω and is bent into an equiolateral triangle. Then, the resistance between any two vertices of the triangle is :
View SolutionA wire of resistance 15.0(Ω)is bent to form a regular hexagon ABCDEFA.Find the equivalent resistance of the loop between the points (a)A and B, (b)A and C and (c )A and D .
View SolutionA frame is formed by nine identical wires of resistances R each as shown in the figure.
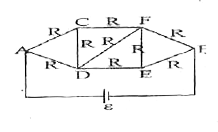
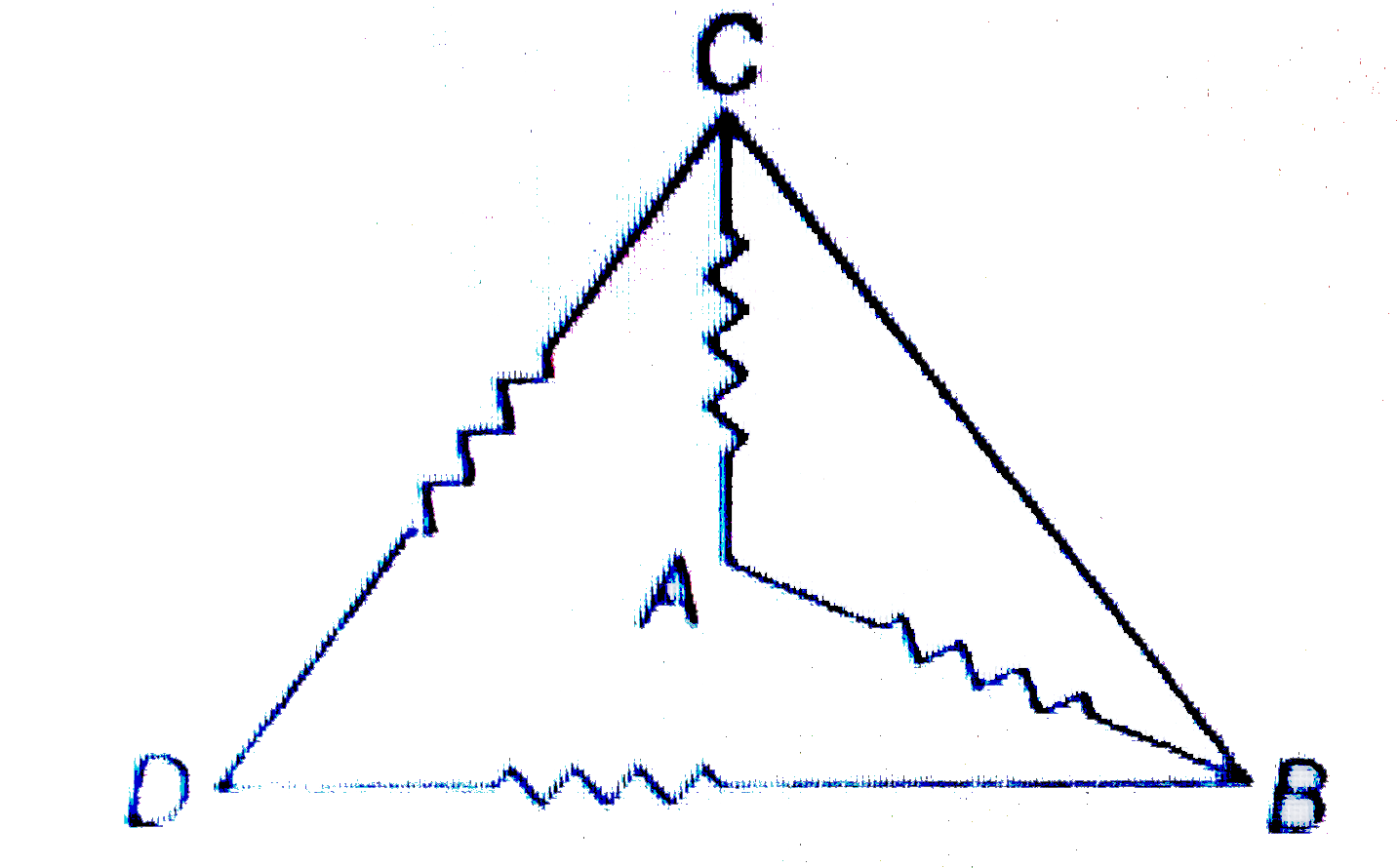
The equivalent resistance between A and B isView SolutionEach resistance of the circuit shown in figure is r. The equivalent resistance between A and B is
 View Solution
View SolutionA wire of resistance 15.0(Ω)is bent to form a regular hexagon ABCDEFA.Find the equivalent resistance of the loop between the points (a)A and B, (b)A and C and (c )A and D .
View SolutionA wire has a resistance of 12 ohm . It is bent in the form of equilateral triangle. The effective resistance between any two corners of the triangle is
View SolutionSeven resistance are connected as shown in the firgure. The equivalent resistance between A and B is
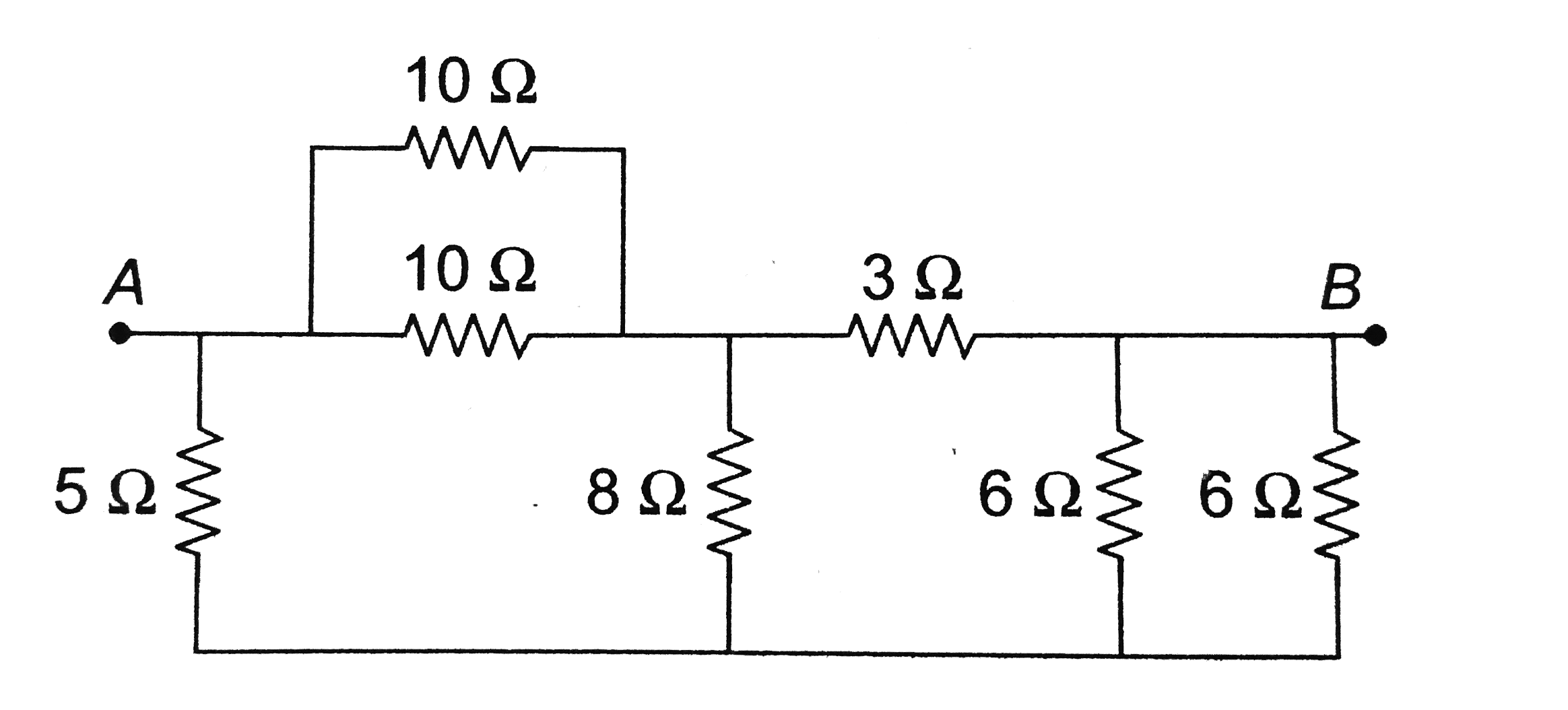 View Solution
View SolutionFour identical resistances each having value R are arranged as shown in Figure. Find the equivalent resistance between A and B.
 View Solution
View Solutionfind the equivalent resistance between A and E(resistance of each resistor is R.
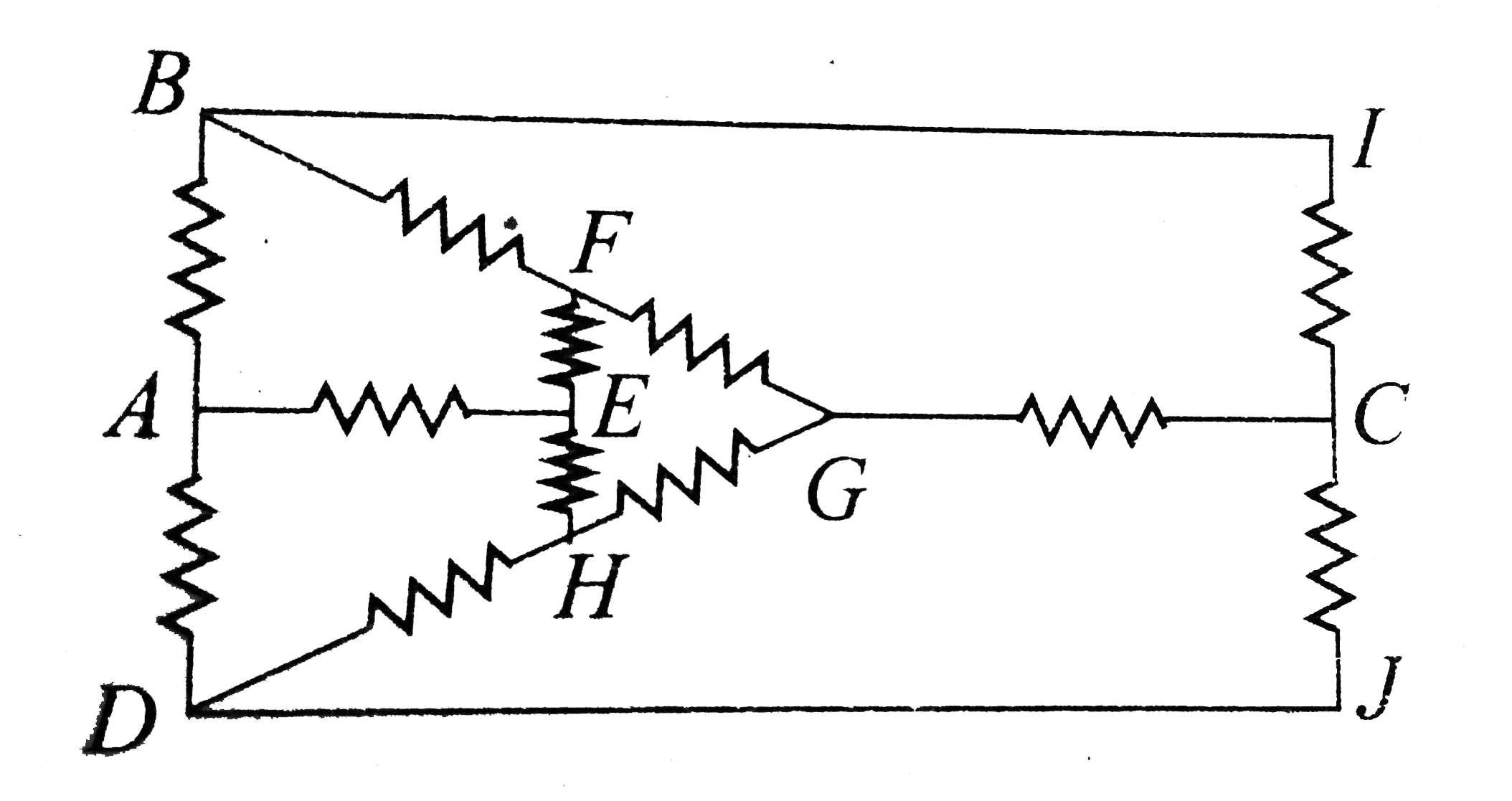 View Solution
View SolutionIn the network shown in fig. each resistance is R.

The equivalent resistance between A and C isView Solution

