The densitis of two solid spheres A and B of the same radii R very with radial distance respectively, where k is a constant . The moments of inertia of the inividual spheres about axes passing throgh their centres are respectively. if the value of n is
To solve the problem, we need to find the ratio of the moments of inertia of two solid spheres A and B with varying densities. The densities are given as:
- For sphere A: pA(r)=k(rR)
- For sphere B: pB(r)=k(rR5)
Step 1: Calculate the mass of a thin shell for both spheres
For a thin spherical shell of radius r and thickness dr:
- The volume of the shell is dV=4πr2dr.
For sphere A:
- The mass of the thin shell is:
dmA=pA(r)⋅dV=k(rR)⋅4πr2dr=4πkr3Rdr
For sphere B:
- The mass of the thin shell is:
dmB=pB(r)⋅dV=k(rR5)⋅4πr2dr=4πkr3R5dr
Step 2: Calculate the moment of inertia for both spheres
The moment of inertia dI of a thin shell is given by:
dI=r2dm
For sphere A:
dIA=r2⋅dmA=r2⋅4πkr3Rdr=4πkr5Rdr
To find the total moment of inertia IA, integrate from 0 to R:
IA=∫R04πkr5Rdr=4πkR(r66)R0=4πkR56R=2πkR53
For sphere B:
dIB=r2⋅dmB=r2⋅4πkr3R5dr=4πkr5R5dr
To find the total moment of inertia IB, integrate from 0 to R:
IB=∫R04πkr5R5dr=4πkR5(r66)R0=4πkR5⋅R66=2πkR3
Step 3: Find the ratio of the moments of inertia
Now we can find the ratio IBIA:
IBIA=2πkR32πkR53=RR5=1R4
Step 4: Relate the ratio to n10
According to the problem statement:
IBIA=n10
Setting the two expressions equal gives:
1R4=n10
Thus, we can solve for n:
n=10R4
Step 5: Determine the value of n
Since the problem states that n is a constant, we can assume R=1 for simplicity, leading to:
n=10
Conclusion
Thus, the value of n is 6.
---
- For sphere B: pB(r)=k(rR5)
- The volume of the shell is dV=4πr2dr.
- The mass of the thin shell is:
dmA=pA(r)⋅dV=k(rR)⋅4πr2dr=4πkr3Rdr
- The mass of the thin shell is:
dmB=pB(r)⋅dV=k(rR5)⋅4πr2dr=4πkr3R5dr
dI=r2dm
dIA=r2⋅dmA=r2⋅4πkr3Rdr=4πkr5Rdr
To find the total moment of inertia IA, integrate from 0 to R:
IA=∫R04πkr5Rdr=4πkR(r66)R0=4πkR56R=2πkR53
dIB=r2⋅dmB=r2⋅4πkr3R5dr=4πkr5R5dr
To find the total moment of inertia IB, integrate from 0 to R:
IB=∫R04πkr5R5dr=4πkR5(r66)R0=4πkR5⋅R66=2πkR3
IBIA=2πkR32πkR53=RR5=1R4
IBIA=n10
Setting the two expressions equal gives:
1R4=n10
Thus, we can solve for n:
n=10R4
n=10
Topper's Solved these Questions
- BOOK - VMC MODULES ENGLISHCHAPTER - ROTATIONAL MOTION EXERCISE - JEE Advanced (Archive) (FILL IN THE BLANKS TYPE)14videos
ROTATIONAL MOTION
- BOOK - VMC MODULES ENGLISHCHAPTER - ROTATIONAL MOTION EXERCISE - JEE Advanced (Archive) (True/False Type)3videos
ROTATIONAL MOTION
- BOOK - VMC MODULES ENGLISHCHAPTER - ROTATIONAL MOTION EXERCISE - JEE Advanced (Archive) (MATRIX MATCH TYPE)1videos
ROTATIONAL MOTION
- BOOK - VMC MODULES ENGLISHCHAPTER - REVISION TEST-2 JEEEXERCISE - PHYSICS25videos
REVISION TEST-2 JEE
- BOOK - VMC MODULES ENGLISHCHAPTER - SIMPLE HARMONIC MOTION EXERCISE - 7-previous year question46videos
SIMPLE HARMONIC MOTION
Similar Questions
Two circular loops A and B of radii R and 2R respectively are made of the similar wire. Their moments of inertia about the axis passing through the centre of perpendicular to their plane are IA and IB respectively. The ratioIAIB is :
View SolutionTwo loops P and Q are made from a uniform wire. The radii of P and Q are R1 and R2, respectively, and their moments of inertia about their axis of rotation are I1 and I2, respectively. If I1I2=4, then R2R1 is
View Solution
Knowledge Check
- Question 1 - Select One
The radius of gyration of a solid sphere of radius R about a certain axis is also equal to R. If r is the distance between the axis and the centre of the sphere, then r is equal to
ARB0.5RC√0.6RD√0.3R
If two circular discs A and B are of same mass but of radii r and 2r respectively, then the moment of inertia of A is
View SolutionTwo identical capacitors A and B are charged to the same potential and then made to discharge through resistances RA and RB respectively, with RA>RB.
View SolutionThree ammeters A,B, and C of resistances RA,Rb and RC respectively are joined as shown. When some potential difference is appllied across the terminals T1 and T2 their readings are IA,IBandIC respectively Then,
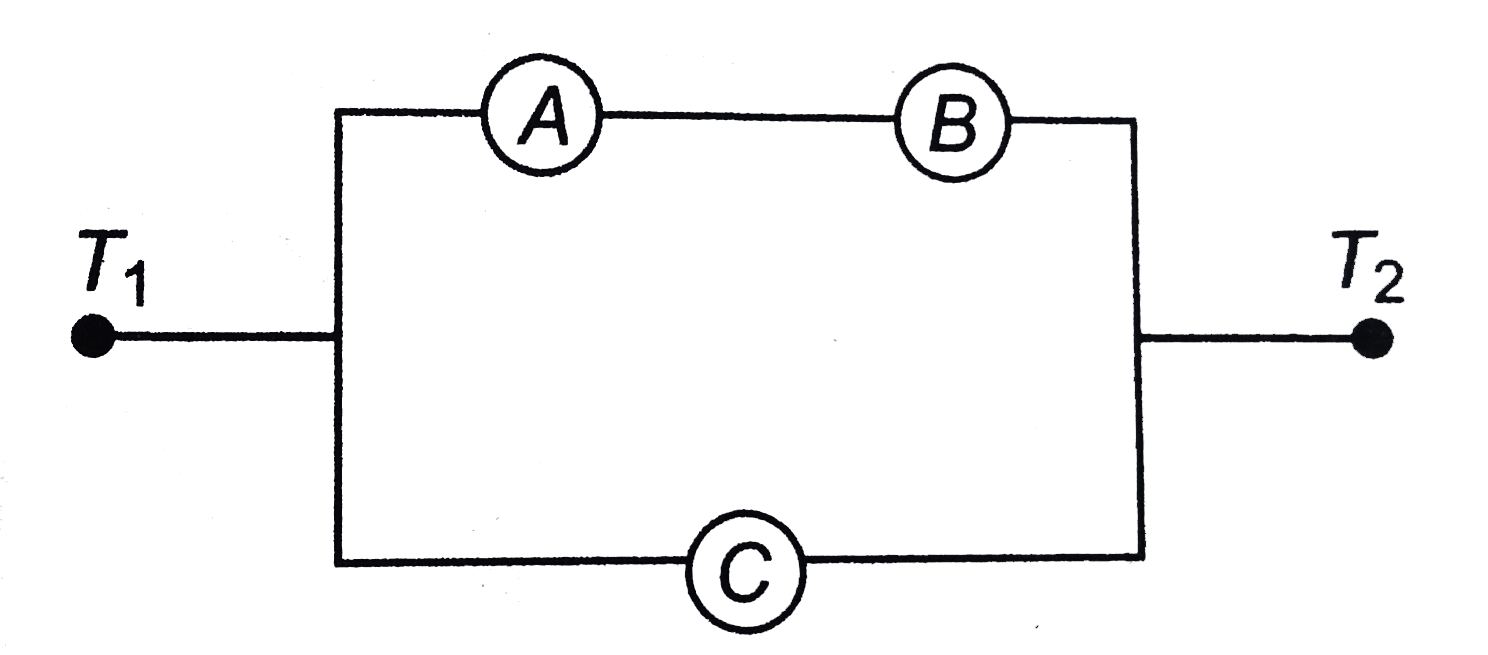 View Solution
View SolutionThe wavelength of Kα X-rays of two metals AandB are4/1875Rand1/675R, respectively , where R is rydberg 's constant. The number of electron lying between AandB according to this lineis
View SolutionThe wavelength of Kα X-rays of two metals AandB are4/1875Rand1/675R, respectively , where R is rydberg 's constant. The number of electron lying between AandB according to this lineis
View SolutionOne solid sphere A and another hollow sphere B are of same mass and same outer radii. Their moment of inertia about their diameters are respectively IA and IB such that.
View SolutionTwo spheres of radii R1 and R1 respectively are charged and joined by wire. The ratio of electric field of spheres is
View Solution

