Three particles A, B and C each of mass m, are connected to each other by three massless rigid rods to form a rigid, equilateral triangular body of side l. This body is placed on a horizontal frictionless table (x-y plane) and is hinged to it at the point A so that it can move without friction about the vertical axis through A . the body is set into rotational motion on the table about A with a constant angular velocity ω.
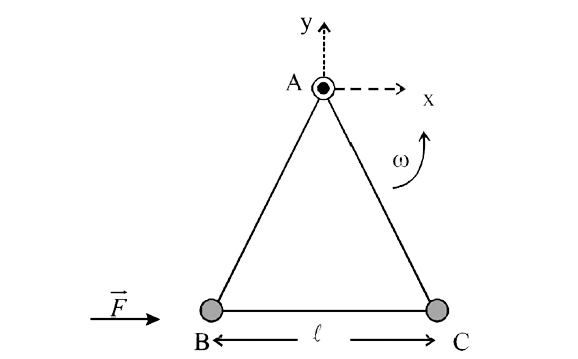
(a) Find the magnitude of the horizontal force exerted by the hinge on the body.
(b) At time T, when the side BC is parallel to the x-axis, a force F is applied on B along BC (as shown). Obtain the x-component and the y-component of the force exerted by the hinge on the body, immediately after time T.
(i) √3mIω2, (ii) FX=F4,FY=√3mIω2
(i) The centre of mass of the system is at the centroid of a triangular assembly. The CM moves along a circular path with constant angular velocity. Therefore, there must be a horizontal centripetal force directed towards the axis at the hinge.
From, figure (a), we find
AD=Isin60∘=I√32
AO=23AD=1√3=r
The centripetal acceleration ac=ω2r=ω2(1√3)
Hinge force, Fb=m(ω21√3)=√3mIω2.

(ii) Let Fx and Fy be the forces applied by the hinges along x-axis and y-axis, respectively.
∑τ=F×(√32l)=2mI2α⇒α=√3F4ml
∑FX=FX+F=(3m)at=3m(1√3α)=3F4⇒FX=F4
∑FY=FY=3m(1√3)ω2=√3mIω2
Topper's Solved these Questions
- ROTATIONAL MOTION BOOK - VMC MODULES ENGLISHCHAPTER - ROTATIONAL MOTION EXERCISE - JEE Advanced (Archive) (True/False Type)
3 Videos
- ROTATIONAL MOTION BOOK - VMC MODULES ENGLISHCHAPTER - ROTATIONAL MOTION EXERCISE - JEE Advanced (Archive) (NUMERICAL VALUE TYPE)
15 Videos
- REVISION TEST-2 JEEBOOK - VMC MODULES ENGLISHCHAPTER - REVISION TEST-2 JEEEXERCISE - PHYSICS
25 Videos
- SIMPLE HARMONIC MOTION BOOK - VMC MODULES ENGLISHCHAPTER - SIMPLE HARMONIC MOTION EXERCISE - 7-previous year question
46 Videos
Similar Questions
Three point masses each of mass'm' are joined together using a string to form an equilateral triangle of side 'a'. The system is placed on a smooth horizontal surface and rotated with a constant angular velocity 'ω' about a vertical axis passing through the centroid. Then the tension in each string is
View SolutionThree particles A,B and C each of mass m are lying at the corners of an equilateral triangle of side L . If the particle A is released keeping the particles B and C fixed , the magnitude of instantaneous acceleration of A is
View SolutionA body of mass 40 gm is moving with a constant velocity of 2cm/sec on a horizontal frictionless table. The force on the table is
View SolutionThe angular velocity of a rigid body about any point of that body is same :
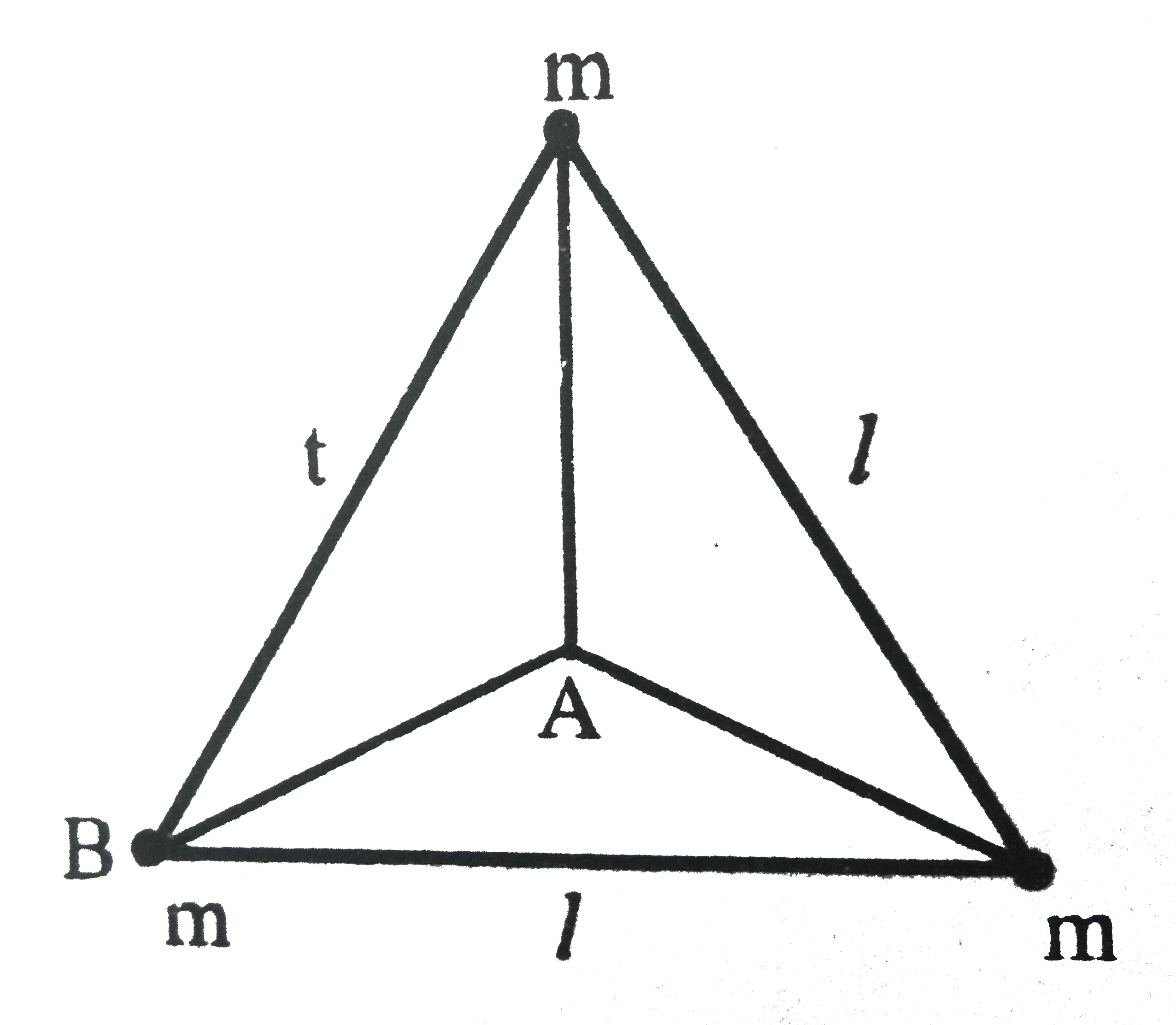
View SolutionThree equal masses m are rigidly connected to each other by massless rods of length l forming and equilateral triangle, as shown above. The assembly is to be given an angular velocity ω about an axis perpendicular to the triangle. For fixed ω, what is the ratio of the kinetic energy of the assembly for an axis through Bt compared with that for an axis through A.
 .
.
View SolutionThree point charges, each with charge q and mass 'm', are connected by three strings of equal length l whose other end is connected to a fixed point P. They form an equilateral triangle of side 'a' in a horizontal plane. The tension in each string will be
View SolutionThree point masses 'm' each are placed at the three vertices of an equilateral traingle of side 'a'. Find net gravitational force on any point mass.
View SolutionThree particle each of mass m are placed at the corners of equilateral triangle of side l

Which of the following is/are correct ?
View SolutionThree particles, each of mass m are situated at the vertices of an equilateral triangle ABC of side L as shown in the figure. Find the moment of inertia of the system about the line AX perpendicular to AB in the plane of ABC
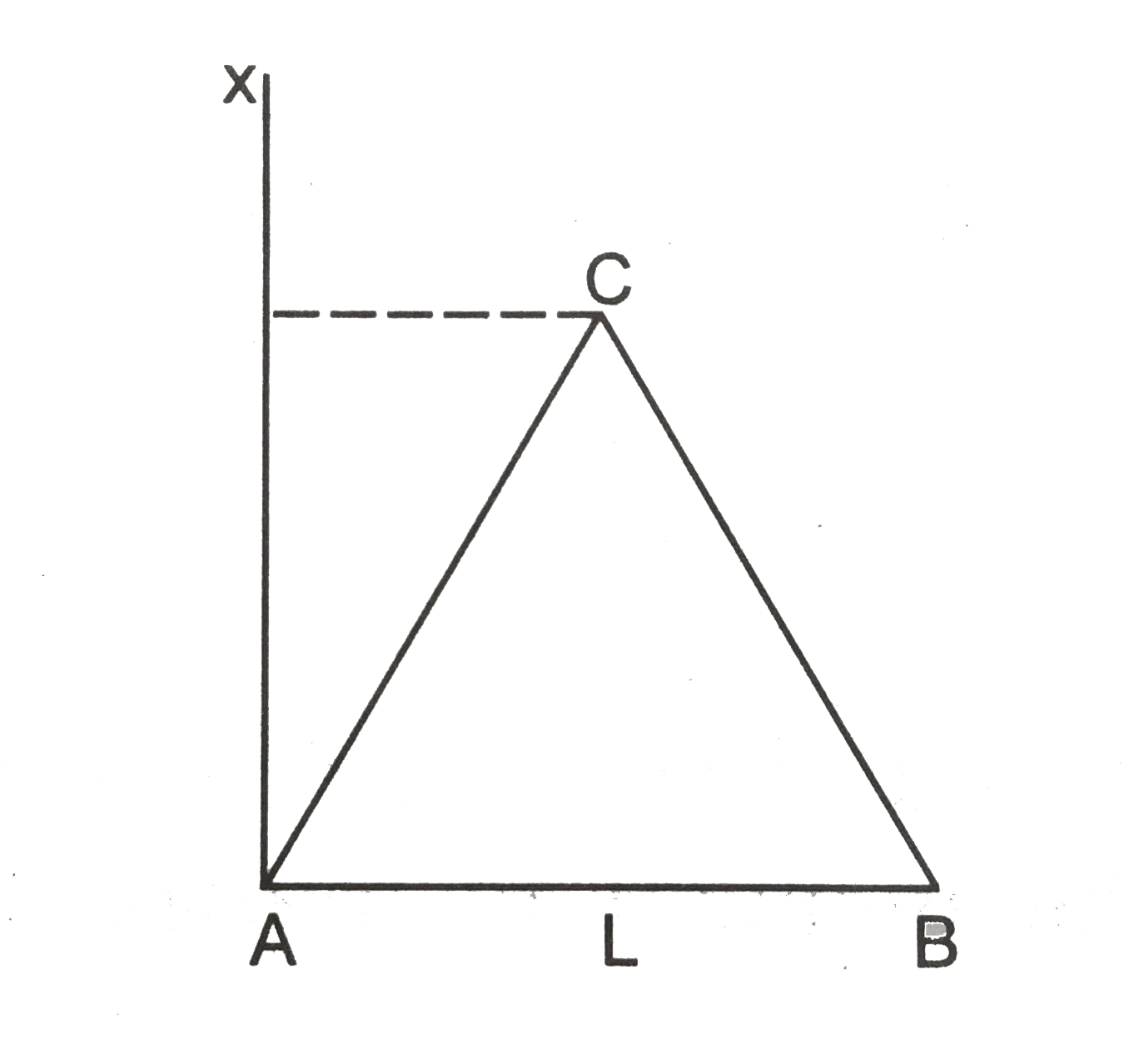
View SolutionThree particles, each of mass m are situated at the vertices of an equilateral triangle ABC of side l (as shown in the figure).
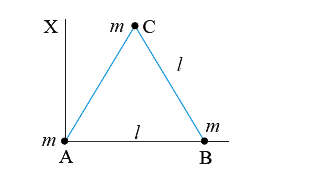
The moment of inertia of the system about a line AX perpendicular to AB and in the plane of ABC, will be:
View Solution
