A uniform disc of mass m and radius r is projected horizontally with velocity v0 on a rough horizontal floor so that it starts off with a purely sliding motion at t=0. At t=t0 seconds it acquires a purely rolling motion.
a. Calculate the velocity of the centre of mass of the disc at t=t0.
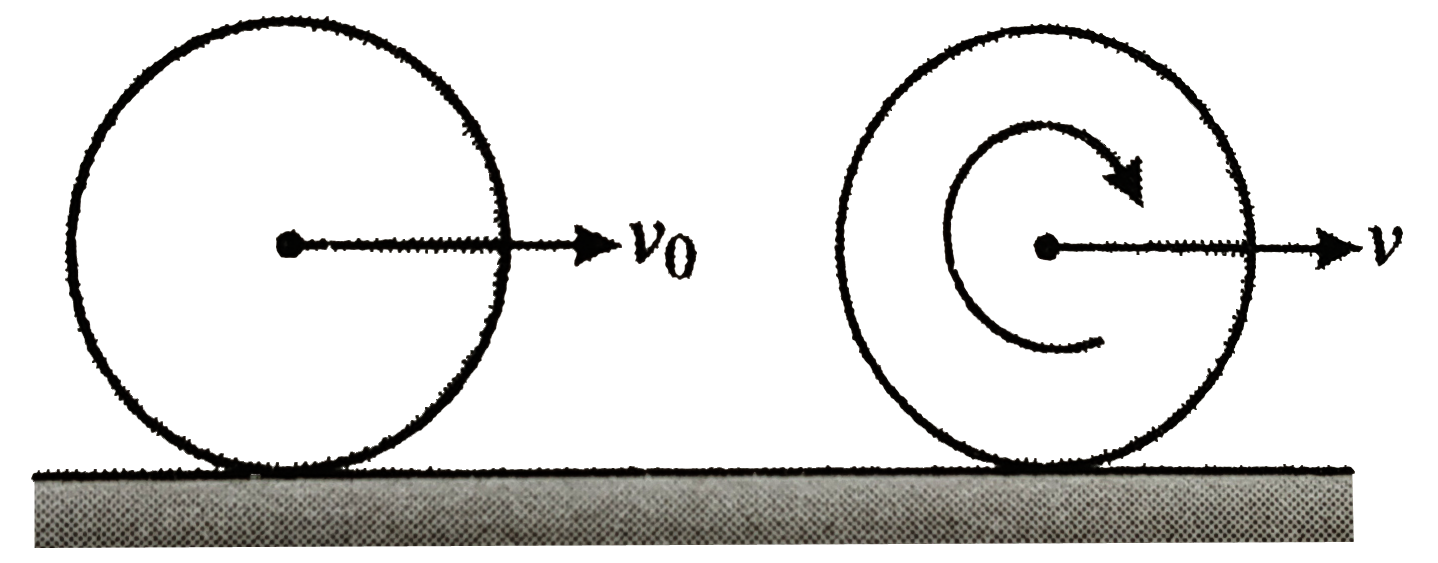
b. Assuming coefficient of friction to be μ calculate t0.
The work done by the frictional force as a function of time.
Total work done by the friction over a time t much longer than t0.
The velocity of the centre of mass of the disc at t=t0 is ………………………
Assuming coefficient of friction to be μ calculate t0…………….
Findi the expression for work done by the functional force as a function of time………………
What is the total work done by the friction over a time t much longer time t0 ?........................
(i) 23v0, (ii) v03μg, (iii) 12m(v0−μgt2)+12mr22(2μgtr)2−12mv20,(iv) −mv20/6
FBD of the disc is as shown.
When the disc is projected it starts sliding and hence there is a relative motion between the points of contact. Therefore, frictional force acts on the disc in the direction opposite to the motion.
 (i) Now for translational motion.
(i) Now for translational motion.
→aCM=→fm
f=μN (as it slides) =μg⇒acm=−μg, negative sign indicates that acm is opposite to vcm⇒vcm(t)=v0−μgt⇒t0=v0−vμg, when vcm(t0)=v ..........(i)
For rotational motion about centre
τCM=ICMα⇒μmgr=mr22αα=2μgr
ω(t)=0+2μgrt⇒ω(t0)2μgrv0−vμg=2(v0−v)r
vcm=ωr⇒v=2(v0−v)⇒v=23v0
(ii) Putting the value of v in Eq. (i) , we get t0=v03μg
(iii) Work done by the frictional force equal to change in K.E.
Wfriction=12m(v0−μgt)2+12mr2r−12mv20
(iv) Work done till time t0=12m(2v02)2+12mr22((2v0)23r)2−12mv20
=12mv20(49+29−1)=mv206
For time, t>t0, work done by the friction is zero as friction stops acting. Therefore, for longer total work done is W=−mv20/6.
Topper's Solved these Questions
- ROTATIONAL MOTION BOOK - VMC MODULES ENGLISHCHAPTER - ROTATIONAL MOTION EXERCISE - JEE Advanced (Archive) (True/False Type)
3 Videos
- ROTATIONAL MOTION BOOK - VMC MODULES ENGLISHCHAPTER - ROTATIONAL MOTION EXERCISE - JEE Advanced (Archive) (NUMERICAL VALUE TYPE)
15 Videos
- REVISION TEST-2 JEEBOOK - VMC MODULES ENGLISHCHAPTER - REVISION TEST-2 JEEEXERCISE - PHYSICS
25 Videos
- SIMPLE HARMONIC MOTION BOOK - VMC MODULES ENGLISHCHAPTER - SIMPLE HARMONIC MOTION EXERCISE - 7-previous year question
46 Videos
Similar Questions
A triangular platge of uniform thickness and densilty ismade to rotate about an axis perpendicular to the plane of the paper an a. passing through A b. passing through B, by the application of some foce F at C (mid point of AB) as show in figure. In which case is angular acceleration more?

View SolutionA small sphere rolls down without slipping from the top of a track in a vertical plane. The track has an elevated section and a horizontal part. The horizontall part is 1.0 meter above the ground level and the top of the track is 2.4 meter above the ground. Find the distance on the ground with respect to a point B( which is vetically below the end A of the track as shown in fig.) where the sphere lands.
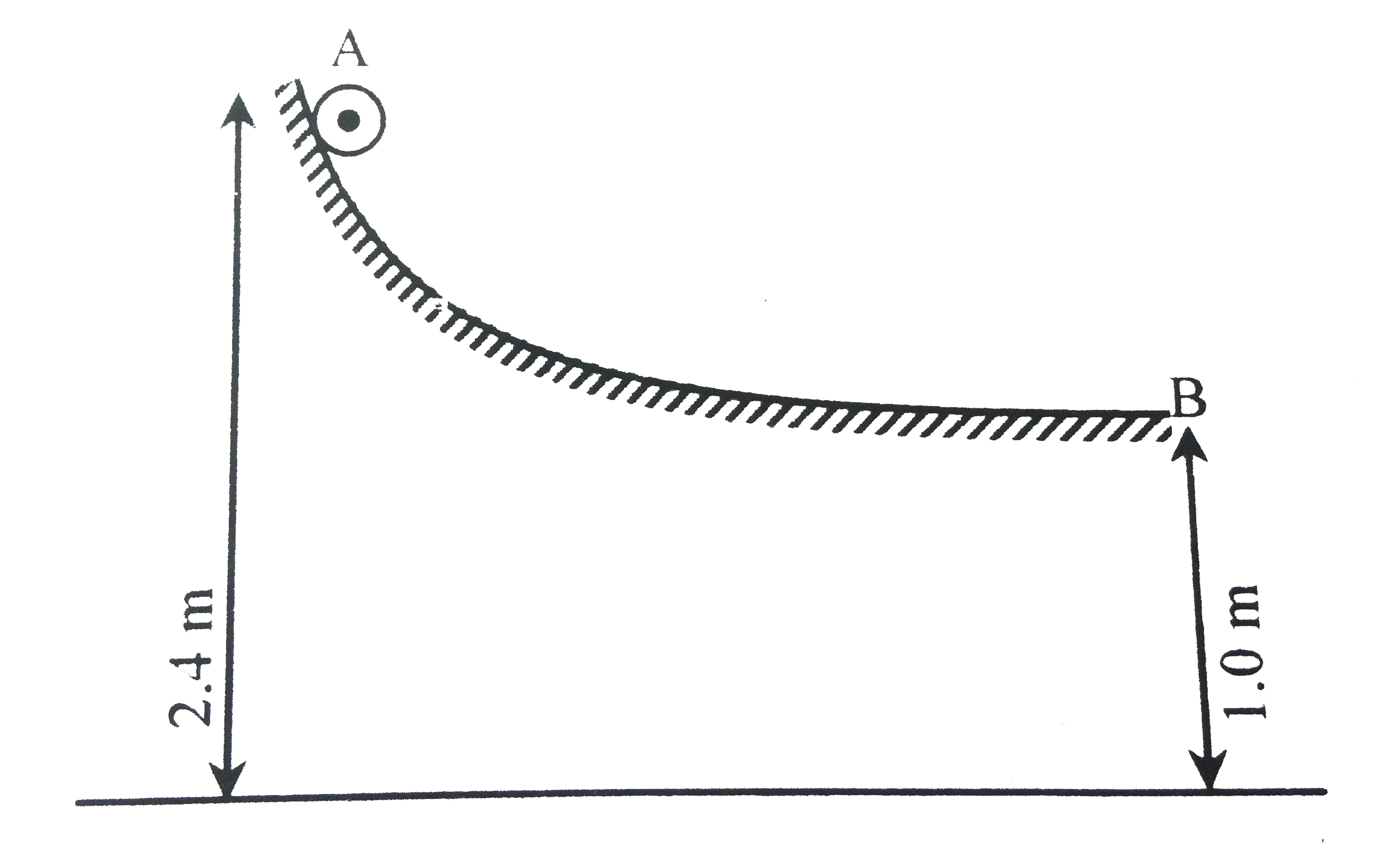 .
.
(A) 1m
(B) 2m
( C) 3m
(D) 4m.
View SolutionThree charges +Q, q, +Q are placed respectively, at distance, 0, d//2 and d from the origin, on the x-axis. If the net force experienced by +Q placed at x=0, is zero, then value of q is :
View SolutionTwo bodies M and N of equal masses are suspended from two separate massless springs of spring constants k1 and k2 respectively . If the two bodies oscillate vertically such that their maximum velocities are equal, the ratio of the amplitude of vibration of M to that on N is
View SolutionA uniform ring of radius R is given a back spin of angular velocity V_(0)//2R and thrown on a horizontal rough surface with velocity of centre to be V_(0) . The velocity of the centre of the ring when it starts pure rolling will be
View SolutionA uniform disk of mass m and radius R is projected horizontally with velocity v0 on a rough horizontal floor so that it starts off with a purely sliding motion at t=0. After t0 seconds it acquires a purely rolling motion as shown in figure.
(i) Calculate the velocity of the centre of mass of the disk at t0.

(ii) Assuming the coefficient of friction to be μ calculate t0. Also calculate the work done by the frictional force as a function of time and the total work done by it over a time t much longer than t0.
View SolutionA uniform disc of mass m and radius R is projected horizontally with velocity v_(0) on a rough horizontal floor so that it starts off with a purely sliding motion at t=0 . After t_(0) seconds, it acquires pure rolling motion as shown in the figure. (a) Calculate the velocity of the center of mass of the disc at t_(0) . Assuming that the coefficent of friction to be mu , calculate t_(0) .
View SolutionA small body of mass m is at rest inside a narrow groove carved in a disc. Groove is a circle of radius R concentric to the disc. Mass of the disc is also m . The disc lies on a smooth horizontal floor. The small body is given a sharp impulse so that it acquires a tangential velocity Vo at time t = 0.

(a) The velocity of the centre of the disc becomes zero for the first time at time t0. Find t0
(b) Find speed of the small body at time t03
View SolutionA uniform disc of mass m and radius R is projected horizontally with velocity v0 on a rough horizontal floor so that it starts with a purely sliding motion at t= 0. After t0 seconds it acquires a purely rolling motion.
(a) Calculate the velocity of the centre of mass of the disc at t0
(b) Assuming the coefficient of friction to be μ, calculate to. Also calculate the work done by the frictional force as a function of time and the total work done by it over a time t muchlonger than t0.
View SolutionA ring of mass m and radius R is placed on a rough horizontal surface (co-efficient of friction μ) with velocity of C.M.v0 and angular speed 2V0R as shown in figure. Initially the ring is rolling with slipping but attains pure rolling motion after some time t. Then
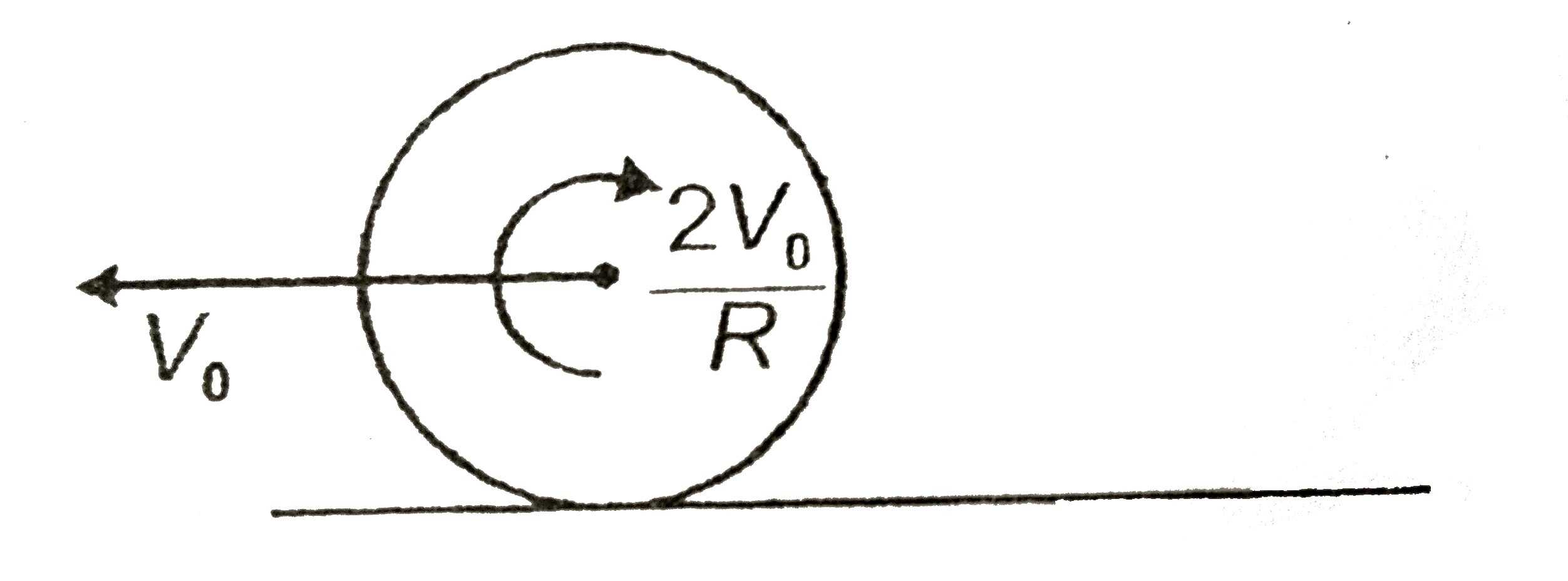
View SolutionA uniform disc having mass m and radius R v_(0) A rod is projected on a horizontal floor with velocity t in the horizontal direction it starts sliding at time t=0 t_(0) only slips for a second while t_(0) After a second it starts rolling as shown in the picture. a. Time t_(0) Calculate the center of mass velocity of the disc. b. If the value of coefficient of friction mu yes then t_(0) What will be the value of The work done by the frictional force (in terms of time) and the time t (which is t_(0) Also calculate the total work for
View SolutionA uniform ring of mass 'm' and radius 'R' is projected horizontally with velcoty v_(0) on a rough horizontal floor, so that it starts off with a purely sliding motion and it acquires a pure rolling motion after moving a distance d. If the coefficient of friction between the ground and ring is mu , then work done by the friction in the process is
View SolutionA sphere of mass m and radius R is kept on a rough floor. A sharp impulse is applied in the horizontal direction at the height of centre of sphere so that sphere acquires a linear velocity v0 without any angular velocity. Calculate the velocity of sphere when pure rolling starts.
View SolutionA cylinder is rotating with angular velocity omega_(0) and is gently put on a rough horizontal floor. Assume mass of the cylinder is m and radius R. Calculate the velocity of cylinder when it starts pure rolling on the surface.
View SolutionA solid sphere of radius R is projected on a rough horizontal surface of coefficient of friction with linear Speed v_(0) , at time to 0. It slips for some time, finally starts to roll with out slipping at time t =t_(0) .Find a) The linear velocity of its centre when pure rolling begins. b) The time t_(0)
View SolutionA solid sphere of radius R is projected on a rough horizontal surface of coefficient of friction with linear Speed v0, at time to 0. It slips for some time, finally starts to roll with out slipping at time t=t0 .Find a) The linear velocity of its centre when pure rolling begins. b) The time t0
View Solution
