The electric field at the centroid of an equilateral triangle carrying an equal charge q at each of the vertices is :
Zero
√2kgx2
kq√2x2
3kqx2
The correct Answer is:A
To find the electric field at the centroid of an equilateral triangle with equal charges q at each vertex, we can follow these steps:
Step 1: Understand the Configuration
We have an equilateral triangle with vertices A, B, and C, each carrying a charge q. The centroid (point C) is the point where the three medians of the triangle intersect.
Step 2: Determine the Electric Field Contribution from Each Charge
The electric field →E due to a point charge q at a distance r is given by:
→E=k⋅qr2^r
where k is Coulomb's constant, and ^r is the unit vector pointing away from the charge.
Step 3: Calculate the Magnitude of Electric Fields
Let R be the distance from each vertex to the centroid. The electric field due to each charge at the centroid will have the same magnitude:
E1=E2=E3=k⋅qR2
Step 4: Analyze the Direction of Electric Fields
- The electric field due to charge q at vertex A will point away from A towards the centroid.
- The electric field due to charge q at vertex B will point away from B towards the centroid.
- The electric field due to charge q at vertex C will point away from C towards the centroid.
Step 5: Resolve the Electric Fields into Components
Since the triangle is equilateral, the angles between the electric field vectors will be 120∘. We can resolve these vectors into horizontal and vertical components.
- The horizontal components of E1 and E2 will cancel each other out since they are equal in magnitude and opposite in direction.
- The vertical components will add up.
Step 6: Calculate the Resultant Electric Field
Let’s denote the angle between the electric field vector and the vertical as 30∘ (since the angles in an equilateral triangle are 60∘).
The vertical component of each electric field is:
Evertical=Esin(30∘)=E⋅12
Since there are two vertical components contributing to the total vertical electric field:
Enet vertical=2⋅E⋅12=E
Step 7: Conclusion
However, since the horizontal components cancel each other out, the net electric field at the centroid is:
→Enet=0
Thus, the electric field at the centroid of the triangle is zero.
Final Answer
The electric field at the centroid of an equilateral triangle carrying an equal charge q at each of the vertices is:
→E=0N/C
We have an equilateral triangle with vertices A, B, and C, each carrying a charge q. The centroid (point C) is the point where the three medians of the triangle intersect.
The electric field →E due to a point charge q at a distance r is given by:
→E=k⋅qr2^r
where k is Coulomb's constant, and ^r is the unit vector pointing away from the charge.
Let R be the distance from each vertex to the centroid. The electric field due to each charge at the centroid will have the same magnitude:
E1=E2=E3=k⋅qR2
- The electric field due to charge q at vertex A will point away from A towards the centroid.
- The electric field due to charge q at vertex B will point away from B towards the centroid.
- The electric field due to charge q at vertex C will point away from C towards the centroid.
Since the triangle is equilateral, the angles between the electric field vectors will be 120∘. We can resolve these vectors into horizontal and vertical components.
- The vertical components will add up.
Let’s denote the angle between the electric field vector and the vertical as 30∘ (since the angles in an equilateral triangle are 60∘).
Evertical=Esin(30∘)=E⋅12
Enet vertical=2⋅E⋅12=E
However, since the horizontal components cancel each other out, the net electric field at the centroid is:
→Enet=0
The electric field at the centroid of an equilateral triangle carrying an equal charge q at each of the vertices is:
→E=0N/C
Topper's Solved these Questions
- ELECTROSTATICSBook:VMC MODULES ENGLISHChapter:ELECTROSTATICSExercise:LEVEL - 2
Explore 60 Videos
- ELECTROSTATICSBook:VMC MODULES ENGLISHChapter:ELECTROSTATICSExercise:JEE MAIN
Explore 65 Videos
- ELECTROSTATICSBook:VMC MODULES ENGLISHChapter:ELECTROSTATICSExercise:LEVEL - 0 (LONG ANSWER TYPE )
Explore 8 Videos
- ELECTROMAGNETIC INDUCTION & ALTERNATIVE CURRENT Book:VMC MODULES ENGLISHChapter:ELECTROMAGNETIC INDUCTION & ALTERNATIVE CURRENT Exercise:IMPECCABLE
Explore 52 Videos
- ENERGY & MOMENTUMBook:VMC MODULES ENGLISHChapter:ENERGY & MOMENTUMExercise:JEE ADVANCE (ARCHIVE) - TRUE/FALSE TYPE
Explore 1 Video
Similar Questions
The magnetic induction field at the centroid or an equilateral triangle of side 'I' and carrying a current 'i' is
View SolutionA point charge +Q is placed at the centroid of an equilateral triangle. When a second charge +Q is placed at a vertex of the triangle, the magnitude of the electrostatic force on the central charge is 8 N. The magnitude of the net force on the central charge when a third charge +Q is placed at another vertex of the triangle is
View SolutionThree paricles, each of mass m and carrying a charge q each, are suspended from a common pointby insulating massless strings each of length L. If the particles are in equilibrium and are located at the corners of an equilateral triangle of side a, calculate the charge q on each particle. Assume L>>a.
View SolutionABC is an equilateral triangle. Charges +q are placed at each corner. The electric intensity at O will be
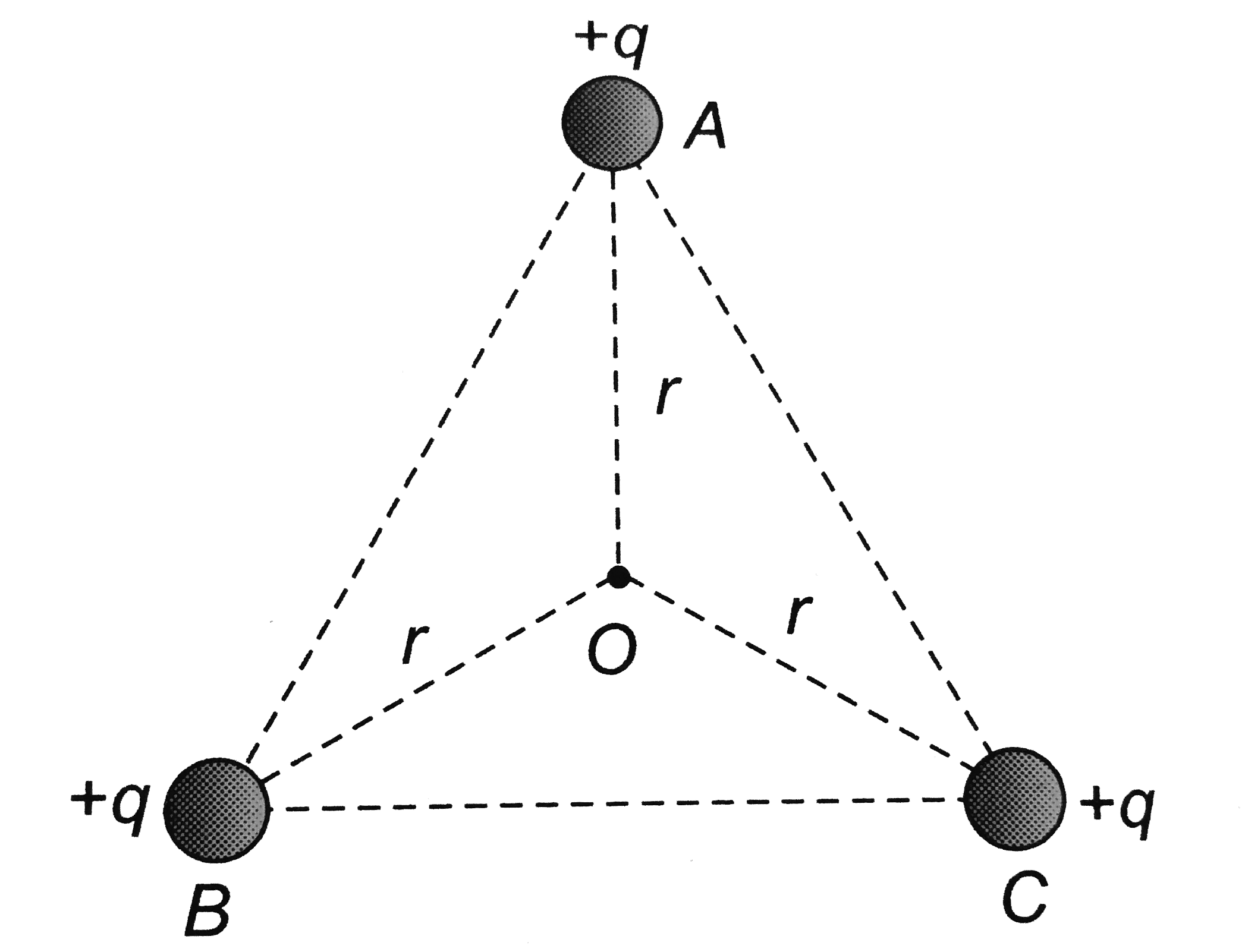
View SolutionABC is an equilateral triangle. Charges −2q are placed at each corner. The electric intensity at O will be

View SolutionThree equal masses of 2kg each are placed at the vertices of an equilateral triangle and a mass of 4 kg is placed at the centroid of the triangle which is at a distance of √2 m from each of the vertices of the triangle. The force, (in newton) acting on the mass of 4 kg is
View SolutionThree equal masses of 1.5 kg each are fixed at the vertices of an equilateral triangle of side 1 m. What is the force acting on a particle of mass 1 kg placed at its centroid ?
View SolutionThree equal charge q0 each are placed at three corners of an equilateral triangle of side 'a'. Find out force acting on one of the charge due to other two charges ?
View SolutionThree equal charges, each +q are placed on the corners of an equilatreal triangel . The electric field intensity at the centroid of the triangle is
View SolutionIf 3 charges are placed at the vertices of equilateral triangle of charge 'q' each. What is the net potential energy, if the side of equilateral Δ is lcm ?
View Solution
