A hall has the dimensions 10m × 10m × 10 m. A fly starting at one corner ends up at a diagonally opposite corner. The magnitude of its displacement is nearly
5√2m
10√3m
20√3m
30√3m
The correct Answer is:B
To find the magnitude of the displacement of the fly that starts at one corner of a cube and ends up at the diagonally opposite corner, we can follow these steps:
1. Understand the Problem:
- We have a cube (hall) with dimensions 10m x 10m x 10m.
- The fly starts at one corner (let's call it point A) and ends at the diagonally opposite corner (point B).
2. Identify the Coordinates:
- Let's assign coordinates to the corners of the cube:
- Point A (0, 0, 0) - starting corner
- Point B (10, 10, 10) - diagonally opposite corner
3. Use the Displacement Formula:
- The displacement vector can be calculated using the distance formula in three-dimensional space:
Displacement=√(x2−x1)2+(y2−y1)2+(z2−z1)2
- Here, (x1,y1,z1) are the coordinates of point A and (x2,y2,z2) are the coordinates of point B.
4. Substitute the Coordinates:
- Substitute the coordinates of points A and B into the formula:
Displacement=√(10−0)2+(10−0)2+(10−0)2
5. Calculate Each Term:
- Calculate the squares:
=√102+102+102=√100+100+100=√300
6. Simplify the Expression:
- The square root of 300 can be simplified:
√300=√100×3=10√3
7. Final Result:
- Therefore, the magnitude of the displacement of the fly is:
Displacement≈10√3 meters
- We have a cube (hall) with dimensions 10m x 10m x 10m.
- The fly starts at one corner (let's call it point A) and ends at the diagonally opposite corner (point B).
- Let's assign coordinates to the corners of the cube:
- Point A (0, 0, 0) - starting corner
- Point B (10, 10, 10) - diagonally opposite corner
- The displacement vector can be calculated using the distance formula in three-dimensional space:
Displacement=√(x2−x1)2+(y2−y1)2+(z2−z1)2
- Here, (x1,y1,z1) are the coordinates of point A and (x2,y2,z2) are the coordinates of point B.
- Substitute the coordinates of points A and B into the formula:
Displacement=√(10−0)2+(10−0)2+(10−0)2
- Calculate the squares:
=√102+102+102=√100+100+100=√300
- The square root of 300 can be simplified:
√300=√100×3=10√3
- Therefore, the magnitude of the displacement of the fly is:
Displacement≈10√3 meters
Topper's Solved these Questions
- MOTION IN A STRAIGHT LINE & PLANE BOOK - VMC MODULES ENGLISHCHAPTER - MOTION IN A STRAIGHT LINE & PLANE EXERCISE - IMPECCABLE
52 Videos
- MOTION IN A STRAIGHT LINE & PLANE BOOK - VMC MODULES ENGLISHCHAPTER - MOTION IN A STRAIGHT LINE & PLANE EXERCISE - ENABLE
50 Videos
- MOCK TEST 9BOOK - VMC MODULES ENGLISHCHAPTER - MOCK TEST 9EXERCISE - PHYSICS (SECTION 2)
5 Videos
- Motion in Straight Line BOOK - VMC MODULES ENGLISHCHAPTER - Motion in Straight Line EXERCISE - IN-CHAPTER EXERCISE-J
10 Videos
Similar Questions
A room has dimensions 3m×4m×5m. A fly starting at one corner ends up at the diamertrically opposite corner. The magnitude of the displacement of the fly is
View SolutionA room has dimensions 3 m xx 4 m xx5 m. A fly starting at one cronet ends up at the diametrically opposite corner. (a) What is the magnitude of its displacement ? (a) What is the magnitude of its displacement ? (b) If the fly wer to walk, what is the length of the shortest pothe it cantake ?
View SolutionA boy walks uniformly along the sides of a rectangular park of size 400m×300m, starting from one corner to the other corner diagonally opposite. Which of the following statements is incorrect?
View SolutionA cubical room has dimensions 4ft×4ft×4ft . An insect starts from one corner O and reaches a corner on the opposite side of the body diagonal.
In previous problem, the magnitude of displacement is :
View SolutionA cubical room has dimensions 4ft×4ft×4ft . An insect starts from one corner O and reaches a corner on the opposite side of the body diagonal.
Suppose that insect does not fly but crawls. Find the minimum distance travelled by insect to reach the destination.
View SolutionA car 2m long and 3m wide is moving at 10m/s when a bullet hits it in a direction making an angle of tan−1(3/4) with the car as seen from the ground. The bullet enters one edge of the car at the corner and passes out at diagonally opposite corner. Neglecting gravity, the time for the bullet to cross the car is
View SolutionA plot of land in the form of a rectangle has a dimension 240m×180m. A drain 10m wide is dug all around it (on the outside) and the earth dug out is evenly spread over the plot, increasing its surface level by 25cm. Find the depth of the drain let.
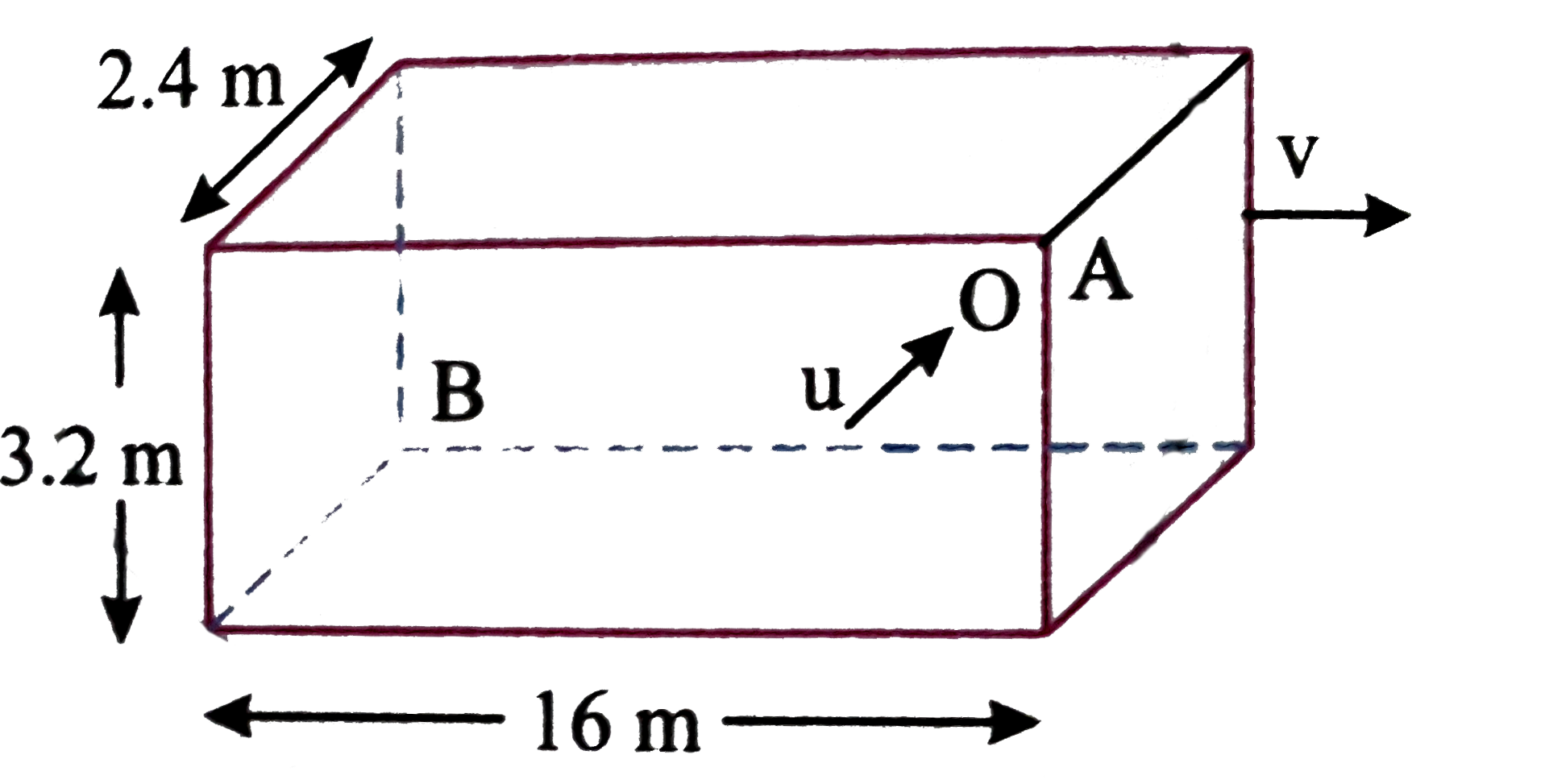
View SolutionA railway compartments is 16m long, 2.4m wide and 3.2m high. It is moving with a velocity v A particle moving horizontally with a speed u perpendicular to the direction of v enters through a hole at an upper corner A and strikes the diagonally opposite corner B.Assume g=10m/s2.
View SolutionA metallic rod of length 1m has one end free and other end rigidly clamped. Longitudinal stationary waves are set up in the rod in such a way that there are total six antinodes present along the rod. The amplitude of an antinode is 4×10−6m. young's modulus and density of the rod are 6.4×1010N/m2 and 4×103Kg/m3 respectively. Consider the free end to be at origin and at t=0 particles at free end are at positive extreme.
The magnitude of strain at midpoint of the rod at t=1sec is
View SolutionA field is 15m long and 12m broad. At one corner of this field a rectangular well of dimensions 8m×2.5m×2m is dug and the dug-out soil is spread evenly over the rest of the field. Find the rise in the level of the rest of the field.
View Solution
