An empty plastic box of mass 5 kg is observed to accelerate up at the rate of g/6 when placed deep inside water. What mass of sand should be put inside the box so that it may accelerate dow at the rate of g/6 ?
1 kg
1.5 kg
2 kg
2.5 kg
The correct Answer is:3
To solve the problem step by step, we will analyze the forces acting on the plastic box in both scenarios: when it accelerates upwards and when it accelerates downwards.
Step 1: Analyze the upward acceleration
1. Given Data:
- Mass of the empty plastic box, m=5kg
- Upward acceleration, a=g6
2. Forces Acting on the Box:
- Weight of the box, W=mg=5g (downward)
- Buoyant force, Fb (upward)
3. Using Newton's Second Law:
- The net force acting on the box can be expressed as:
Fnet=Fb−W
- According to Newton's second law, this net force is also equal to the mass times the acceleration:
Fnet=ma=5⋅g6=5g6
4. Setting the Equations Equal:
Fb−5g=5g6
Rearranging gives:
Fb=5g+5g6=30g6+5g6=35g6
Step 2: Analyze the downward acceleration
1. Now, we want the box to accelerate downward at the same rate:
- Downward acceleration, a=g6
- Let the mass of sand added to the box be M.
2. Forces Acting on the Box with Sand:
- Total weight of the box with sand, W′=(m+M)g=(5+M)g (downward)
- Buoyant force remains the same, Fb=35g6 (upward)
3. Using Newton's Second Law Again:
- The net force acting on the box with sand is:
Fnet=Fb−W′=35g6−(5+M)g
- According to Newton's second law:
Fnet=(5+M)⋅g6
4. Setting the Equations Equal:
35g6−(5+M)g=(5+M)⋅g6
Simplifying gives:
35g6−5g−Mg=(5+M)⋅g6
35g6−30g6−Mg=5g6+Mg6
5g6−Mg=5g6+Mg6
5. Rearranging the Equation:
−Mg−Mg6=0
−6Mg+Mg6=0
−7Mg6=0
This implies:
7M=10⇒M=107≈1.43kg
Final Step: Calculate the mass of sand needed
To achieve a downward acceleration of g6, the mass of sand that should be added to the box is approximately 2kg.
1. Given Data:
- Mass of the empty plastic box, m=5kg
- Upward acceleration, a=g6
- Weight of the box, W=mg=5g (downward)
- Buoyant force, Fb (upward)
- The net force acting on the box can be expressed as:
Fnet=Fb−W
- According to Newton's second law, this net force is also equal to the mass times the acceleration:
Fnet=ma=5⋅g6=5g6
Fb−5g=5g6
Rearranging gives:
Fb=5g+5g6=30g6+5g6=35g6
1. Now, we want the box to accelerate downward at the same rate:
- Downward acceleration, a=g6
- Let the mass of sand added to the box be M.
- Total weight of the box with sand, W′=(m+M)g=(5+M)g (downward)
- Buoyant force remains the same, Fb=35g6 (upward)
- The net force acting on the box with sand is:
Fnet=Fb−W′=35g6−(5+M)g
- According to Newton's second law:
Fnet=(5+M)⋅g6
35g6−(5+M)g=(5+M)⋅g6
Simplifying gives:
35g6−5g−Mg=(5+M)⋅g6
35g6−30g6−Mg=5g6+Mg6
5g6−Mg=5g6+Mg6
−Mg−Mg6=0
−6Mg+Mg6=0
−7Mg6=0
This implies:
7M=10⇒M=107≈1.43kg
To achieve a downward acceleration of g6, the mass of sand that should be added to the box is approximately 2kg.
Topper's Solved these Questions
- LAWS OF MOTION BOOK - VMC MODULES ENGLISHCHAPTER - LAWS OF MOTION EXERCISE - ENABLE
50 Videos
- LAWS OF MOTION BOOK - VMC MODULES ENGLISHCHAPTER - LAWS OF MOTION EXERCISE - EFFICIENT
50 Videos
- KINEMATICS OF A PARTICLE BOOK - VMC MODULES ENGLISHCHAPTER - KINEMATICS OF A PARTICLE EXERCISE - JEE Advanced (archive)
14 Videos
- LIQUIDSBOOK - VMC MODULES ENGLISHCHAPTER - LIQUIDSEXERCISE - JEE ADVANCED (LEVEL -2)
55 Videos
Similar Questions
A jet is releasing water at the rate of 6 kg/see with speed of 4 m/sec. Now this water strikes a block of mass 10 kg. find the force exerted on block & its acceleration ?
View SolutionA hot- air balloon consists of a basket, one passenger, and some carge. Let the total mass be M. Even though there is an upward lift force on the balloon, the balloon is initially acceleration downwards at a rate of g/3.
(a) Draw a free-body diagram for the descending balloon.
(b) Find the upward lift force in terms of the initial total weight Mg.
(c ) The passenger notices that he is heading straight for a waterfall and decides he needs to go up. What fraction of the total weight must he drop overboard so that the balloon accelerates upward at a rate of g/2? Assume that the upward lift force remains the same.
View SolutionA box is put on a scale which is adjusted to read zero, when the box is empty. A stream of pebbles is then poured into the base from a height h above its bottom at a rate of n pebbles/s. Each pebble has a mass m. If the pebbles collide with the box such that they immediately come to rest after collision, then the scale reading at time t after the pebbles begin to fill the box is [ neglect piling up of pebbles]
View SolutionA paritcal of mass 10g moves along a circle of radius 6.4cm with a constant tangennitial acceleration. What is the magnitude of this acceleration . What is the magnitude of this acceleration if the kinetic energy of the partical becomes equal to 8×10−4J by the end of the second revolution after the beginning of the motion?
View SolutionWith what acceleration a should the box of figure descends so that the block of mass M exerts a force Mg/4 on the floor of the box?
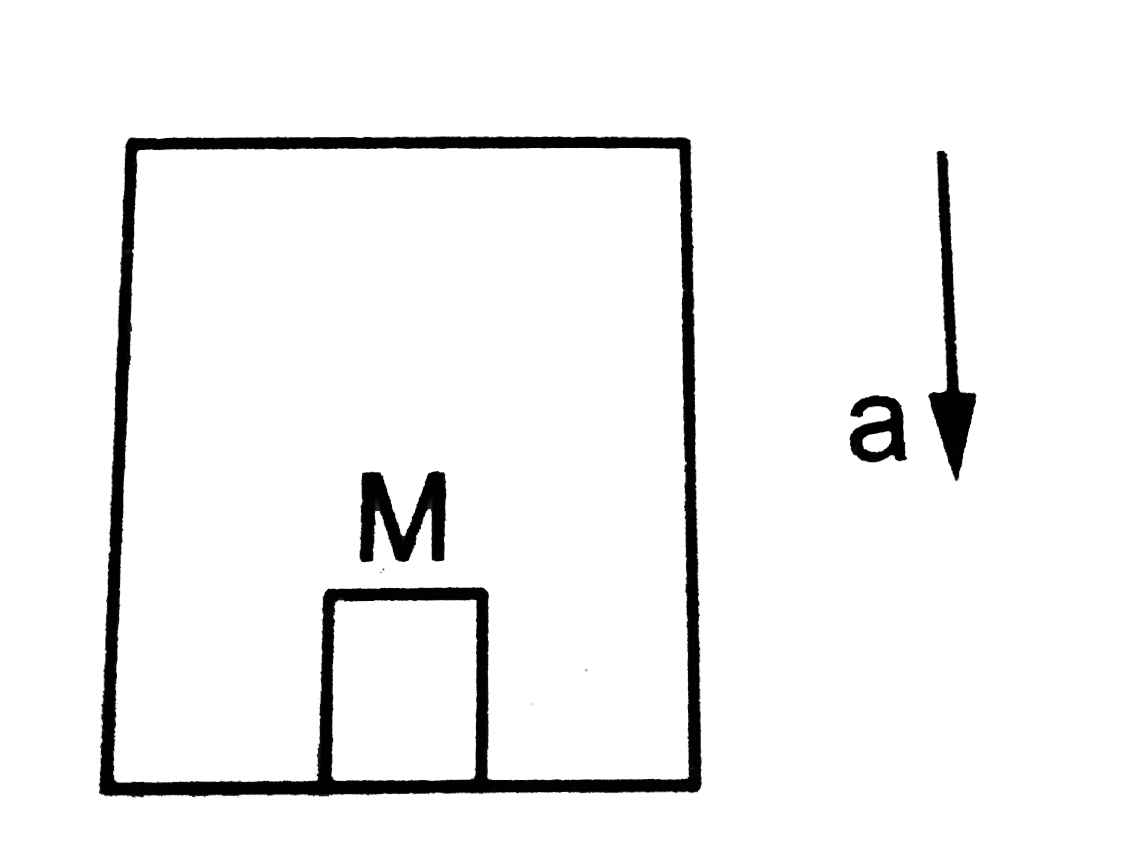
View SolutionTwo blocks of mass 5 kg and 3 kg are attached to the ends of a string passing over a smooth pulley fixed to the ceiling of an elevator. A man inside the elevator accelerated upwards, finds the acceleration of the blocks to be 932g. The acceleration of the elevator is
View SolutionOn the horizontal surface of a truck (μ=0.6) a block of mass 1 kg is placed. If the truck is accelerating at the rate of 5m/sec2 then friction force on the block will be
View SolutionThe time period of a simple pendulum inside a stationary lift is √5 s. What will be the time period when the lift moves upward with an acceleration g4?
View SolutionA monkey of mass 20kg is holding a vertical rope. The rope will not break when a mass of 25kg is suspended from it but will break it the mass exeeds 25kg . What is the maximum acceleration with which the monkey can climb up along the rope? (g=10m/s2) .
View SolutionA monkey of mass 20kg is holding a vertical rope. The rope will not break when a mass of 25kg is suspended from it but will break it the mass exeeds 25kg . What is the maximum acceleration with which the monkey can climb up along the rope? (g=10m/s2) .
View Solution
