Two blocks of mass 5 kg and 3 kg are attached to the ends of a string passing over a smooth pulley fixed to the ceiling of an elevator. A man inside the elevator accelerated upwards, finds the acceleration of the blocks to be . The acceleration of the elevator is
The correct Answer is:C
To solve the problem, we need to analyze the forces acting on the two blocks and relate them to the acceleration of the elevator. Let's break it down step by step.
Step 1: Understand the System
We have two blocks:
- Block 1 (mass m1=5kg)
- Block 2 (mass m2=3kg)
These blocks are connected by a string over a pulley. The elevator is accelerating upwards, and a man inside the elevator measures the acceleration of the blocks to be 932g.
Step 2: Identify Forces Acting on Each Block
For Block 1 (5 kg):
- Weight W1=m1g=5g
- Tension in the string T
For Block 2 (3 kg):
- Weight W2=m2g=3g
- Tension in the string T
Step 3: Write the Equations of Motion
Since the elevator is accelerating upwards, we need to consider the effective acceleration due to gravity. The effective gravitational force acting on each block is modified by the acceleration of the elevator ae.
For Block 1 (5 kg):
T−5g−5ae=−5a
(Here, a is the acceleration of the block relative to the elevator.)
For Block 2 (3 kg):
3g+3ae−T=3a
Step 4: Substitute Known Values
We know that the acceleration of the blocks as observed by the man in the elevator is a=932g.
Step 5: Solve the Equations
Now we can add the two equations to eliminate T:
1. From Block 1:
T=5g+5ae−5a
2. From Block 2:
T=3g+3ae+3a
Setting them equal to each other:
5g+5ae−5a=3g+3ae+3a
Step 6: Rearranging the Equation
Rearranging gives:
5g−3g+5ae−3ae=5a+3a
2g+2ae=8a
ae=4a−g
Step 7: Substitute the Value of a
Substituting a=932g:
ae=4(932g)−g
ae=3632g−3232g
ae=432g=18g
Final Answer
The acceleration of the elevator is:
18g
We have two blocks:
- Block 1 (mass m1=5kg)
- Block 2 (mass m2=3kg)
For Block 1 (5 kg):
- Weight W1=m1g=5g
- Tension in the string T
- Weight W2=m2g=3g
- Tension in the string T
Since the elevator is accelerating upwards, we need to consider the effective acceleration due to gravity. The effective gravitational force acting on each block is modified by the acceleration of the elevator ae.
T−5g−5ae=−5a
(Here, a is the acceleration of the block relative to the elevator.)
3g+3ae−T=3a
We know that the acceleration of the blocks as observed by the man in the elevator is a=932g.
Now we can add the two equations to eliminate T:
T=5g+5ae−5a
T=3g+3ae+3a
5g+5ae−5a=3g+3ae+3a
Rearranging gives:
5g−3g+5ae−3ae=5a+3a
2g+2ae=8a
ae=4a−g
Substituting a=932g:
ae=4(932g)−g
ae=3632g−3232g
ae=432g=18g
The acceleration of the elevator is:
18g
Topper's Solved these Questions
- LAWS OF MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - LAWS OF MOTIONEXERCISE - Match the columns
7 Videos
- LAWS OF MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - LAWS OF MOTIONEXERCISE - Medical entrances gallery
39 Videos
- LAWS OF MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - LAWS OF MOTIONEXERCISE - Check point 5.4
20 Videos
- KINEMATICS 1BOOK - DC PANDEY ENGLISHCHAPTER - KINEMATICS 1EXERCISE - INTEGER_TYPE
15 Videos
- LAWS OF THERMODYNAMICSBOOK - DC PANDEY ENGLISHCHAPTER - LAWS OF THERMODYNAMICSEXERCISE - Level 2 Subjective
18 Videos
Similar Questions
Two blocks of masses 6kg and 4kg are attached to the two ends of a massless string passing over a smooth fixed pulley. if the system is released, the acceleration of the centre of mass of the system will be
View SolutionA spring of force constant 200Nm−1 has a block of mass 10 kg hanging at its one end and the other end of the spring is attached to the celling of an elevator. The elevator is rising upwards with an acceleration of g4 and the block is in equilibrium with respect to the elevator . when the acceleration of the elevator suddenly ceases , the block starts oscillating . What is the amplitude (in m) of these oscillations ?
View Solution
Knowledge Check
Two blocks of masses of 40 kg and 30 kg are connected by a weightless string passing over a frictionless pulley as shown in the figure.
 A0.7ms−2B0.8ms−2C0.6ms−2D0.5ms−2
A0.7ms−2B0.8ms−2C0.6ms−2D0.5ms−2
Two bodies of masses 4 kg and 6 kg are tied to the ends of a massless string. The string passes over a frictionless pulley. The acceleration of the system is :
View SolutionTwo bodies of mass 4kg and 6kg are attached to the ends of a string passing over a pulley. The 4kg mass is attached to the table top by another string. The tension in this string T1 is equal to: Take
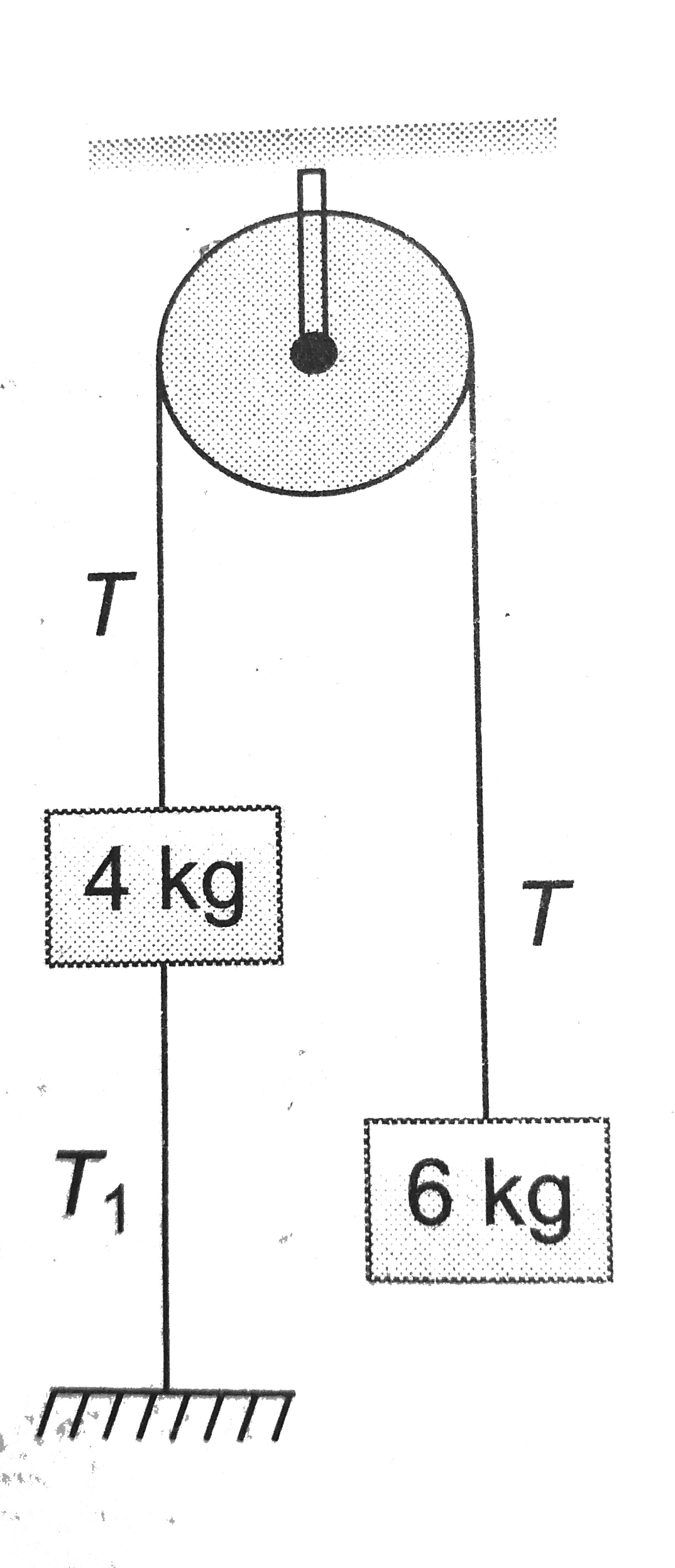
View SolutionTwo blocks of masses 2 kg and 4 kg are connected by a light string passing over a light smooth pulley clamped to the edge of a horizontal table. The 2 kg block is on the smooth horizontal table and the other block is hanging vertically, (i) Find the acceleration of the stem if it is released from rest, (ii) Find the tension in the string.
View SolutionA pulley is attached to the celing of a lift moing upwards. Two particles are attached to the two ends of a stirng passing over the pulley. The masses of the particles are in the ration 2:1 if the acceleration of the particles is g/2, then the acceleration of the lift will be
View SolutionA block of mass 1kg hangs without vibrations at the end of a spring with a force constant 1N/m attached to the ceilling of an elevator. The elevator is rising with an upward acceleration of g/4. The acceleration of the elevator suddenly ceases. What is the amplitude of the resulting oscillations?
View SolutionTwo blocks of masses 2 kg and 4 kg tied to a string passing over a frictionless pulley. What will be the magnitude of acceleration of the masses, when they are allowed to move freely?
View SolutionTwo unequal masses of 1kg and 2kg are connected by an inextensible light string passing over a smooth pulley as shown in figure. A force F=20N is applied on 1kg block find the acceleration of either block (g=10m/s2).

View Solution
