As body of mass 5 kg is suspended by the stirngs making angles 60∘ and 30∘ with the horizontal :
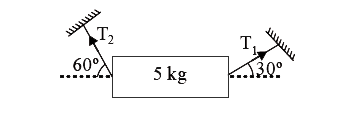
As body of mass 5 kg is suspended by the stirngs making angles 60^(@) and 30^(@) with the horizontal : (a) T(1) = 25N (b) T(2) = 25 N ( c ) T(1) = 25 sqrt( 3) N ( d ) T(2) = 25 sqrt( 3) N
(a) T1=25N (b) T2=25N
( c ) T1=25√3N ( d ) T2=25√3N

A

(A)a,b,

B

(B)a,d

C

(C)c,d

D

(D)b,c

Video Solution
Doubtnut Promotions Banner
Text Solution
Verified by Experts

The correct Answer is:2

Updated on:21/07/2023
|
Answer

Step by step video & image solution for As body of mass 5 kg is suspended by the stirngs making angles 60^(@) and 30^(@) with the horizontal : (a) T_(1) = 25N (b) T_(2) = 25 N ( c ) T_(1) = 25 sqrt( 3) N ( d ) T_(2) = 25 sqrt( 3) N by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.

Updated on:21/07/2023