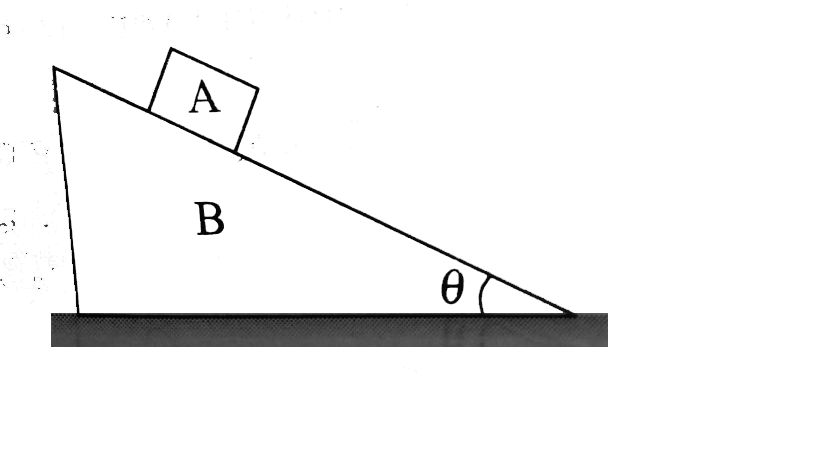
Body A is placed on frictionless wedge making an angle θ with the horizon. The horizontal acceleration towards left to be imparted to the wedge for the body A to freely fall vertically, is-
(a)gsinθ
(b)gcosθ
(c)gtanθ
(d)gcotθ
The correct Answer is:D
To solve the problem of finding the horizontal acceleration that needs to be imparted to the wedge so that body A falls vertically, we can follow these steps:
1. Understanding the Setup:
- We have a wedge inclined at an angle θ with the horizontal.
- A body A is placed on this frictionless wedge.
- We need to find the horizontal acceleration a of the wedge towards the left such that body A falls vertically.
2. Forces Acting on Body A:
- The weight of body A acting downwards is mg, where m is the mass of body A and g is the acceleration due to gravity.
- The normal force N exerted by the wedge on body A acts perpendicular to the surface of the wedge.
3. Components of Forces:
- The normal force can be resolved into two components:
- Horizontal component: Nsinθ
- Vertical component: Ncosθ
4. Condition for Vertical Fall:
- For body A to fall vertically, the horizontal acceleration of the wedge a must equal the horizontal component of the force acting on body A due to the normal force.
- Therefore, we can write the equation:
Nsinθ=ma
5. Vertical Forces on Body A:
- The vertical forces acting on body A must also balance out. The weight mg must equal the vertical component of the normal force:
mg=Ncosθ
6. Solving for Normal Force:
- From the second equation, we can express N:
N=mgcosθ
7. Substituting Normal Force:
- Substitute the expression for N into the first equation:
mgcosθsinθ=ma
8. Simplifying the Equation:
- This simplifies to:
mgsinθcosθ=ma
9. Canceling Mass:
- Cancel m from both sides (assuming m≠0):
gsinθcosθ=a
10. Final Expression:
- Therefore, the required horizontal acceleration a of the wedge is:
a=gtanθ
Final Answer:
The horizontal acceleration towards the left that needs to be imparted to the wedge for body A to fall vertically is a=gtanθ.
- We have a wedge inclined at an angle θ with the horizontal.
- A body A is placed on this frictionless wedge.
- We need to find the horizontal acceleration a of the wedge towards the left such that body A falls vertically.
- The weight of body A acting downwards is mg, where m is the mass of body A and g is the acceleration due to gravity.
- The normal force N exerted by the wedge on body A acts perpendicular to the surface of the wedge.
- The normal force can be resolved into two components:
- Horizontal component: Nsinθ
- Vertical component: Ncosθ
- For body A to fall vertically, the horizontal acceleration of the wedge a must equal the horizontal component of the force acting on body A due to the normal force.
- Therefore, we can write the equation:
Nsinθ=ma
- The vertical forces acting on body A must also balance out. The weight mg must equal the vertical component of the normal force:
mg=Ncosθ
- From the second equation, we can express N:
N=mgcosθ
- Substitute the expression for N into the first equation:
mgcosθsinθ=ma
- This simplifies to:
mgsinθcosθ=ma
- Cancel m from both sides (assuming m≠0):
gsinθcosθ=a
- Therefore, the required horizontal acceleration a of the wedge is:
a=gtanθ
The horizontal acceleration towards the left that needs to be imparted to the wedge for body A to fall vertically is a=gtanθ.
Topper's Solved these Questions
- LAWS OF MOTION BOOK - VMC MODULES ENGLISHCHAPTER - LAWS OF MOTION EXERCISE - EFFICIENT
50 Videos
- LAWS OF MOTION BOOK - VMC MODULES ENGLISHCHAPTER - LAWS OF MOTION EXERCISE - IMPECCABLE
53 Videos
- LAWS OF MOTION BOOK - VMC MODULES ENGLISHCHAPTER - LAWS OF MOTION EXERCISE - IMPECCABLE
53 Videos
- KINEMATICS OF A PARTICLE BOOK - VMC MODULES ENGLISHCHAPTER - KINEMATICS OF A PARTICLE EXERCISE - JEE Advanced (archive)
14 Videos
- LIQUIDSBOOK - VMC MODULES ENGLISHCHAPTER - LIQUIDSEXERCISE - JEE ADVANCED (LEVEL -2)
55 Videos
Similar Questions
A block is placed on a smooth wedge of inclination angle θ with the horizontal. What minimum acceleration should be given to the wedge in the horizontal direction so that the block starts moving up along the incline?
View SolutionThe acceleration of system of two bodies over the wedge as shown in figure is

View Solution
Knowledge Check
If a body is projected with an angle θ to the horizontal, then
Aits velocity is always perpendicular to its acceleration thenBits velocity becomes zero at its maximum height.Cits velocity makes zero angle with the horizontal at its maximum height.Dthe body just before hitting the ground, the direction of velocity coincides with the acceleration.
A block is placed on a smooth inclined plane at an angle 'θ' to the horizontal. The acceleration must the plane be moved horizontally so that the block to fall freely is
View SolutionA block slides down a frictionless, inclined plane that makes a 30∘ angle with the horizontal. Find the acceleration of this block.
View SolutionA body of mass m is projected with intial speed u at an angle θ with the horizontal. The change in momentum of body after time t is :-
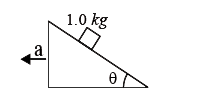
View SolutionA block of mass 1.0 kg rests on a wedge of angle θ. The acceleration which should be given to the wedge so that the block falls freely is :
View SolutionAll surfaces are smooth in following figure. Find F, such that block remain stationary with respect to wedge.

View SolutionA body is projected from ground with velocity u making an angle θ with horizontal. Horizontal range of body is four time to maximum height attained by body. Find out
(i) angle of projection
(ii) Range and maximum height in terms of u
(iii) ratio of kinetic energy to potential energy of body at maximum height
View SolutionA uniform stick of mass M is placed in a frictionless well as shown. The stick makes an angle θ with the horizontal. Then the force which the vertical wall exerts on right end of stick is :

View Solution
