A triangular block of mass M with angle 30º, 60º, 90º rests with its 30º– 90º side on a horizontal smooth fixed table. A cubical block of mass m rests on the 60º – 30º sideofthe triangular block. What horizontal acceleration a must M have relative to the stationary table so that m remains stationary with respect to the triangular block [M = 9 kg, m = 1 kg]
2.8m/s2
5.6m/s2
8.4m/s2
Zero
The correct Answer is:2
To solve the problem, we need to find the horizontal acceleration a that the triangular block of mass M must have so that the cubical block of mass m remains stationary with respect to the triangular block.
1. Understanding the Setup:
- We have a triangular block with angles 30º, 60º, and 90º. The 30º-90º side is on a smooth horizontal table.
- A cubical block of mass m rests on the 60º-30º side of the triangular block.
2. Identify Forces Acting on the Cubical Block:
- The weight of the cubical block m acts downward, which is mg (where g is the acceleration due to gravity).
- There is a pseudo force acting on the cubical block due to the acceleration a of the triangular block. This pseudo force acts horizontally to the left with magnitude ma.
3. Setting Up the Free Body Diagram (FBD):
- The cubical block experiences a gravitational force mg acting downwards.
- The pseudo force ma acts horizontally to the left.
- The block is in equilibrium with respect to the triangular block, meaning the forces must balance.
4. Resolving Forces:
- The gravitational force can be resolved into components along the incline of the triangular block:
- The component of the weight acting parallel to the incline (down the slope) is mgsin(30∘).
- The component of the pseudo force acting perpendicular to the incline is macos(30∘).
5. Balancing Forces:
- For the cubical block to remain stationary with respect to the triangular block, the forces must balance:
mgsin(30∘)=macos(30∘)
- Substituting sin(30∘)=12 and cos(30∘)=√32:
mg⋅12=ma⋅√32
6. Substituting Known Values:
- Given m=1kg and g≈9.8m/s2:
1⋅9.8⋅12=1⋅a⋅√32
- Simplifying gives:
4.9=a⋅√32
7. Solving for a:
- Rearranging the equation:
a=4.9⋅2√3=9.8√3≈5.66m/s2
Final Answer:
The required horizontal acceleration a that the triangular block must have is approximately 5.66m/s2.
- We have a triangular block with angles 30º, 60º, and 90º. The 30º-90º side is on a smooth horizontal table.
- A cubical block of mass m rests on the 60º-30º side of the triangular block.
- The weight of the cubical block m acts downward, which is mg (where g is the acceleration due to gravity).
- There is a pseudo force acting on the cubical block due to the acceleration a of the triangular block. This pseudo force acts horizontally to the left with magnitude ma.
- The cubical block experiences a gravitational force mg acting downwards.
- The pseudo force ma acts horizontally to the left.
- The block is in equilibrium with respect to the triangular block, meaning the forces must balance.
- The gravitational force can be resolved into components along the incline of the triangular block:
- The component of the weight acting parallel to the incline (down the slope) is mgsin(30∘).
- The component of the pseudo force acting perpendicular to the incline is macos(30∘).
- For the cubical block to remain stationary with respect to the triangular block, the forces must balance:
mgsin(30∘)=macos(30∘)
- Substituting sin(30∘)=12 and cos(30∘)=√32:
mg⋅12=ma⋅√32
- Given m=1kg and g≈9.8m/s2:
1⋅9.8⋅12=1⋅a⋅√32
- Simplifying gives:
4.9=a⋅√32
- Rearranging the equation:
a=4.9⋅2√3=9.8√3≈5.66m/s2
The required horizontal acceleration a that the triangular block must have is approximately 5.66m/s2.
Topper's Solved these Questions
- LAWS OF MOTION BOOK - VMC MODULES ENGLISHCHAPTER - LAWS OF MOTION EXERCISE - EFFICIENT
50 Videos
- LAWS OF MOTION BOOK - VMC MODULES ENGLISHCHAPTER - LAWS OF MOTION EXERCISE - IMPECCABLE
53 Videos
- LAWS OF MOTION BOOK - VMC MODULES ENGLISHCHAPTER - LAWS OF MOTION EXERCISE - IMPECCABLE
53 Videos
- KINEMATICS OF A PARTICLE BOOK - VMC MODULES ENGLISHCHAPTER - KINEMATICS OF A PARTICLE EXERCISE - JEE Advanced (archive)
14 Videos
- LIQUIDSBOOK - VMC MODULES ENGLISHCHAPTER - LIQUIDSEXERCISE - JEE ADVANCED (LEVEL -2)
55 Videos
Similar Questions
A block of mass m rests on a fixed incline plane of inclination θ with horizontal Assume friction is large enough to make the block stationary. Then choose correct alternative (s)
View SolutionA horizontal force F pushes wedge of mass M on a smooth horizontal surface. A block of mass m is stationary to the wedge, then:
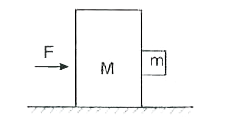
View SolutionA block of mass m rests on a stationary wedge of mass M. The wedge can slide freely on a smooth horizontal surface as shown in figure. If the block starts from rest

View SolutionA block of mass 2 kg rests on a rough inclined plane making an angle of 30° with the horizontal. If μS=0.6 , what is the frictional force on the block ?
View SolutionTwo blocks of masses m and m' are connected by a light spring on a horizontal frictionless table . The spring is compressed and then released . Find the ratio of acceleration of masses .
View SolutionA block of mass m is placed at rest on a smooth wedge of mass M placed at rest on a smooth horizontal surface. As the system is released

View SolutionBy what acceleration the boy must go up so that 100kg block remains stationary on the wedge. The wedge is fixed and is smooth (g=10m/s2)
 .
.
View SolutionA block of mass m1 rests on a horizontal table. A string tied to the block is passed on a frictionless pulley fixed at the end of the table and to the other end of string is hung another block of mass m2. The acceleration of the system is
View SolutionA block of mass 1 kg is at rest relative to a smooth wedge moving leftwards with constant accelerationa=5m/s2 Let N be the normal reaction between block and the wedge .Then (g=10m/s2)

View SolutionA triangular prism of mass m placed on it is released from rest on a smooth inclined plane of inclination θ The block does not slip on the prism. Then
View Solution
