Which is true for rolling friction (μr), static friction (μs) and kinetic friction (μk) ?
(a)μs>μk>μr
(b)μs<μk<μr
(c)μs<μk>μr
(d)μs>μk>μr
The correct Answer is:1
To solve the question regarding the relationship between rolling friction (μ_r), static friction (μ_s), and kinetic friction (μ_k), let's analyze the properties of these types of friction step by step.
1. Understanding Friction Types:
- Static Friction (μ_s): This is the friction that prevents an object from starting to move. It acts when a force is applied to an object at rest.
- Kinetic Friction (μ_k): This is the friction that acts on an object that is already in motion. It is usually less than static friction.
- Rolling Friction (μ_r): This is the friction that occurs when an object rolls over a surface. It is generally the least among the three types of friction.
2. Comparing the Magnitudes:
- It is known from physics that:
- The maximum static friction (μ_s) is greater than kinetic friction (μ_k) when an object is in motion.
- Kinetic friction (μ_k) is greater than rolling friction (μ_r) when an object rolls.
- Therefore, we can establish the following inequality:
μs>μk>μr
3. Conclusion:
- Based on the above comparison, we can conclude that the relationship among the coefficients of friction is:
μs>μk>μr
- This means that static friction is the greatest, followed by kinetic friction, and rolling friction is the least.
Final Answer:
The correct statement is: μ_s > μ_k > μ_r.
- Static Friction (μ_s): This is the friction that prevents an object from starting to move. It acts when a force is applied to an object at rest.
- Kinetic Friction (μ_k): This is the friction that acts on an object that is already in motion. It is usually less than static friction.
- Rolling Friction (μ_r): This is the friction that occurs when an object rolls over a surface. It is generally the least among the three types of friction.
- It is known from physics that:
- The maximum static friction (μ_s) is greater than kinetic friction (μ_k) when an object is in motion.
- Kinetic friction (μ_k) is greater than rolling friction (μ_r) when an object rolls.
- Therefore, we can establish the following inequality:
μs>μk>μr
- Based on the above comparison, we can conclude that the relationship among the coefficients of friction is:
μs>μk>μr
- This means that static friction is the greatest, followed by kinetic friction, and rolling friction is the least.
The correct statement is: μ_s > μ_k > μ_r.
Topper's Solved these Questions
- LAWS OF MOTION BOOK - VMC MODULES ENGLISHCHAPTER - LAWS OF MOTION EXERCISE - IMPECCABLE
53 Videos
- LAWS OF MOTION BOOK - VMC MODULES ENGLISHCHAPTER - LAWS OF MOTION EXERCISE - ENABLE
50 Videos
- KINEMATICS OF A PARTICLE BOOK - VMC MODULES ENGLISHCHAPTER - KINEMATICS OF A PARTICLE EXERCISE - JEE Advanced (archive)
14 Videos
- LIQUIDSBOOK - VMC MODULES ENGLISHCHAPTER - LIQUIDSEXERCISE - JEE ADVANCED (LEVEL -2)
55 Videos
Similar Questions
Static friction is more than sliding friction.
View SolutionDefine the coefficient of static friction and kinetic friction.
View SolutionA box of mass 200 kg is kept on a rough horizontal floor having coefficient of static friction μs=0.25 and coefficient kinetic friction μk=0.2. Find the work done by a man to slide the body slowly through 20 m with a minimum force. Also find the magnitude of the minimum force.
View SolutionA body of mass 10 kg is kept on a horizontal floor of coefficent of static friction μs=0.5 and coefficient of kinetic friction μk=0.45 as shown in figure.
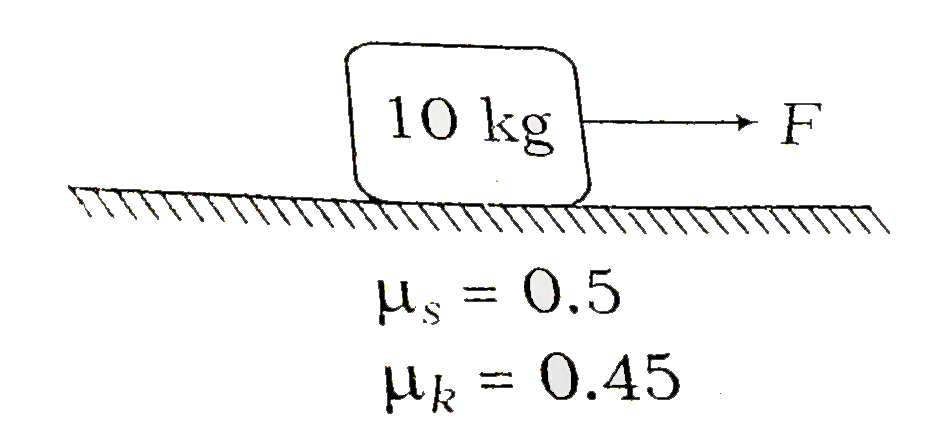
Find the acceleration, force of friction and contact force on the body by the plane when the driving force is (g=10ms−2)
(i) 40 N (ii)60N
View SolutionDifference between Static friction and sliding friction
View SolutionA block of mass m rests on a rough horizontal plane having coefficient of kinetic friction μk and coefficient of static friction μs. The spring is in its natural, when a constant force of magnitude P=5μkmg4 starts acting on the block. The spring force F is a function of extension x as F=kx2.( Where k is spring constant )

(a) Comment on the relation between μs and μk for the motion to start.
(b) Find the maximum extension in the spring ( Assume the force P is sufficient make the block move ).
View SolutionA block with mass m1 is placed on an inclined plane with slope angle α and is connected to a second hunging block with mass m2 by a cord passing over a small . Friction less pulley as shown in fig 7.247 . The coefficient of static friction is μ2 and the coefficient of kinetic friction is μs

a. Find the mass m2 for which block m1 moves up plane at constant speed once it is set in motion
b. Find the mass m2 for which block m1 moves down the plane at constant speed once it is set in motion
c.For what range of m2 will the blocks remain at rest if they are released from rest?
View SolutionLet as consider the next case in the previous illustration when there is no friction between ground and M . The coefficient of static and kinetic friction are μ2 and μ1, respectively, and force F acts upper block as shown in figure
a. What is the maximum possible value of F so that the system moves together ?
b . If there is releative sliding between M and m then calculate acceleration of M and m

View SolutionA small coin of mass 80g is placed on the horizontal surface of a rotating disc. The disc starts from rest and is given a constant angular acceleration α=2rad/s2. The coefficient of static friction between the coin and the disc is μs=3/4 and cofficient of kinetic friction is μk=0.5. The coin is placed at a distance r=1m from the centre of the disc. The magnitude of the resultant force on the coin exerted by the disc just before it starts slipping on the disc is

View SolutionA small coin of mass 80g is placed on the horizontal surface of a rotating disc. The disc starts from rest and is given a constant angular acceleration α=2rad/s2. The coefficient of static friction between the coin and the disc is μs=3/4 and cofficient of kinetic friction is μk=0.5. The coin is placed at a distance r=1m from the centre of the disc. The magnitude of the resultant force on the coin exerted by the disc just before it starts slipping on the disc is

View Solution
