The work done in pushing a block of mass 10 kg from bottom to the top of a frictionless inclined plane 5 m long and 3 m high is-
(g=9.8m/sec2)
392 J
294 J
98 J
0.98 J
The correct Answer is:B
To solve the problem of calculating the work done in pushing a block of mass 10 kg from the bottom to the top of a frictionless inclined plane that is 5 m long and 3 m high, we can follow these steps:
Step 1: Identify the parameters
- Mass of the block (m) = 10 kg
- Height of the inclined plane (h) = 3 m
- Acceleration due to gravity (g) = 9.8 m/s²
Step 2: Calculate the work done
Since the inclined plane is frictionless, the work done on the block is equal to the change in potential energy as it is raised to a height h. The formula for gravitational potential energy (PE) is given by:
PE=m⋅g⋅h
Step 3: Substitute the values into the formula
Now, substituting the known values into the potential energy formula:
PE=10kg⋅9.8m/s2⋅3m
Step 4: Perform the multiplication
Calculating the above expression step by step:
1. First, calculate 10⋅9.8:
10⋅9.8=98kg m/s2
2. Now, multiply this result by the height (3 m):
98⋅3=294Joules
Step 5: Conclusion
Thus, the work done in pushing the block to the top of the inclined plane is:
Work Done=294Joules
Final Answer
The work done in pushing the block is 294 Joules.
---
- Mass of the block (m) = 10 kg
- Height of the inclined plane (h) = 3 m
- Acceleration due to gravity (g) = 9.8 m/s²
Since the inclined plane is frictionless, the work done on the block is equal to the change in potential energy as it is raised to a height h. The formula for gravitational potential energy (PE) is given by:
Now, substituting the known values into the potential energy formula:
Calculating the above expression step by step:
Thus, the work done in pushing the block to the top of the inclined plane is:
The work done in pushing the block is 294 Joules.
Topper's Solved these Questions
- WORK ENERGY AND POWER BOOK - VMC MODULES ENGLISHCHAPTER - WORK ENERGY AND POWER EXERCISE - ENABLE
50 Videos
- WORK ENERGY AND POWER BOOK - VMC MODULES ENGLISHCHAPTER - WORK ENERGY AND POWER EXERCISE - EFFICIENT
50 Videos
- WAVE MOTIONBOOK - VMC MODULES ENGLISHCHAPTER - WAVE MOTIONEXERCISE - JEE ADVANCED ARCHIVE LEVEL 2 (TRUE FALSE TYPE)
4 Videos
Similar Questions
A person pushes a block of mass 4 kg up a frictionless inclined plane 10 m long and that makes an angle of 30∘ with the horizontal . Then the work done is
View SolutionA block of mass 'm' is released on the top of a frictionless incline as shown in the figure. The time period of the oscillation of the block is

View Solution
Knowledge Check
Two blocks each of mass M are resting on a frictionless inclined plane as shown in fig then:
 AThe block A moves down the planeBThe block B moves down the plane.CBoth the blocks remain at restDBoth the blocks move down the plane.
AThe block A moves down the planeBThe block B moves down the plane.CBoth the blocks remain at restDBoth the blocks move down the plane.
A block of mass 2kg is released from rest on a rough inclined ground as shown in figure. Find the work done on the block by a) gravity b) force of friction .when the block is displaced downward along the plane by 2m ?
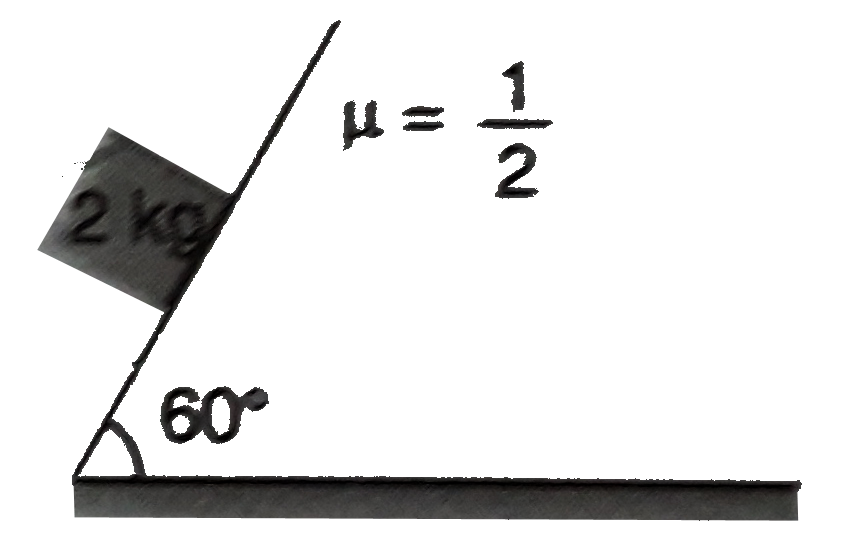 .
.
(Take g10m/s2).
View SolutionA cart of mass 0.5kg is placed on a smooth surface and is connected by a string to a block of mass 0.2kg. At the initial moment the cart moves to the left along a horizontal plane at a speed of 7m/s(Use g=9.8m/s2)
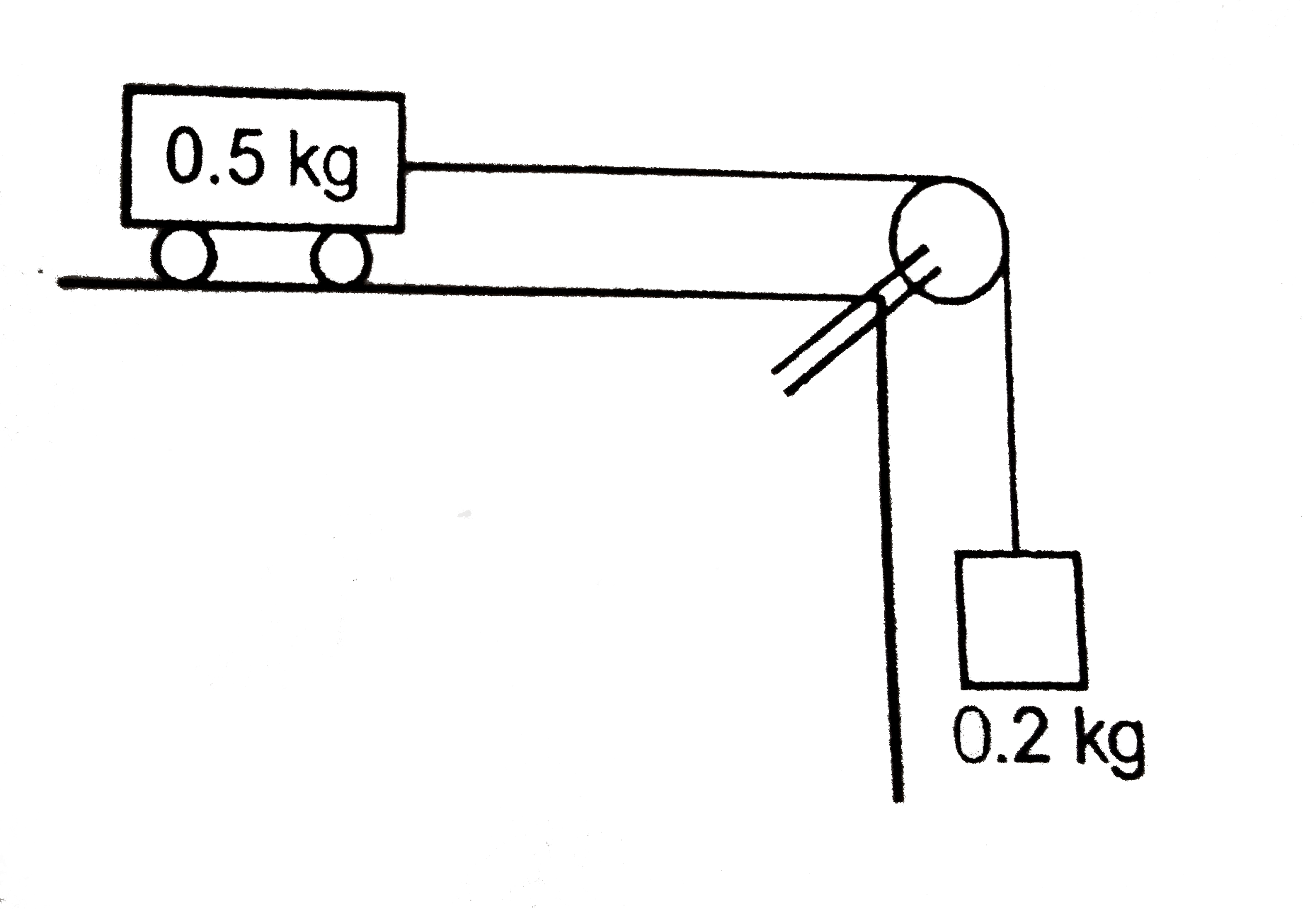
View SolutionA body of mass 10 kg is dropped to the ground from a height of 10 metres. The work done by the gravitational force is (g=9.8m/sec2)
View SolutionThe coefficient of friction between a body of mass 1kg and the surface of an inclined plane at 45∘ is 0.5. if g=9.8m/s2, the acceleration of the body downwards in m/s2 is
View SolutionA wire of 9.8×10−3kgm passes over a frictionless light pulley fixed on the top of a frictionless inclined plane which makes an angle of 30∘ with the horizontal. Masses m and M are tied at the two ends of wire such that m rests on the plane and M hangs freely vertically downwards. the entire system is in equilibrium and a transverse wave propagates along the wire with a velocities of 100m/s.
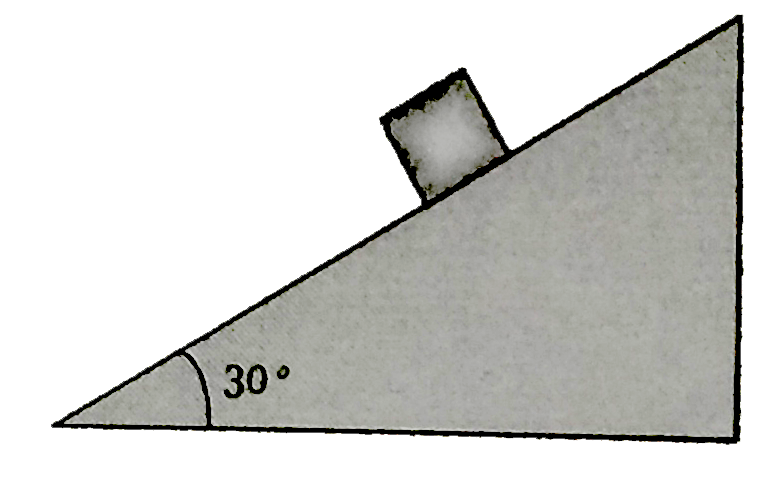
View SolutionThe time taken by a block of wood (initially at rest) to slide down a smooth inclined plane 9.8 m long (angle of inclination is 30∘) is
View SolutionA man weighing 70 kg carries a 30 kg box to the top of a building 20 m high. Calculate the work done by the man (take g=9.8ms−2).
View Solution
