A rod of length L and mass m is kept vertically on the ground. Its potential energy is :
(a)mgL
(b)mg.L2
(c)mg.L3
(d)mg.L4
The correct Answer is:B
To find the potential energy of a rod of length L and mass m kept vertically on the ground, we can follow these steps:
1. Understand the Concept of Potential Energy:
The potential energy (PE) of an object is given by the formula:
PE=mgh
where m is the mass of the object, g is the acceleration due to gravity, and h is the height of the center of mass above a reference point (in this case, the ground).
2. Identify the Height of the Center of Mass:
For a uniform rod of length L, the center of mass is located at the midpoint of the rod. Therefore, the height h of the center of mass above the ground is:
h=L2
3. Substitute Values into the Potential Energy Formula:
Now, substituting the values of m, g, and h into the potential energy formula:
PE=mg(L2)
4. Simplify the Expression:
This simplifies to:
PE=mgL2
5. Conclusion:
Thus, the potential energy of the rod is:
PE=mgL2
Final Answer:
The potential energy of the rod is mgL2.
The potential energy (PE) of an object is given by the formula:
PE=mgh
where m is the mass of the object, g is the acceleration due to gravity, and h is the height of the center of mass above a reference point (in this case, the ground).
For a uniform rod of length L, the center of mass is located at the midpoint of the rod. Therefore, the height h of the center of mass above the ground is:
h=L2
Now, substituting the values of m, g, and h into the potential energy formula:
PE=mg(L2)
This simplifies to:
PE=mgL2
Thus, the potential energy of the rod is:
PE=mgL2
The potential energy of the rod is mgL2.
Topper's Solved these Questions
Similar Questions
A rod AC of length l and mass m is kept on a horizontal smooth plane. It is free to rotate and move. A particle of same mass m moving on the plane with velocity v strikes the rod at point B making angle 37∘ with the rod. The collision is elastic. After collision,

View SolutionA rod of mass M and length L is made to stand vertically. Potential energy of the rod in this position is
View SolutionA thin uniform rod of length l and mass m is freely pivoted about its end. The rod is initially held horizontally and released from rest. When the rod is vertical, an impulse J is applied to bring it to rest (this is in addition to any impulse provided by the pivot)

What is the angular velocity of the rod at the moment it reaches the vertical position ?
View SolutionA uniform rod of length l and mass m is free to rotate in a vertical plane about A as shown in Fig. The rod initially in horizontal position is released. The initial angular acceleration of the rod is

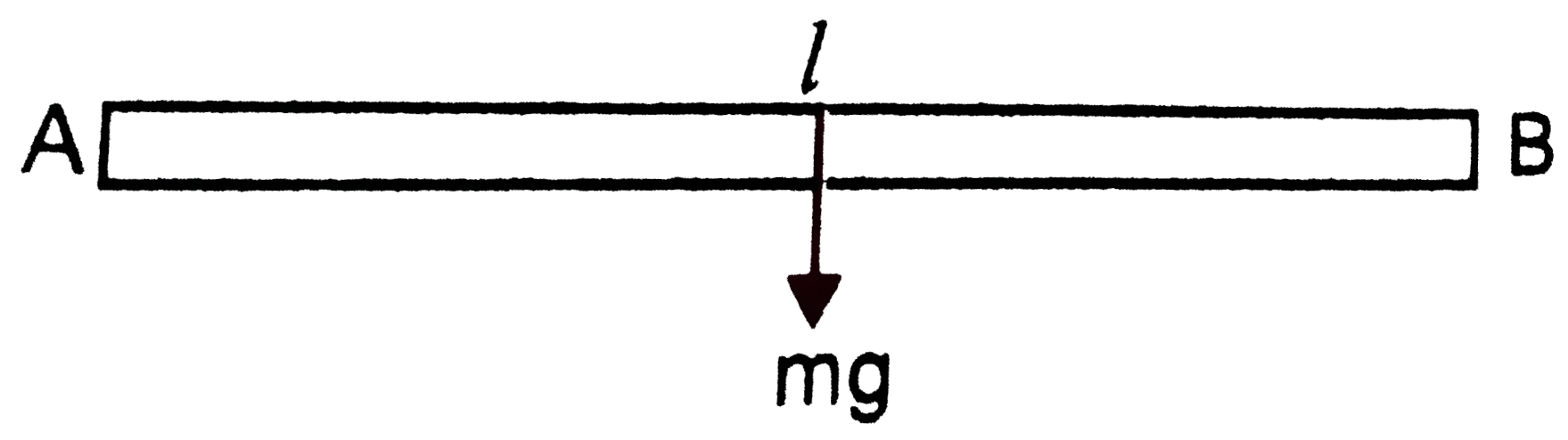
View SolutionIn the figure shown a uniform rod of length l and mass m is kept at rest in horizontal position on an elevated edge. The value of x is such that the rod will have maximum angular acceleration α, as soon as it is set free.
View SolutionA unifrom rod of length l and mass m is free to rotate in a vertical plane about A, Fig. The rod initially in horizontal position is released. The initial angular acceleration of the rod is (MIof rod aboutAisml23)
View SolutionA particle of mass m is fixed to one end of a light rigid rod of length l and rotated in a vertical ciorcular path about its other end. The minimum speed of the particle at its highest point must be
View SolutionA rod of length 2 m is kept vertical inside a smooth spherical shell of radius 2m. The rod starts slipping inside the shell . Mass of the rod is 4 kg.
Velocity of centre of the rod (in m/s) at the instant is approximately

View Solution
A uniform rod of length 4l and mass m is free to rotate about a horizontal axis passing through a point distant l from its one end. When the rod is horizontal its angular velocity is ω as shown in figure. calculate
(a). reaction of axis at this instant,
(b). Acceleration of centre of mass of the rod at this instant.
(c). reaction of axis and acceleration of centre mass of the rod when rod becomes vertical for the first time.
(d). minimum value of ω, so that centre of rod can complete circular motion.
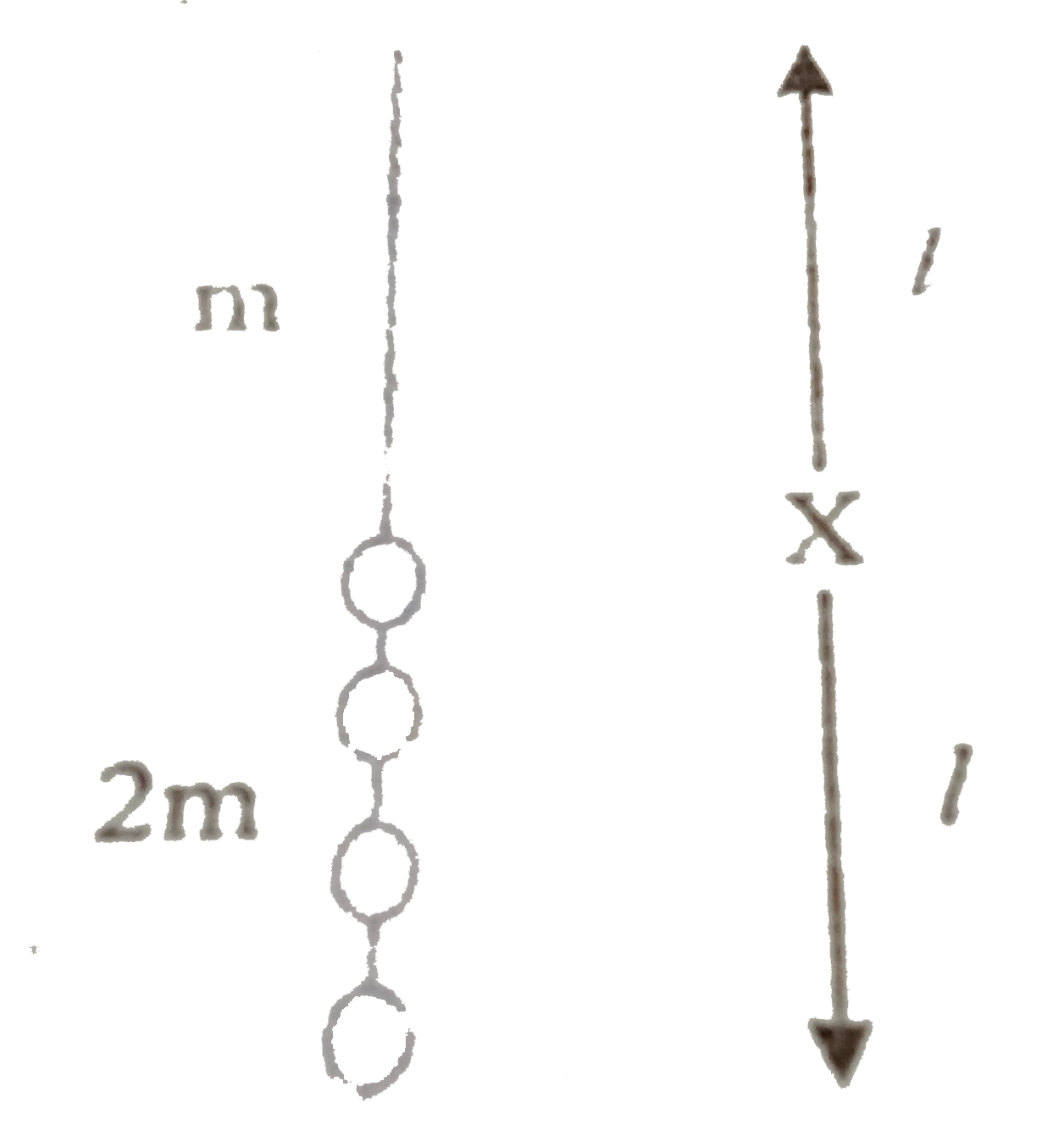
View SolutionA rope of length l and mass 'm' is connected to a chain of length l and mass 2m and hung vertically as shown. What is the change in graviational potential energy if the system is inverted and hung from same point.
 .
.
View Solution
