A spring is held compressed so that its stored energy is 2.4J. Its ends are in constant with masses 1gand48g placed on a friction less table. When the spring in released, the heavier mass will acquire a speed of:
240149m/s
24×4948m/s
107m/s
1047m/s
The correct Answer is:C
To solve the problem, we will use the principles of conservation of energy and conservation of momentum.
1. Identify the Given Data:
- Stored energy in the spring (E) = 2.4 J
- Mass of the first object (m1) = 1 g = 0.001 kg
- Mass of the second object (m2) = 48 g = 0.048 kg
2. Use Conservation of Energy:
When the spring is released, the potential energy stored in the spring is converted into the kinetic energy of the two masses.
E=12m1v21+12m2v22
Substituting the value of E:
2.4=12(0.001)v21+12(0.048)v22
Simplifying, we get:
2.4=0.0005v21+0.024v22(Equation 1)
3. Use Conservation of Momentum:
Since the initial velocities are zero, the momentum before release is zero. Therefore, the momentum after release must also be zero:
m1v1+m2v2=0
This implies:
m1v1=−m2v2⇒v1=−m2m1v2
Substituting the values of m1 and m2:
v1=−0.0480.001v2=−48v2(Equation 2)
4. Substituting Equation 2 into Equation 1:
Substitute v1=−48v2 into Equation 1:
2.4=0.0005(−48v2)2+0.024v22
Simplifying:
2.4=0.0005×2304v22+0.024v22
2.4=1.152v22+0.024v22
2.4=1.176v22
5. Solving for v22:
v22=2.41.176≈2.04
v2=√2.04≈1.43m/s
Final Answer:
The speed of the heavier mass (48 g) when the spring is released is approximately 1.43 m/s.
- Stored energy in the spring (E) = 2.4 J
- Mass of the first object (m1) = 1 g = 0.001 kg
- Mass of the second object (m2) = 48 g = 0.048 kg
When the spring is released, the potential energy stored in the spring is converted into the kinetic energy of the two masses.
E=12m1v21+12m2v22
Substituting the value of E:
2.4=12(0.001)v21+12(0.048)v22
Simplifying, we get:
2.4=0.0005v21+0.024v22(Equation 1)
Since the initial velocities are zero, the momentum before release is zero. Therefore, the momentum after release must also be zero:
m1v1+m2v2=0
This implies:
m1v1=−m2v2⇒v1=−m2m1v2
Substituting the values of m1 and m2:
v1=−0.0480.001v2=−48v2(Equation 2)
Substitute v1=−48v2 into Equation 1:
2.4=0.0005(−48v2)2+0.024v22
Simplifying:
2.4=0.0005×2304v22+0.024v22
2.4=1.152v22+0.024v22
2.4=1.176v22
v22=2.41.176≈2.04
v2=√2.04≈1.43m/s
The speed of the heavier mass (48 g) when the spring is released is approximately 1.43 m/s.
Topper's Solved these Questions
- WORK ENERGY AND POWER BOOK - VMC MODULES ENGLISHCHAPTER - WORK ENERGY AND POWER EXERCISE - EFFICIENT
50 Videos
- WORK ENERGY AND POWER BOOK - VMC MODULES ENGLISHCHAPTER - WORK ENERGY AND POWER EXERCISE - IMPECCABLE
54 Videos
- WORK ENERGY AND POWER BOOK - VMC MODULES ENGLISHCHAPTER - WORK ENERGY AND POWER EXERCISE - IMPECCABLE
54 Videos
- WAVE MOTIONBOOK - VMC MODULES ENGLISHCHAPTER - WAVE MOTIONEXERCISE - JEE ADVANCED ARCHIVE LEVEL 2 (TRUE FALSE TYPE)
4 Videos
Similar Questions
A spring with spring constaant k when compressed by 1 cm the PE stored is U. If it is further compressed by 3 cm, then change in its PE is
View SolutionA spring with spring constaant k when compressed by 1 cm the PE stored is U. If it is further compressed by 3 cm, then change in its PE is
View Solution
Knowledge Check
A spring is compressed by a ping pong ball of mass 100g. On its release it flies with a velocity of 20ms−1. Find the elastic potential energy possessed by spring.
A200JB20JC2000JD2J
The block of mass m is released when the spring was in its natrual length. Spring constant is k. Find the maximum elongation of the spring.

View SolutionA spring is kept compressed by a toy cart of mass 150 g.On releasing the cart.It moves with a speed of 0.2 ms−1 .Calculate the potential energy (elastic)of the spring .
View SolutionA small block of mass 100 g is pressed again a horizontal spring fixed at one end to compress the sprign through 5.0 cm. The spring constant is 100 N/m. When released, the block moves hroizontally till it leaves the spring. Where will it hit the ground 2 m below the spring?
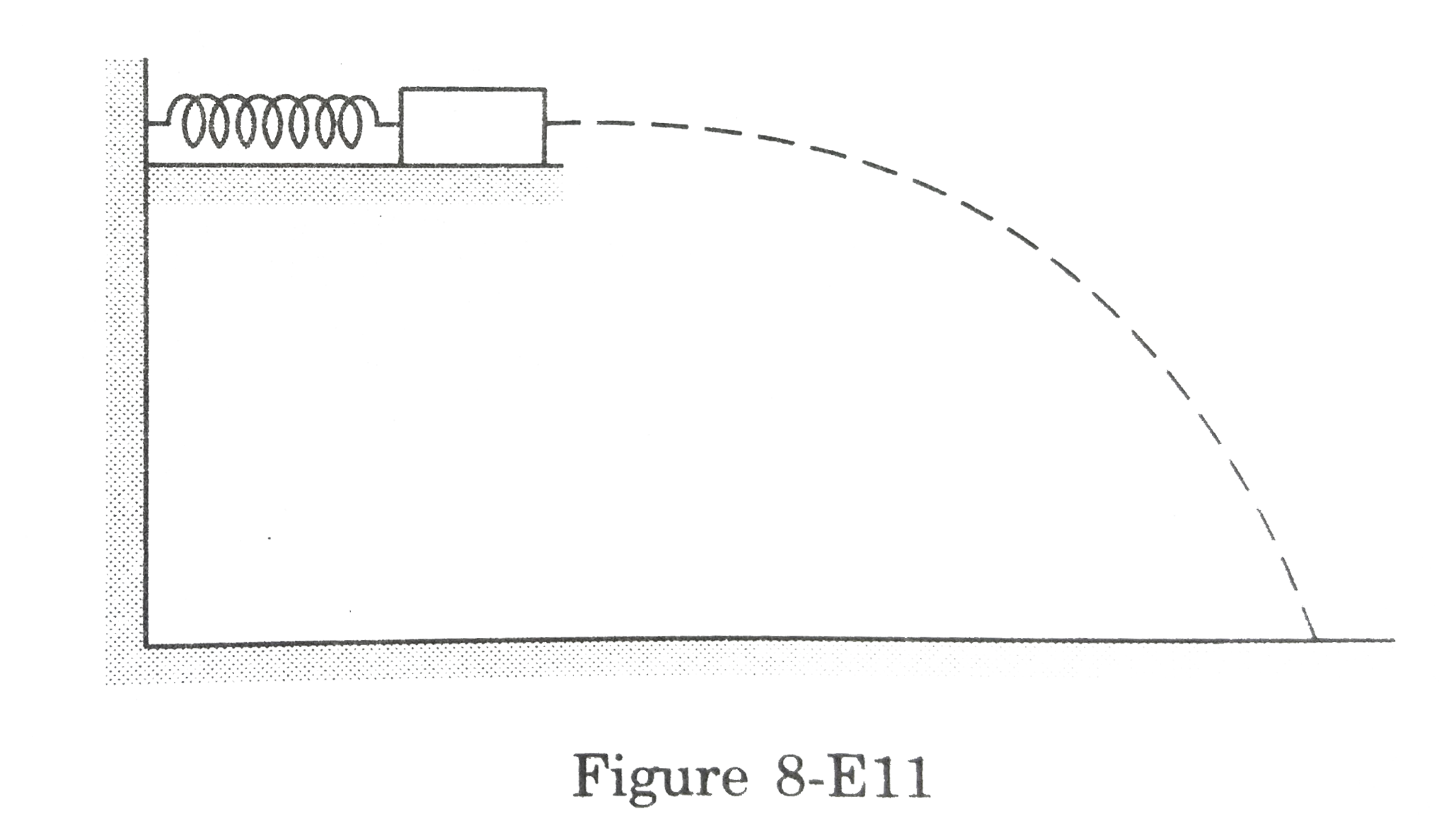
View SolutionConsider the system shown below, with two equal masses m and a spring with spring constant K. The coefficient of friction between the left mass and horizontal table is μ=1/4, and the pulley is frictionless. The spring connecting both the blocks is massless and inelastic. The system is held with the spring at its unstretched length and then released.
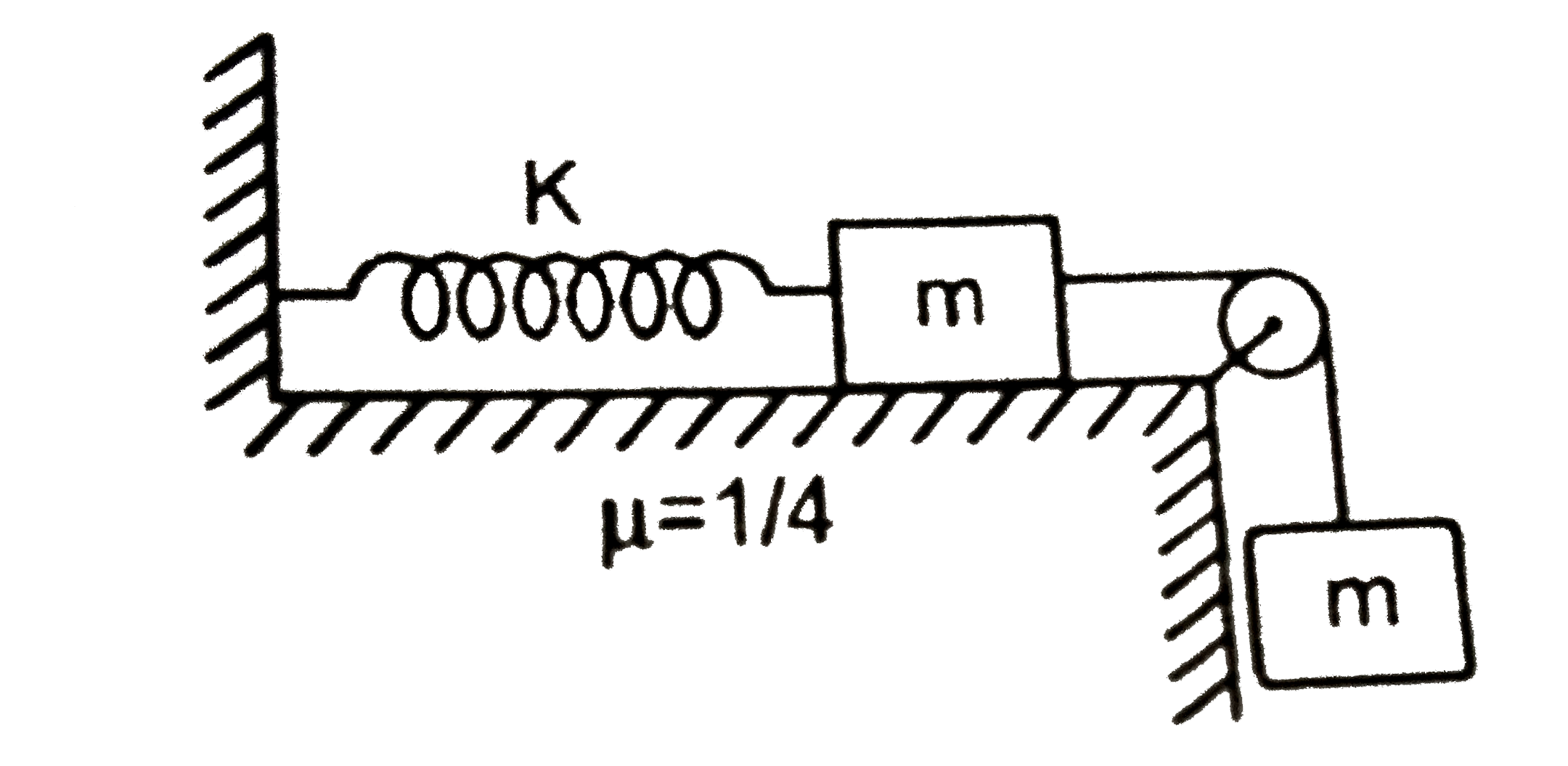
The extension in spring when the masses come to momentary rest for the first time is
View SolutionA spring is kept compressed by a small trolley of mass ring 0-5 kg lying on a smooth horizontal surface as shown in the adjacent Fig. When the trolley is released, it is found to move at a speed = 2 m s−1. What potential energy did the spring poses when compressed?

View Solution
A block of mass m is pushed against a spring of spring constant k fixed at one end to a wall.The block can slide on a frictionless table as shown in the figure. The natural length of the spring is L0 and it is compressed to one fourth of natural length and the block is released.Find its velocity as a function of its distance (x) from the wall and maximum velocity of the block. The block is not attached to the spring.
View SolutionA block of mass m is initially moving to the right on a horizontal frictionless surface at a speed v. It then compresses a spring of spring constant k. At the instant when the kinetic energy of the block is equal to the potential energy of the spring, the spring is compressed a distance of :
View Solution
