Find the centre of mass of the shaded portion of a disc.
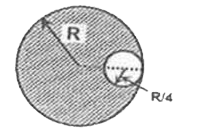
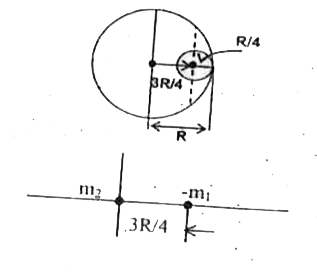
Xcm=m2(0)−m1(3R4)m2−m1=−3R4(m2m1−1)
where m2m1=(πR2)ρπ(R4)2ρ=16
⇒Xcm=−3R4(16−1)=−R20
Note : Negative mass is taken because the mass is removed.
Similar Questions
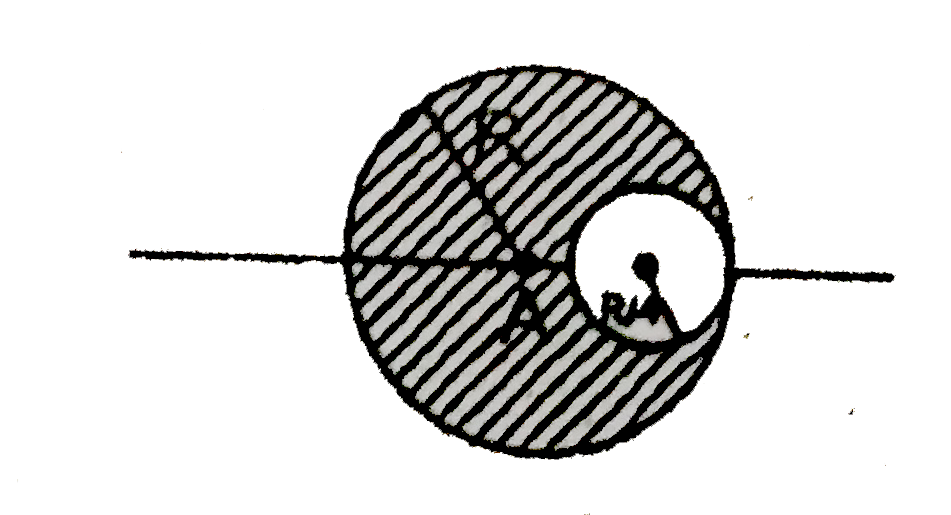
The centre of mass of the shaded portion of the disc is: ( The mass is uniformly distributed in the shaded portion).
View SolutionThe centre of mass of the shaped portion of the disc is (The mass is uniformly distributed in the shaded portion)
View SolutionFigure-4.11 shows a circular a disc of radius R from which a small disc is cut such that the periphery of the small disc touch the large disc and whose radius is R/2. Find the centre of mass of the remaining part of the disc.
View SolutionFind the centre of mass of a uniform disc of radius a from which a circualr section of radius b has been removed. The centre of hole is at a distance c from the centre of the disc.
View SolutionFind the area of the shaded portion in each of the following diagrams :
View SolutionFind the area of the shaded portion in each of the following diagrams :
View SolutionIn the adjoining figure, two circles cut at A and B. P and Q are the centres of the circles. If ∠APB=90∘and∠AQB=60∘, then find the area of the shaded portion if AP = 4 cm. (Use =√3=1.73)
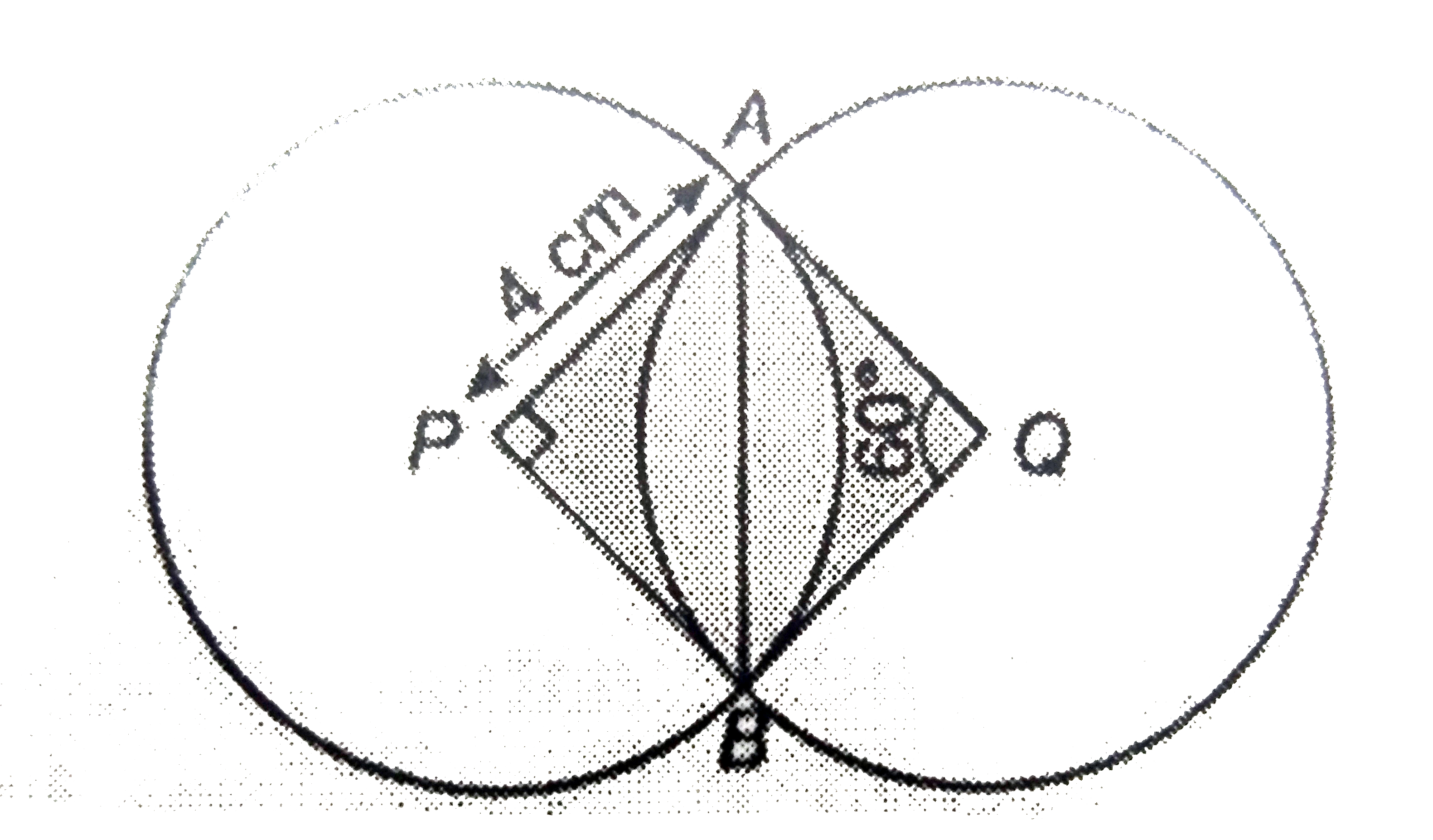View SolutionA square plate of edge a/2 is cut out from a uniform square plate of edge 'a' shown in figure. The mass of the remaining portion is M. The moment of inertia of the shaded portion about an axis passing through 'O'( centre of the square of side a) and perpendicular to plane of the plate is :
View SolutionA disc of mass m and radius R, is placed on a smooth text service fixed surface . Point A is the geometrical centre of the disc while point B is the centre of mass of the disc . The moment of inertia of the dics about an axis through its centre of mass and perpendicular to the plane of the figure is I .A constant force F is applied to the top of the disc . The acceleration of the centre A of the disc at the instant B is below A (on the same vertical line ) will be :
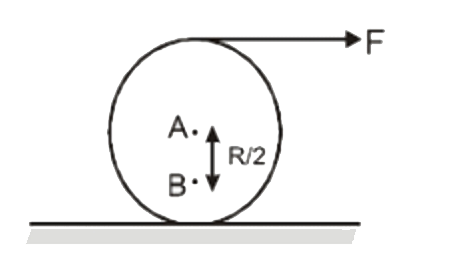View SolutionA uniform solid right circular cone has its base cut out in conical shape shown in figure such that the hollow portion is a right circular cone on the same base. Find what should be the height of the hollow portion so that the centre of mass of the remaining portion may coincide with the vertex of the hollow portion.
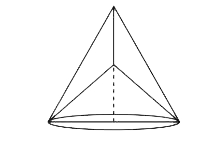View Solution