A gymnast does many acrobats in air before descending on the floor. The quantity conserved, consequent to motion, is:
angular velocity
M.I.
linear momentum
angular momentum
The correct Answer is:D
To solve the question regarding the conservation of quantities during a gymnast's acrobatic movements in the air, we need to analyze the situation with respect to the principles of physics, particularly focusing on angular momentum.
1. Understanding the Motion:
- When a gymnast performs acrobatic movements in the air, they rotate and change their body position. This motion can be analyzed in terms of angular momentum.
2. Angular Momentum Definition:
- Angular momentum (L) is defined as the product of the moment of inertia (I) and the angular velocity (ω):
L=I⋅ω
3. Initial State of the Gymnast:
- Initially, the gymnast has a certain moment of inertia (I) and rotates with an angular velocity (ω). Therefore, the initial angular momentum can be expressed as:
Linitial=I⋅ω
4. Changing Body Position:
- As the gymnast performs acrobats, they may pull their arms and legs closer to their body. This action decreases their moment of inertia (I decreases to I') because the mass distribution is now closer to the axis of rotation.
5. Conservation of Angular Momentum:
- According to the principle of conservation of angular momentum, if no external torque acts on the system, the total angular momentum before and after the change must remain constant:
Linitial=Lfinal
- This means:
I⋅ω=I′⋅ω′
- Here, I' is the new moment of inertia after the gymnast pulls in their limbs, and ω' is the new angular velocity.
6. Effect of Decreased Moment of Inertia:
- Since I' < I, to keep the angular momentum constant, the angular velocity must increase (ω' > ω). This results in the gymnast spinning faster.
7. Conclusion:
- The quantity that is conserved during the gymnast's motion is angular momentum. This conservation allows the gymnast to control their rotation speed and perform various acrobatic maneuvers effectively.
Final Answer:
The quantity conserved, consequent to motion, is angular momentum.
- When a gymnast performs acrobatic movements in the air, they rotate and change their body position. This motion can be analyzed in terms of angular momentum.
- Angular momentum (L) is defined as the product of the moment of inertia (I) and the angular velocity (ω):
L=I⋅ω
- Initially, the gymnast has a certain moment of inertia (I) and rotates with an angular velocity (ω). Therefore, the initial angular momentum can be expressed as:
Linitial=I⋅ω
- As the gymnast performs acrobats, they may pull their arms and legs closer to their body. This action decreases their moment of inertia (I decreases to I') because the mass distribution is now closer to the axis of rotation.
- According to the principle of conservation of angular momentum, if no external torque acts on the system, the total angular momentum before and after the change must remain constant:
Linitial=Lfinal
- This means:
I⋅ω=I′⋅ω′
- Here, I' is the new moment of inertia after the gymnast pulls in their limbs, and ω' is the new angular velocity.
- Since I' < I, to keep the angular momentum constant, the angular velocity must increase (ω' > ω). This results in the gymnast spinning faster.
- The quantity that is conserved during the gymnast's motion is angular momentum. This conservation allows the gymnast to control their rotation speed and perform various acrobatic maneuvers effectively.
The quantity conserved, consequent to motion, is angular momentum.
Topper's Solved these Questions
- SYSTEM OF PARTICLES AND ROTATIONAL MOTIONBOOK - VMC MODULES ENGLISHCHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - IMPECCABLE
56 Videos
- SYSTEM OF PARTICLES AND ROTATIONAL MOTIONBOOK - VMC MODULES ENGLISHCHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - ENABLE
50 Videos
- SYSTEM OF A PARTICLES & ROTATIONAL MOTIONBOOK - VMC MODULES ENGLISHCHAPTER - SYSTEM OF A PARTICLES & ROTATIONAL MOTIONEXERCISE - IN-CHAPTER EXERCISE F
10 Videos
- UNITS, MEASUREMENTS & ERRORSBOOK - VMC MODULES ENGLISHCHAPTER - UNITS, MEASUREMENTS & ERRORSEXERCISE - IN - CHAPTER EXERCISE - B
10 Videos
Similar Questions
The graph as shown in. below descrines the motion of a ball rebounding from a horizontal surface being released from a point above the surface. Assume that the ball colledes each time with the floor inelastically. The quantity represented on the y-axis in the is the balls (take upward direction as positive)
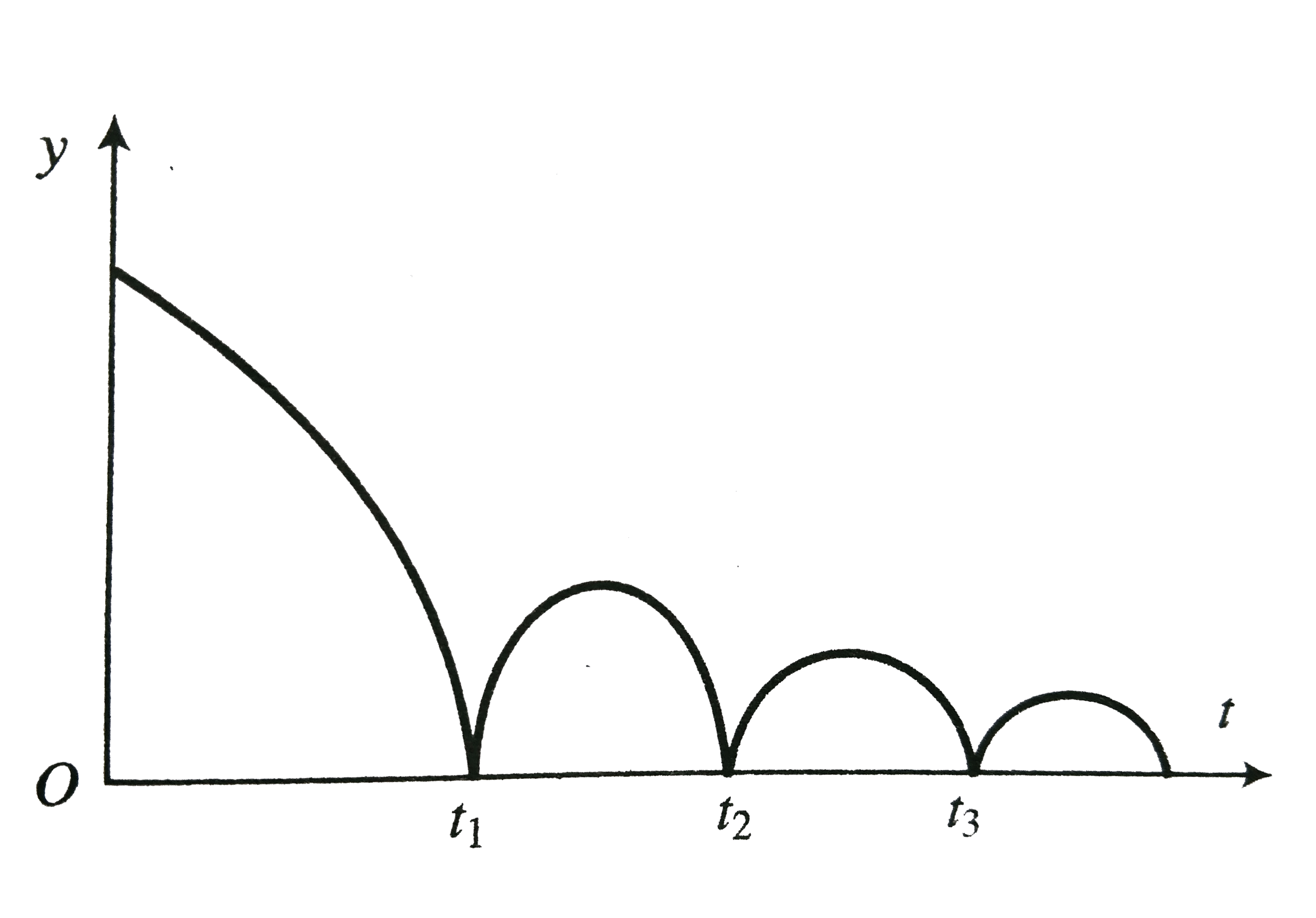 .
.
View SolutionA body explodeds in mid - air. Does its momentum remain conserved ?
View Solution
Knowledge Check
A projectile is fired at an angle θ with the horizontal in a resistance from atmosphere. Which of the following quantities does not change during the motion ?
AMomentumBkinetic energyCvertical component of its velocityDHorizontal component of its velocity
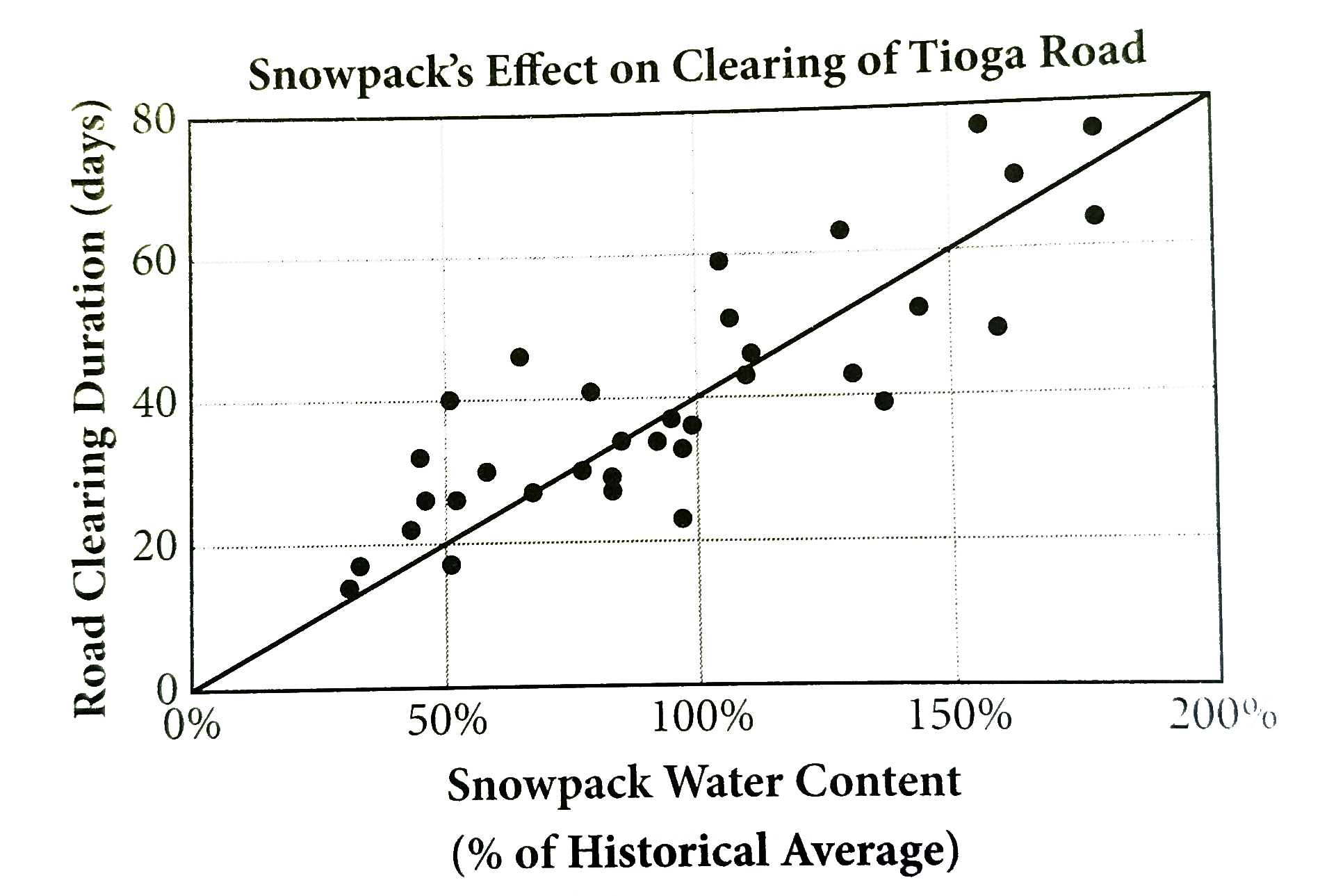
Tioga Road is a mountain pass that crosses the Sierra nevada through northern Yosemite National Park. The road is closed from about November through late May. This time period can change depending on the quantity and nature of the season's snowfall, as well as unforeseen obstacles such as fallen trees or rocks. The scatterplot above compares the snowpack water content on April 1 (for year 1981-2014) as a percent of the historical average to the time it takes th National Park Service to fully clear the road and open it to traffic.
For every 5 percent increases in snowpack water content, how many more days does it take the National Park Service to clear Tioga Road ?
View SolutionAn amusement park ride consist of a large verticle cylinder that spins about its axis first fast enough that any person inside is held up againest the wall when the is μs and the radius of the cylider is R

a. Shown that maximum period of revolation neccessary to keep the person from falling is T=(4π2μsR/g)1/2
b. Obtain a numerical value for T taking R=4.00m and μs=0.400 . How many revolations per minute does the cylinder make?
c. If the rate of revolation of the cylinder is make to be some what larger what happens to the magnitude of each one of the forces acting on the person ? What happens to the motion of the person ?
d. If instead the cylinder rate revolution is made to be somewhat smaller what happens to the magnitude and what happens to the motion of the person ?
View Solution(Answer the following questions briefly and to the point :)
Which physical quantity remains conserved in Simple Harmonic Motion ?
View Solution[A] : Many desert mammals cool the exhaled air in their noses , before it is expelled out through nostrills .
[R] : The moisture condensation in the nose and is not lost as water vapours along with the exhaled air .
View SolutionThe ballon the light rope and the monkey shown in figure are at rest in the air. If the monkey reaches the top of the rope, by what distnce does the ballon descend? Mass of the ballon =M mass of the monkey =m and the length of the rope ascended by the monkey =L
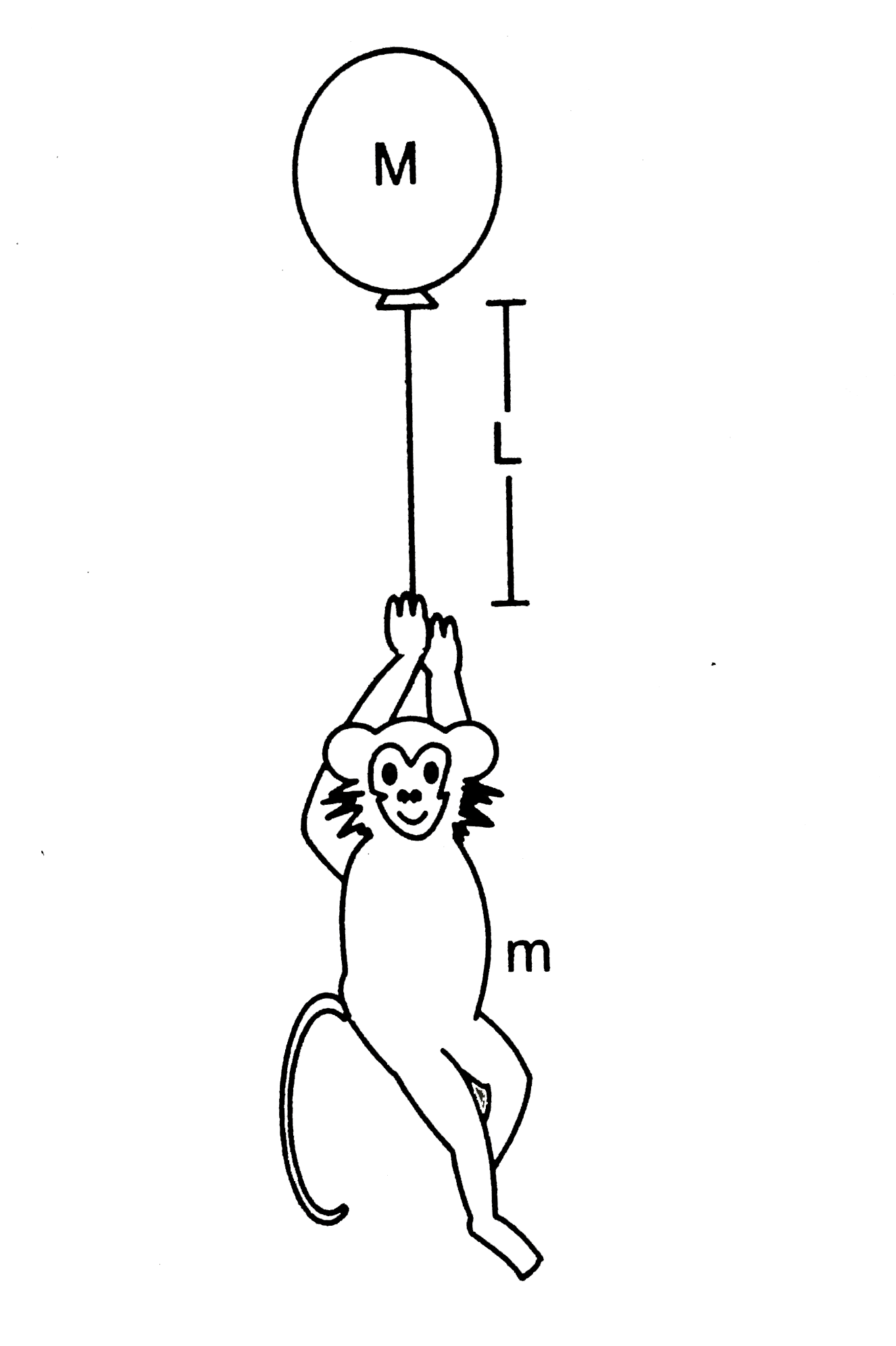
View SolutionUnderline the correct alterntaive:
a) when a conservative force does positivie work on a body, the potential energy of the body increase/decreases/remains unaltered.
work done by a body against friction always results in a loss of its kinetic /potential energy.
c) The rate of change of total momentum of a many-particle system is proportional to the external force/ sum of the internal forces on the system.
d) In an inelastic collision of two bodies, the quantities which do not change after the collision are the total kinetic energy/total linear momentum/total enregy of the system of two bodies.
View SolutionCollision is a physical process in which two or more objects, either particle masses or rigid bodies, experience very high force of interaction for a very small duration. It is not essential for the objects to physically touch each other for collision to occur. Irrespective of the nature of interactive force and the nature of colliding bodies, Newton's second law holds good on the system. Hence, momentum of the system before and after the collision remains conserved if no appreciable external force acts on the system during collision.
The amount of energy loss during collision, if at all, is indeed dependent on the nature of colliding objects. The energy loss is observed to be maximum when objects stick together after collision. The terminology is to define collision as 'elastic' if no energy loss takes place and to define collision as 'plastic' for maximum energy loss. The behaviour of system after collision depends on the position of colliding objects as well. A unidirectional motion of colliding objects before collision can turn into two dimensional after collision if the line joining the centre of mass of the two colliding objects is not parallel to the direction of velocity of each particle before collision. Such type of collision is referred to as oblique collision which may be either two or three dimensional.
According to the definition of collision in paragraph I, which of the following physical process is not a collision?
View Solution
