The instantaneous angular position of a point on a rotating wheel is given by the equation Q(t)=2t3−6t2. The torque on the wheel becomes zero at
t = 1s
t =0.5 s
t = 0.25 s
t=2s
The correct Answer is:2
Step by step video & image solution for The instantaneous angular position of a point on a rotating wheel is given by the equation Q(t) =2t^(3)-6t^(2). The torque on the wheel becomes zero at by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- SYSTEM OF PARTICLES AND ROTATIONAL MOTIONBOOK - VMC MODULES ENGLISHCHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - EFFICIENT
50 Videos
- SYSTEM OF A PARTICLES & ROTATIONAL MOTIONBOOK - VMC MODULES ENGLISHCHAPTER - SYSTEM OF A PARTICLES & ROTATIONAL MOTIONEXERCISE - IN-CHAPTER EXERCISE F
10 Videos
- UNITS, MEASUREMENTS & ERRORSBOOK - VMC MODULES ENGLISHCHAPTER - UNITS, MEASUREMENTS & ERRORSEXERCISE - IN - CHAPTER EXERCISE - B
10 Videos
Similar Questions
The instantaneous angular position of a point on a rotating wheel is given by the equation
θ(t)=2t3−6t2
The torque on the wheel becomes zero at
View SolutionThe angular position of a point over a rotating flywheel is changing according to the relation, θ=(2t3−3t2−4t−5) radian. The angular acceleration of the flywheel at time, t = 1 s is
View Solution
Knowledge Check
The instantaneous angular position of a point on a rotating wheel is given by the equation
θ(t)=2t3−6t2
The torque on the wheel becomes zero at a) t = 1 s b) t = 0.5 s c) t = 0.25 s d) t = 2 sAt = 1 sBt = 0.5 sCt = 0.25 sDt = 2 s
A angular positio of a point on the rim of a rotating wheel is given by θ=4t−3t2+t3 where θ is in radiuans and t is in seconds. What are the angualr velocities at
(a).t=2.0 and
(b). t=4.0s
(c). What is the average angular acceleration for the time interval that begins at t=2.0s and ends at t=4.0s?
(d). What are the instantaneous angular acceleration at the biginning and the end of this time interval?
View SolutionThe position of a particle is given by the equation f(t)=t3−6t2+9t where t is measured in second and s in meter. Find the acceleration at time t. What is the acceleration at 4 s?
View SolutionThe position of a particle moving along x-axis given by x=(−2t3−3t2+5)m. The acceleration of particle at the instant its velocity becomes zero is
View SolutionA boat of mass 300 kg moves according to the equation x=1.2t2−0.2t3. When the force will become zero ?
View SolutionThe variation of angular position θ, of a point on a rotating rigid body, with time t is shown in Fig. Is the body rotating clock wise or anti-clockwise ?
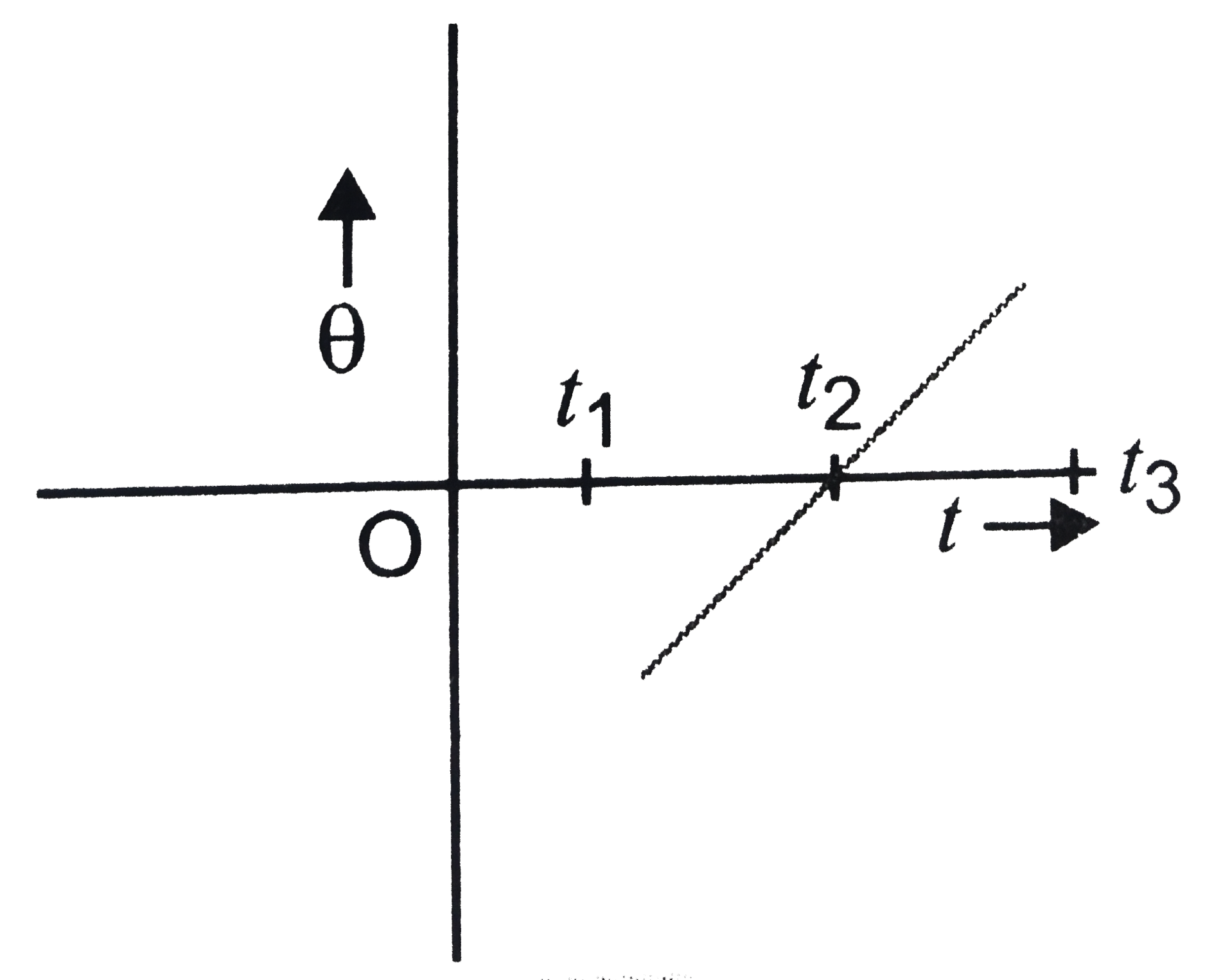
View SolutionThe distances moved by a particle in time t seconds is given by s=t3−6t2−15t+12. The velocity of the particle when acceleration becomes zero, is
View SolutionThe displacement of a particle moving along the x-axis is given by equation x=2t3−21t2+60t+6.The possible acceleration of the particle when its velocity is zero is
View Solution
