There are four rods A, B, C and D of same length L but different linear mass density d, 2d, 3d & 4d respectively. These are joined to form a square frame with sides C & D along x & y axis of coordinate axes respectively. Find coordinate of centre of mass of structure. ?
To find the coordinates of the center of mass of the square frame formed by the four rods A, B, C, and D, we will follow these steps:
Step 1: Identify the Masses of Each Rod
The linear mass densities of the rods are given as follows:
- Rod A: d
- Rod B: 2d
- Rod C: 3d
- Rod D: 4d
Since all rods have the same length L, we can calculate the mass of each rod:
- Mass of Rod A: mA=d⋅L
- Mass of Rod B: mB=2d⋅L
- Mass of Rod C: mC=3d⋅L
- Mass of Rod D: mD=4d⋅L
Step 2: Determine the Coordinates of Each Rod
Assuming the square frame is oriented such that:
- Rod C (length L) is along the x-axis, extending from (0, 0) to (L, 0).
- Rod D (length L) is along the y-axis, extending from (0, 0) to (0, L).
- Rod B is vertical, extending from (L, 0) to (L, L).
- Rod A is horizontal, extending from (0, L) to (L, L).
The coordinates of the center of mass for each rod can be calculated as follows:
- Center of mass of Rod A: (L2,L)
- Center of mass of Rod B: (L,L2)
- Center of mass of Rod C: (L2,0)
- Center of mass of Rod D: (0,L2)
Step 3: Calculate the Total Mass of the System
Total mass M of the system is given by:
M=mA+mB+mC+mD=dL+2dL+3dL+4dL=10dL
Step 4: Calculate the x-coordinate of the Center of Mass
The x-coordinate of the center of mass xcm can be calculated using the formula:
xcm=1M∑(mi⋅xi)
Substituting the values:
xcm=110dL(mA⋅L2+mB⋅L+mC⋅L2+mD⋅0)
=110dL((dL)⋅L2+(2dL)⋅L+(3dL)⋅L2+(4dL)⋅0)
=110dL(dL22+2dL2+3dL22)
=110dL(1dL2+4dL2+3dL22)
=110dL(8dL22)=4L10=2L5
Step 5: Calculate the y-coordinate of the Center of Mass
Similarly, the y-coordinate of the center of mass ycm can be calculated:
ycm=1M∑(mi⋅yi)
Substituting the values:
ycm=110dL(mA⋅L+mB⋅L2+mC⋅0+mD⋅L2)
=110dL((dL)⋅L+(2dL)⋅L2+(3dL)⋅0+(4dL)⋅L2)
=110dL(dL2+dL2+2dL2)=110dL⋅4dL2=4L10=2L5
Final Result
The coordinates of the center of mass of the structure are:
(2L5,2L5)
The linear mass densities of the rods are given as follows:
- Rod A: d
- Rod B: 2d
- Rod C: 3d
- Rod D: 4d
- Mass of Rod A: mA=d⋅L
- Mass of Rod B: mB=2d⋅L
- Mass of Rod C: mC=3d⋅L
- Mass of Rod D: mD=4d⋅L
Assuming the square frame is oriented such that:
- Rod C (length L) is along the x-axis, extending from (0, 0) to (L, 0).
- Rod D (length L) is along the y-axis, extending from (0, 0) to (0, L).
- Rod B is vertical, extending from (L, 0) to (L, L).
- Rod A is horizontal, extending from (0, L) to (L, L).
- Center of mass of Rod A: (L2,L)
- Center of mass of Rod B: (L,L2)
- Center of mass of Rod C: (L2,0)
- Center of mass of Rod D: (0,L2)
Total mass M of the system is given by:
M=mA+mB+mC+mD=dL+2dL+3dL+4dL=10dL
The x-coordinate of the center of mass xcm can be calculated using the formula:
xcm=1M∑(mi⋅xi)
Substituting the values:
xcm=110dL(mA⋅L2+mB⋅L+mC⋅L2+mD⋅0)
=110dL((dL)⋅L2+(2dL)⋅L+(3dL)⋅L2+(4dL)⋅0)
=110dL(dL22+2dL2+3dL22)
=110dL(1dL2+4dL2+3dL22)
=110dL(8dL22)=4L10=2L5
Similarly, the y-coordinate of the center of mass ycm can be calculated:
ycm=1M∑(mi⋅yi)
Substituting the values:
ycm=110dL(mA⋅L+mB⋅L2+mC⋅0+mD⋅L2)
=110dL((dL)⋅L+(2dL)⋅L2+(3dL)⋅0+(4dL)⋅L2)
=110dL(dL2+dL2+2dL2)=110dL⋅4dL2=4L10=2L5
The coordinates of the center of mass of the structure are:
(2L5,2L5)
Topper's Solved these Questions
- BOOK - VMC MODULES ENGLISHCHAPTER - SYSTEM OF A PARTICLES & ROTATIONAL MOTIONEXERCISE - SOLVED EXAMPLES20videos
SYSTEM OF A PARTICLES & ROTATIONAL MOTION
- BOOK - VMC MODULES ENGLISHCHAPTER - SYSTEM OF A PARTICLES & ROTATIONAL MOTIONEXERCISE - PRACTICE EXERCISE-14videos
SYSTEM OF A PARTICLES & ROTATIONAL MOTION
- BOOK - VMC MODULES ENGLISHCHAPTER - SIMPLE HARMONIC MOTION EXERCISE - 7-previous year question46videos
SIMPLE HARMONIC MOTION
- BOOK - VMC MODULES ENGLISHCHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - IMPECCABLE56videos
SYSTEM OF PARTICLES AND ROTATIONAL MOTION
Similar Questions
A ,B and C are the points (2,0),(5,0)and(5,3) respectively. Find coordinates of D such that ABCD is a square.
View SolutionWrite the equation of the plane whose intercepts on the coordinate axes are −4,2and3 respectively.
View SolutionIn ABC, D and E are the mid-points of AB and AC respectively. Find the ratio of the areas of ADE and ABC .
View SolutionIn the arrangement as shown, A and B arc two cylinders each of length L and density d1 and d2(d1<d2) respectively. They are joined together and submerged in the liquid of density d with length L/2 of A outside the liquid. If the difference in densities of two cylinders is equal to density of the liquid, find d1.
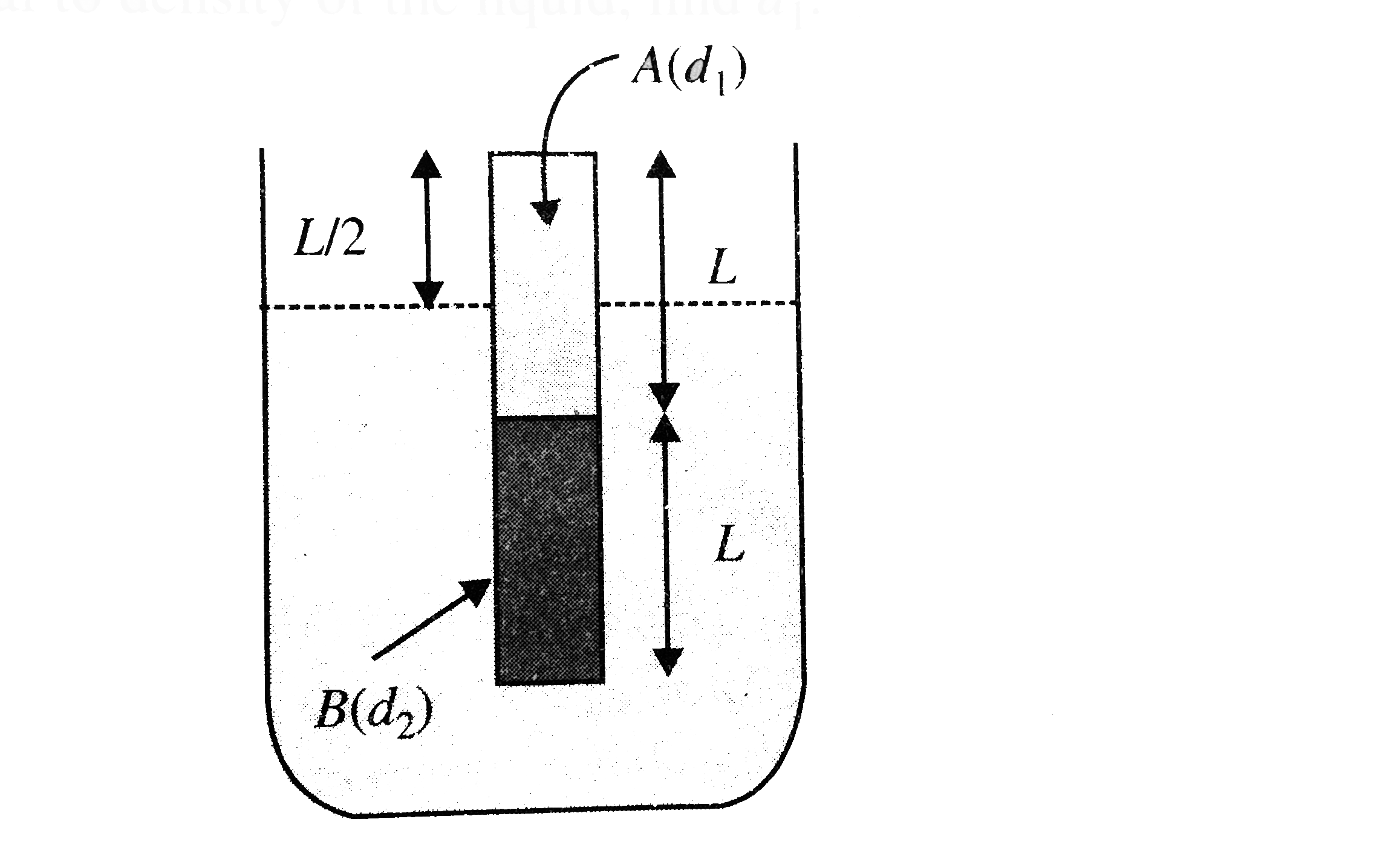 View Solution
View SolutionIn the arrangement as shown, A and B arc two cylinders each of length L and density d1 and d2(d1<d2) respectively. They are joined together and submerged in the liquid of density d with length L/2 of A outside the liquid. If the difference in densities of two cylinders is equal to density of the liquid, find d1.
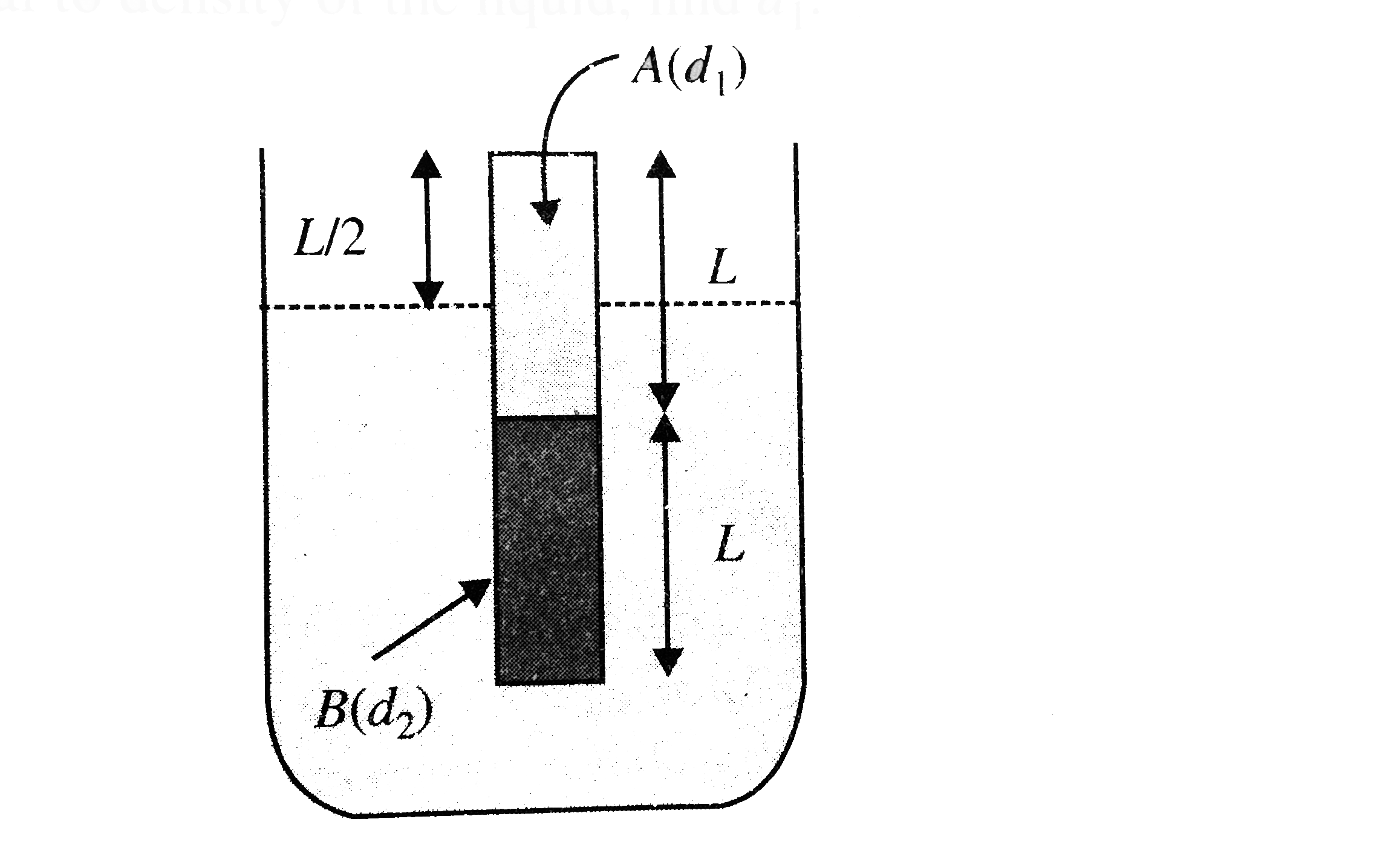 View Solution
View SolutionFour particles of masses 1kg, 2kg, 3kg and 4kg are placed at the four vertices A, B, C and D of a square of side 1m. Find the position of centre of mass of the particles.
View SolutionFour particles of masses 1kg,2kg,3kg and 4kg are placed the four vertices A,B,C and D, respectively, of a square of side 1m. Find the position of centre of mass of the particles.
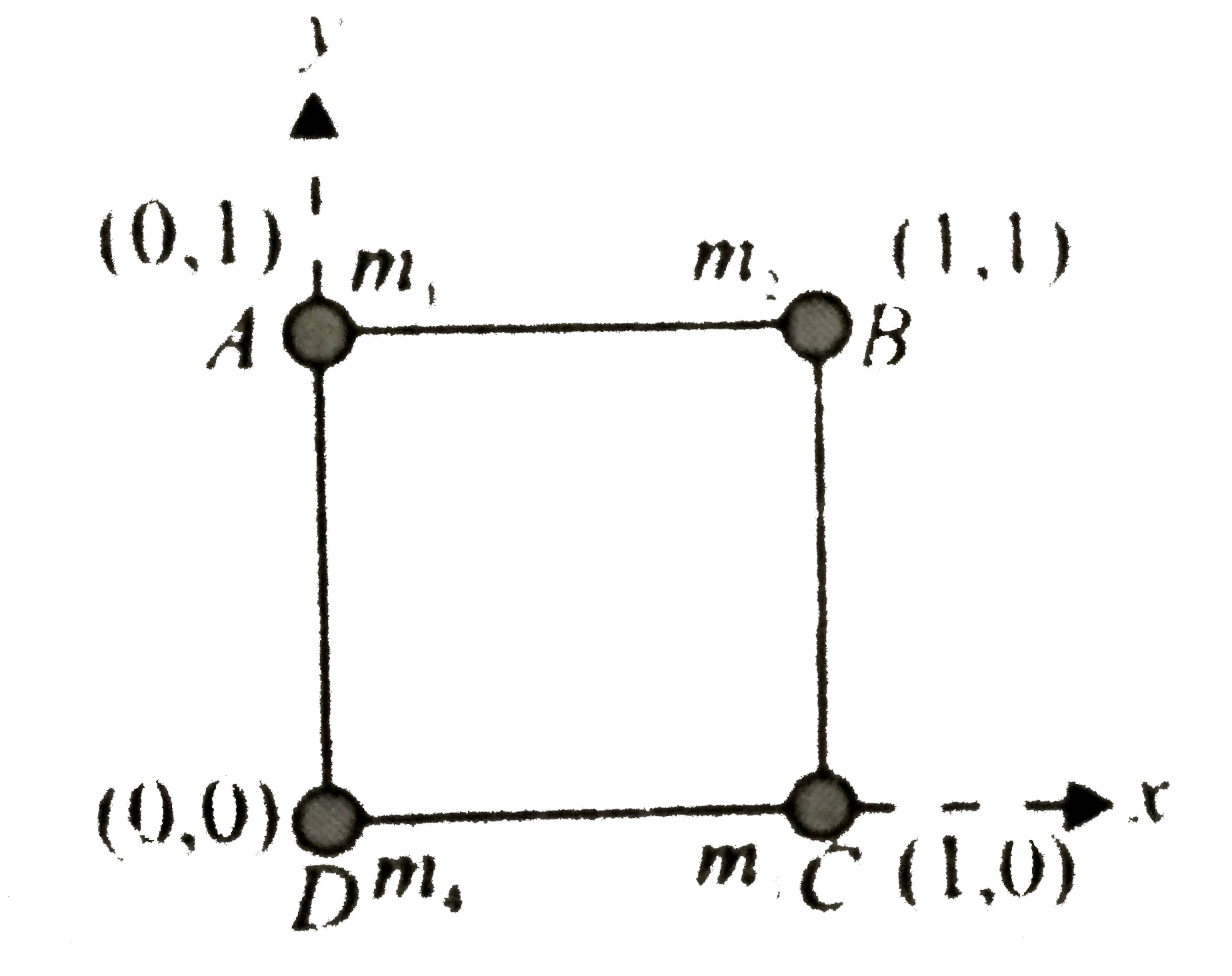 View Solution
View SolutionABCD is parallelogram. If the coordinates of A,B,C are (−2,−1),(3,0) and (1,−2) respectively, find the coordinates of D.
View SolutionABCD is parallelogram. If the coordinates of A,B,C are (−2,−1),(3,0) and (1,−2) respectively, find the coordinates of D.
View SolutionABCD is a parallelogram. If the coordinates of A, B, C are (2,3), (1,4)and (0,−2) respectively, find the coordinates of D.
View Solution

