The magnetic flux through a coil varies with time as ϕ=5t2+6t+9 The ratio of emf at t = 3 s to t = 0 s will be
1:9
1:6
6:1
9:1
The correct Answer is:3
To solve the problem, we need to find the ratio of the electromotive force (emf) at two different times, t=3 seconds and t=0 seconds, given the magnetic flux ϕ(t)=5t2+6t+9.
1. Understand the relationship between emf and magnetic flux:
The induced emf (ε) in the coil is given by Faraday's law of electromagnetic induction:
ε=−dϕdt
Here, ϕ is the magnetic flux.
2. Differentiate the magnetic flux with respect to time:
Given ϕ(t)=5t2+6t+9, we differentiate this with respect to t:
dϕdt=ddt(5t2+6t+9)
Using the power rule of differentiation:
dϕdt=10t+6
3. Calculate the emf at t=3 seconds:
Substitute t=3 into the expression for emf:
ε(3)=10(3)+6=30+6=36V
4. Calculate the emf at t=0 seconds:
Substitute t=0 into the expression for emf:
ε(0)=10(0)+6=0+6=6V
5. Find the ratio of emf at t=3 seconds to t=0 seconds:
The ratio of the emf at t=3 seconds to the emf at t=0 seconds is:
Ratio=ε(3)ε(0)=366=6
6. Express the ratio in standard form:
The ratio can be expressed as:
Ratio=6:1
Final Answer:
The ratio of emf at t=3 seconds to t=0 seconds is 6:1.
The induced emf (ε) in the coil is given by Faraday's law of electromagnetic induction:
ε=−dϕdt
Here, ϕ is the magnetic flux.
Given ϕ(t)=5t2+6t+9, we differentiate this with respect to t:
dϕdt=ddt(5t2+6t+9)
Using the power rule of differentiation:
dϕdt=10t+6
Substitute t=3 into the expression for emf:
ε(3)=10(3)+6=30+6=36V
Substitute t=0 into the expression for emf:
ε(0)=10(0)+6=0+6=6V
The ratio of the emf at t=3 seconds to the emf at t=0 seconds is:
Ratio=ε(3)ε(0)=366=6
The ratio can be expressed as:
Ratio=6:1
The ratio of emf at t=3 seconds to t=0 seconds is 6:1.
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTION & ALTERNATING CURRENTBOOK - VMC MODULES ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTION & ALTERNATING CURRENTEXERCISE - PRACTICE EXERCISE 1
10 Videos
- ELECTROMAGNETIC INDUCTION & ALTERNATING CURRENTBOOK - VMC MODULES ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTION & ALTERNATING CURRENTEXERCISE - PRACTICE EXERCISE 2
10 Videos
- ELECTROMAGNETIC INDUCTION & ALTERNATING CURRENTBOOK - VMC MODULES ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTION & ALTERNATING CURRENTEXERCISE - IN-CHAPTER EXERCISE-G
10 Videos
- DYNAMICS OF A PARTICLEBOOK - VMC MODULES ENGLISHCHAPTER - DYNAMICS OF A PARTICLEEXERCISE - JEE Advance (Archive) Level - II (SINGLE OPTION CORRECT TYPE )
31 Videos
- ELECTROMAGNETIC INDUCTION & ALTERNATIVE CURRENT BOOK - VMC MODULES ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTION & ALTERNATIVE CURRENT EXERCISE - IMPECCABLE
52 Videos
Similar Questions
The magnetic flux through a coil varies with time as ϕ=5t2−6t+9. The ratio of E.M.F. at t=0s to t=0.5s will be
View SolutionThe magnetic flux through a coil varies with timet as shown in the diagram. Which graph best represents the variation of the e.m.f. E induced in the coil with time t?
View SolutionMagnetic flux passing through a coil varies with time as, ϕ=(2t2−4) weber, Resistance of the coil is 10Ω.
View SolutionCurrent (i) passing through a coil varies with time t as i=2t2. At 1 s total flux passing through the coil is 10 Wb. Then
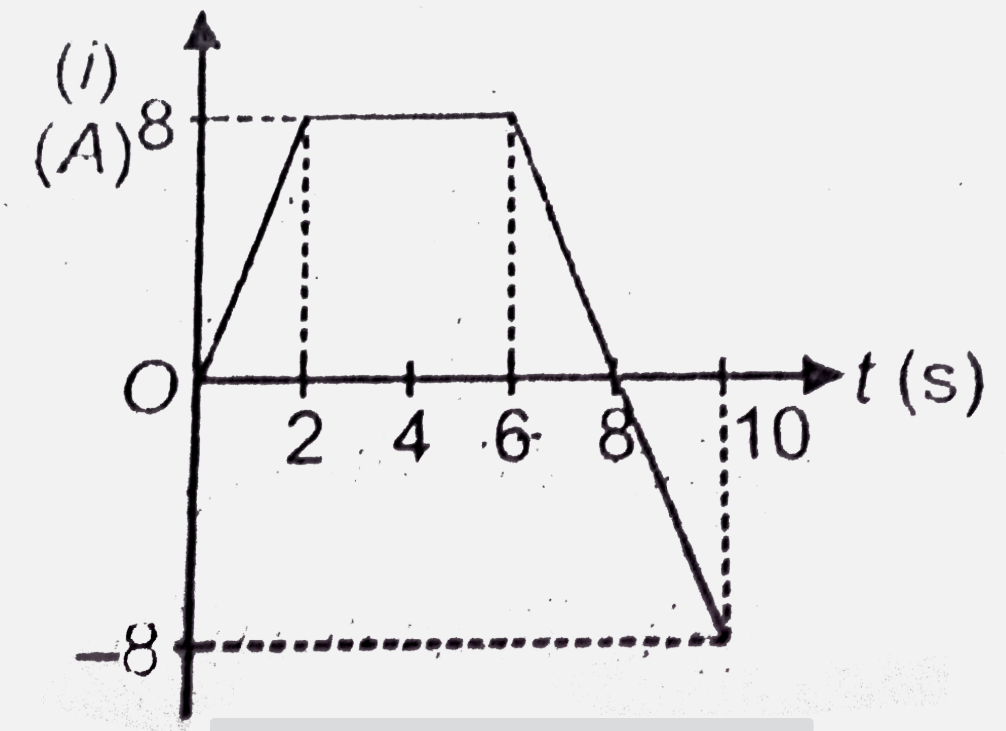
View SolutionThe current I through a conductor varies with time t as shown in figure. The average electric current during t=0 to t=10 s will be
View SolutionA time varying magnetic flux passing through a coil is given by ϕ=xt2, if at t=3s, the emf induced is 9 V, then the value of x is
View SolutionThe magnetic flux passing through a metal ring varies with time t as: ϕB=3(at3−bt2)T−m2 with a=2.00s−3 and b=6.00s−2. The resistance of the ring is 3.0Ω. Determine the maximum current induced in the ring during te interval from t=0 to t=2.0s.
View SolutionA coil of resistance 400Ω is placed in a magnetic field. If the magnetic flux ϕ (wb) linked with the coil varies with time t (sec) as f=50t2+4, the current in the coil at t=2 sec is
View SolutionA coil of resistance 400Ω is placed in a magnetic field. If the magnetic flux ϕ (wb) linked with the coil varies with time t (sec) as f=50t2+4, the current in the coil at t=2 sec is
View SolutionThe magnetic flux linked with a coil (in Wb) is given by the equation ϕ=5t2+3t+16 . The magnetic of induced emf in the coil at fourth second will be
View Solution
