The magnetic flux through a coil varies with time as ϕ=5t2−6t+9. The ratio of E.M.F. at t=0s to t=0.5s will be
(a)9:1
(b)1:6
(c)6:1
(d)1:9
The correct Answer is:C
To solve the problem, we need to find the ratio of the electromotive force (E.M.F.) at two different times, t=0 seconds and t=0.5 seconds, given the magnetic flux ϕ(t)=5t2−6t+9.
1. Identify the formula for E.M.F.:
According to Faraday's law of electromagnetic induction, the E.M.F. (ε) induced in a coil is given by the negative rate of change of magnetic flux:
ϵ=−dϕdt
2. Differentiate the flux function:
We need to differentiate the given flux function ϕ(t)=5t2−6t+9 with respect to time t:
dϕdt=ddt(5t2−6t+9)=10t−6
3. Calculate E.M.F. at t=0 seconds:
Substitute t=0 into the differentiated equation:
ϵ(0)=−dϕdt∣∣∣t=0=−(10(0)−6)=−(−6)=6V
4. Calculate E.M.F. at t=0.5 seconds:
Substitute t=0.5 into the differentiated equation:
ϵ(0.5)=−dϕdt∣∣∣t=0.5=−(10(0.5)−6)=−(5−6)=−(−1)=1V
5. Calculate the ratio of E.M.F.s:
Now, we find the ratio of E.M.F. at t=0 seconds to that at t=0.5 seconds:
Ratio=ϵ(0)ϵ(0.5)=61=6
Final Answer:
The ratio of E.M.F. at t=0 seconds to t=0.5 seconds is 6.
According to Faraday's law of electromagnetic induction, the E.M.F. (ε) induced in a coil is given by the negative rate of change of magnetic flux:
ϵ=−dϕdt
We need to differentiate the given flux function ϕ(t)=5t2−6t+9 with respect to time t:
dϕdt=ddt(5t2−6t+9)=10t−6
Substitute t=0 into the differentiated equation:
ϵ(0)=−dϕdt∣∣∣t=0=−(10(0)−6)=−(−6)=6V
Substitute t=0.5 into the differentiated equation:
ϵ(0.5)=−dϕdt∣∣∣t=0.5=−(10(0.5)−6)=−(5−6)=−(−1)=1V
Now, we find the ratio of E.M.F. at t=0 seconds to that at t=0.5 seconds:
Ratio=ϵ(0)ϵ(0.5)=61=6
The ratio of E.M.F. at t=0 seconds to t=0.5 seconds is 6.
Similar Questions
The magnetic flux through a coil varies with time as ϕ=5t2+6t+9 The ratio of emf at t = 3 s to t = 0 s will be
View SolutionMagnetic flux passing through a coil varies with time as, ϕ=(2t2−4) weber, Resistance of the coil is 10Ω.
View SolutionThe magnetic flux through a coil varies with timet as shown in the diagram. Which graph best represents the variation of the e.m.f. E induced in the coil with time t?
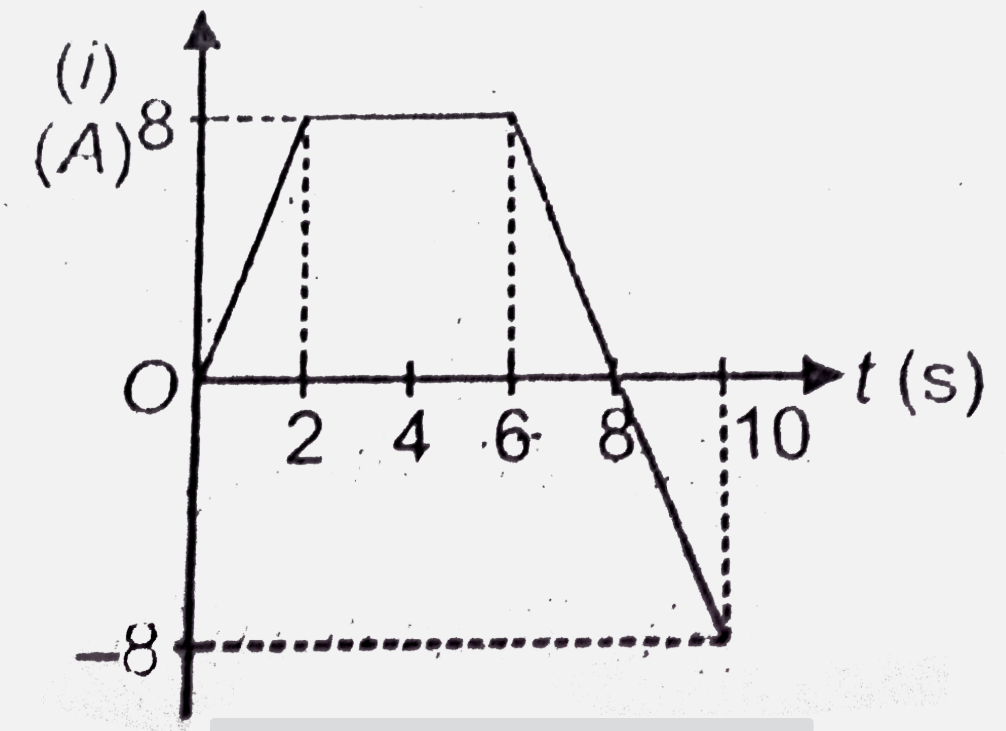
View SolutionThe current I through a conductor varies with time t as shown in figure. The average electric current during t=0 to t=10 s will be
View SolutionThe magnetic flux passing through a metal ring varies with time t as: ϕB=3(at3−bt2)T−m2 with a=2.00s−3 and b=6.00s−2. The resistance of the ring is 3.0Ω. Determine the maximum current induced in the ring during te interval from t=0 to t=2.0s.
View SolutionA coil of resistance 400Ω is placed in a magnetic field. If the magnetic flux ϕ (wb) linked with the coil varies with time t (sec) as f=50t2+4, the current in the coil at t=2 sec is
View SolutionA coil of resistance 400Ω is placed in a magnetic field. If the magnetic flux ϕ (wb) linked with the coil varies with time t (sec) as f=50t2+4, the current in the coil at t=2 sec is
View SolutionCurrent (i) passing through a coil varies with time t as i=2t2. At 1 s total flux passing through the coil is 10 Wb. Then
View SolutionMagnetic flux (in Wb) linked with a closed loop varies with time (in S) as Φ =2t^2+1. The magnitude of induced emf at t=1 s is
View SolutionMagnetic flux (in Wb) linked with a closed loop varies with time (in S) as Φ =2t^2+1. The magnitude of induced emf at t=1 s is
View Solution
