Question

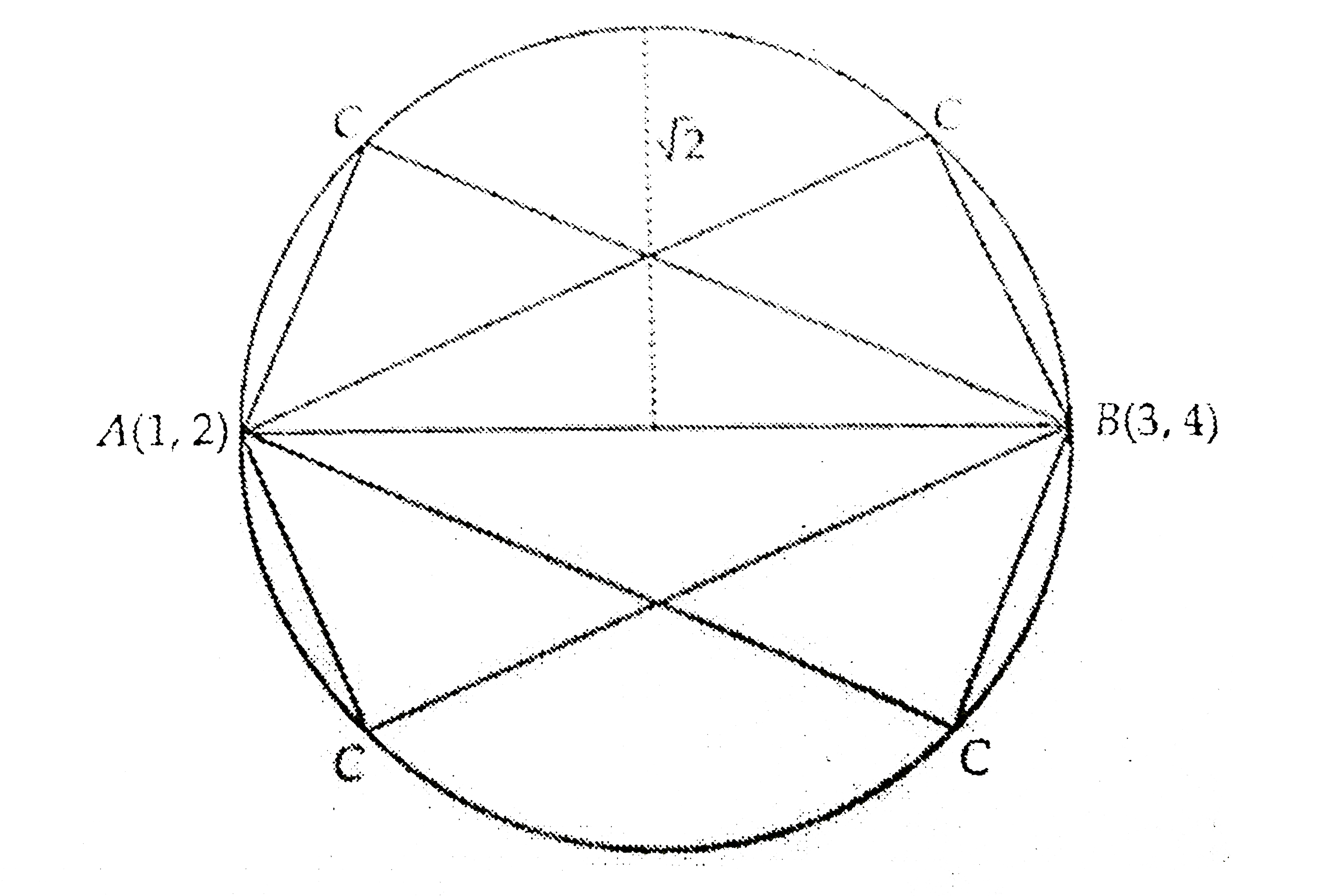
Let $A(1,2),B(3,4)$ be two points and $C(x,y)$ be a point such that area of $\Delta ABC$ is 3 sq. units and $(x-1)(x-3)+(y-2)(y-4)=0$. Then number of positions of C, in the xy plane is

Options

A. 2
B. 4
C. 8
D. none of these

Explanation

We have ,
(x - 1) (x-3) + (y-2) (y-4) = 0
`implies` Point C (x,y) lies on the circle with AB as a diameter .
Now ,
Area of `Delta`ABC = 1 sq. unit
`implies (1)/(2) (AB) xx` (Altitude) = 1
`implies (1)/(2) xx 2sqrt2 xx` Altitude = 1 `implies` Altitude = `(1)/(sqrt2) lt` Radius
Thus , there are four possible positions of C as shown in Fig. 35 .