X is a random variable with distribution given below
x:0123P(X=x):k3k3kk
The value of k and its variance are
The correct Answer is:18,32,34
To solve the problem, we need to find the value of k and the variance of the random variable X with the given probability distribution.
The distribution is given as:
- P(X=0)=k
- P(X=1)=3k
- P(X=2)=3k
- P(X=3)=k
Step 1: Find the value of k
We know that the sum of all probabilities must equal 1:
P(X=0)+P(X=1)+P(X=2)+P(X=3)=1
Substituting the probabilities, we have:
k+3k+3k+k=1
This simplifies to:
8k=1
Now, solving for k:
k=18
Step 2: Write the probabilities with the value of k
Now that we have k, we can express the probabilities:
- P(X=0)=k=18
- P(X=1)=3k=38
- P(X=2)=3k=38
- P(X=3)=k=18
Step 3: Calculate the mean μ
The mean μ of the random variable X is calculated as:
μ=E(X)=∑(xi⋅P(X=xi))
Calculating this:
μ=0⋅18+1⋅38+2⋅38+3⋅18
μ=0+38+68+38=128=32
Step 4: Calculate E(X2)
Next, we need to calculate E(X2):
E(X2)=∑(x2i⋅P(X=xi))
Calculating this:
E(X2)=02⋅18+12⋅38+22⋅38+32⋅18
E(X2)=0+38+128+98=248=3
Step 5: Calculate the variance σ2
The variance σ2 is given by:
σ2=E(X2)−(E(X))2
Substituting the values we calculated:
σ2=3−(32)2
σ2=3−94
To subtract, we convert 3 to a fraction:
σ2=124−94=34
Final Answers
Thus, the value of k is 18 and the variance is 34.
---
- P(X=0)=k
- P(X=1)=3k
- P(X=2)=3k
- P(X=3)=k
P(X=0)+P(X=1)+P(X=2)+P(X=3)=1
Substituting the probabilities, we have:
k+3k+3k+k=1
This simplifies to:
8k=1
Now, solving for k:
k=18
- P(X=0)=k=18
- P(X=1)=3k=38
- P(X=2)=3k=38
- P(X=3)=k=18
μ=E(X)=∑(xi⋅P(X=xi))
Calculating this:
μ=0⋅18+1⋅38+2⋅38+3⋅18
μ=0+38+68+38=128=32
E(X2)=∑(x2i⋅P(X=xi))
Calculating this:
E(X2)=02⋅18+12⋅38+22⋅38+32⋅18
E(X2)=0+38+128+98=248=3
σ2=E(X2)−(E(X))2
Substituting the values we calculated:
σ2=3−(32)2
σ2=3−94
To subtract, we convert 3 to a fraction:
σ2=124−94=34
Similar Questions
A random variable X has the following distribution
X=x1:1234P(X=x1):k2k3k4k
The value of k and P(X<3) are equal to
View SolutionA random variable X has the following distribution
x:1234P(X=x):k23k25k27k2
The value of k is
View SolutionA random variable X has the following distribution
X=x1:−2−10123P(X=x1):0.1k0.22k0.3k
The value of k and its mean and variance are
View SolutionIf the probability of a random variable X is a given below :
X=x:−2−10123P(X=x):110k152k310k
Then the value of k, is :
View SolutionIf X is a random variable with probability distribution as given below: X=xi: 0 1 2 3 P(X=xi):k 3k 3k k The value of k and its variance are (A) 18,2227 (B) 18,2327 (C) 18,2427 (D) 18,34
View SolutionThe probability distribution of a random variable X is given by.
X=x:01234P(X=x):0.40.30.10.10.1
The variance of X, is
View SolutionA discrete random variable X has the probability distribution given below: X:0.511.52 P(X):kk22k2k Find the value of k. (ii) Determine the mean of the distribution.
View SolutionThe probability distribution of a random variable is given below:
X=x01234567P(X=x)0k2k2k3kk22k27k2+k
Then P(0<X<5)=
View SolutionIf mandσ2 are the mean and variance of the random variable X, whose distribution is given by:
X=x:0123P(X=x):1312016
View SolutionA discrete random variable X has the probability distribution as given below
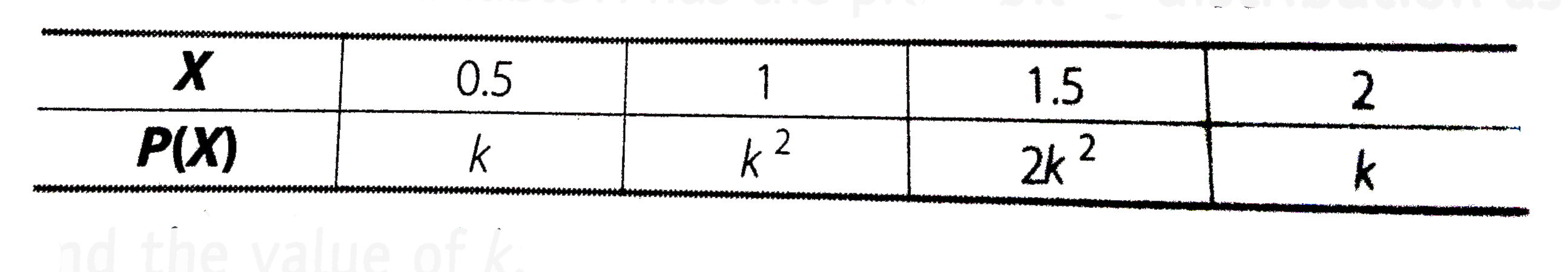
(i) Find the value of k.
(ii) Determine the mean of the distribution.
View Solution
