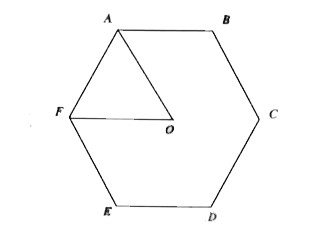
If ABCDEF is regular hexagon, then AD+EB+FC is

A

$2 A \to B$

B

$\to 0$

C

$3 A \to B$

D

$4 A \to B$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:D

Let $A \to B = \to a and B \to C = \to b .$ Then ,
$A \to O = B \to C = \to b, O \to C = F \to O = \to a$

In $Δ A O B$ , we have
$A \to B + B \to O = A \to O$
$\Rightarrow \to a + B \to O = \to b [∵ A \to O = B \to C = \to b]$
$\Rightarrow B \to O = \to b - \to a$
$\Rightarrow B \to E = 2 B \to O = 2 (\to b - \to a)$
$∴ A \to D + E \to B + F \to C = A \to D - B \to E + 2 O \to C$
$\Rightarrow A \to D + E \to B + F \to C = 2 \to b - 2 (\to b - \to a) + 2 \to a = 4 \to a = 4 A \to B$

Updated on:21/07/2023

|

Class 12 MATHS VECTOR ALGEBRA

Topper's Solved these Questions

Similar Questions

Knowledge Check

In the figure shown, ABCDEF is a regular hexagon and AOF is an equilateral triangle. The perimeter of $Δ A O F$ is 2a feet. What is the perimeter of the hexagon in feet?

A2a
B3a
C4a
D6a

OBJECTIVE RD SHARMA ENGLISH-ALGEBRA OF VECTORS-Chapter Test

Home
Ask Doubt
Profile