Let L1 be a straight line passing through (0,0)andL2 be x+y=1. If the intercepts made by the circel x2+y2−x+3y=0onL1andL2 are equal, then which of the following equations can represent L1?
x+y=0,x−7y=0
x−y=0,x+7y=0
7x+y=0
x−7y=0
The correct Answer is:B
The centre and radius of the given circle are (12,−32) and √52 respectively.
Let y=mx be the equation of L1. Then,
p1= Length of the intercept on L1
⇒p1=2
⎷(√52)2−(m+32√m2+1)2=2
⎷52−(m+3)24(m2+1)
and,
⇒p2= Length of the intercept on L2
⇒p2=2√(√52)2−(√2)2=2√52−2=√2
Now,
p1=p2
⇒2
⎷52−(m+3)24(m2+1)=√2
⇒5−(m+3)24(m2+1)=1
⇒7m2−6m−1=0
⇒(m−1)(7m+1)=0⇒m=1,−17
So, the equations of L1 are y=x and 7y=−x.
Topper's Solved these Questions
- BOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - CIRCLESEXERCISE - Section I - Solved Mcqs108videos
CIRCLES
- BOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - CIRCLESEXERCISE - Section-I (Solved MCQs)1videos
CIRCLES
- BOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - CARTESIAN PRODUCT OF SETS AND RELATIONS EXERCISE - Chapter Test30videos
CARTESIAN PRODUCT OF SETS AND RELATIONS
- BOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - COMPLEX NUMBERS EXERCISE - Chapter Test58videos
COMPLEX NUMBERS
Similar Questions
Let L1 be a straight line passing through the origin and L2 be the straight line x+y=1 if the intercepts made by the circle x2+y2−x+3y=0 on L1 and L2 are equal, then which of the following equations can represent L1?
View SolutionLet l be the line through (0,0) an tangent to the curve y=x3+x+16. Then the slope of l equal to :
View SolutionA line L is perpendicular to the line 3x−4y−7=0 and touches the circle x2+y2−2x−4y−4=0, the y-intercept of the line L can be:
View SolutionA line L is perpendicular to the line 3x−4y−7=0 and touches the circle x2+y2−2x−4y−4=0, the y-intercept of the line L can be:
View SolutionConsider the lines given by
L1:x+3y−5=0
L2:3x−ky−1=0
L3:5x+2y−12=0
Match the following lists.
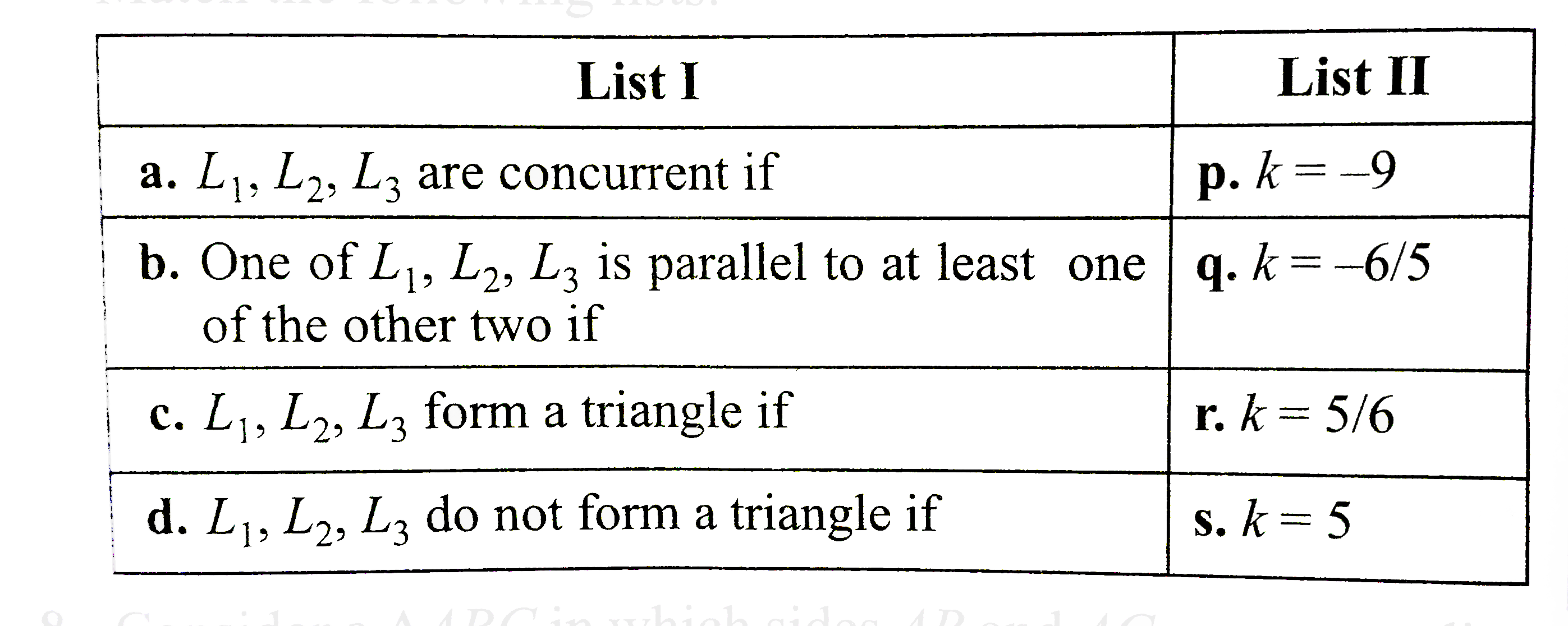 View Solution
View SolutionA straight line L through the point (3,-2) is inclined at an angle 60∘ to the line √3x+y=1. If L also intersects the x-axis then find the equation of L .
View Solutiont1,t2,t3 are lengths of tangents drawn from a point (h,k) to the circles x2+y2=4,x2+y2−4=0andx2+y2−4y=0 respectively further, t41=t22 t23+16. Locus of the point (h,k) consist of a straight line L1 and a circle C1 passing through origin. A circle C2 , which is equal to circle C1 is drawn touching the line L1 and the circle C1 externally.
Equation of L1 isView SolutionThe combined equation of the lines L1 and L2 is 2x2+6xy+y2=0 and that lines L3 and L4 is 4x2+18xy+y2=0. If the angle between L1 and L4 be α, then the angle between L2 and L3 will be
View SolutionIf the line lx+my−1=0 touches the circle x2+y2=a2 , then prove that (l,m) lies on a circle.
View SolutionIf the line lx+my−1=0 touches the circle x2+y2=a2 , then prove that (l,m) lies on a circle.
View Solution

