The maximum value of $∣ ∣ ∣ a r g (\frac{1}{1 - z}) ∣ ∣ ∣ f or | z | = 1, z \neq 1$ is given by.

A

$\frac{π}{6}$

B

$\frac{π}{3}$

C

$\frac{π}{2}$

D

$π$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:C

Let $ω = \frac{1}{1 - z}$ . Then, $z = 1 - \frac{1}{ω}$
$∴ | z | - 1 \Rightarrow ∣ ∣ ∣ 1 - \frac{1}{ω} ∣ ∣ ∣ - 1 \Rightarrow | ω - 1 | - | ω |$

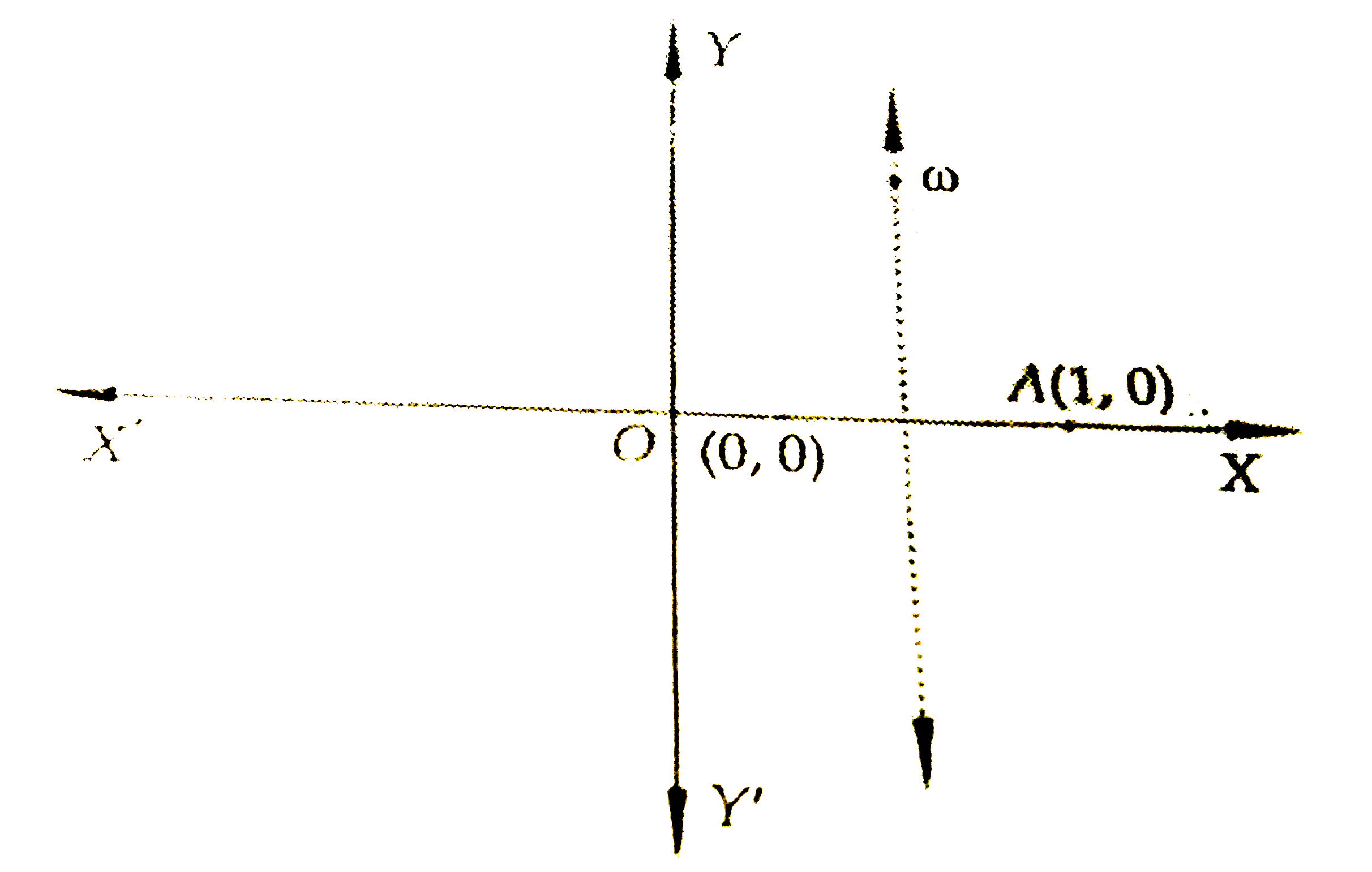
Thus, the locus of $ω$ is perpendicular bisector of the line segment joining (0,0) and (1,0)
Hence, arg $(ω) \to \frac{π}{2}$ as $z \to 1$ .

Updated on:21/07/2023

|

Class 12 MATHS COMPLEX NUMBERS

Topper's Solved these Questions

Similar Questions

OBJECTIVE RD SHARMA ENGLISH-COMPLEX NUMBERS -Section I - Solved Mcqs

Home
Ask Doubt
Profile