If |z1|=|z2| and arg (z1)+arg(z2)=0, then
7√72√3
5√72√3
14√7√3
7√75√3
The correct Answer is:B
We have,
∣∣√3(1−2z)+2i∣∣=2√7
∣∣√3(1−2z)+2i∣∣=2√7
⇒∣∣−2√3z+(√3+2i)∣∣=2√7
⇒∣∣
∣∣z−(12+1√3i)∣∣
∣∣=√73
Clearly, it represents a circle haivng center at (1/2,1/√3) and radius r1=√73. it is given that z1 lies on (i)
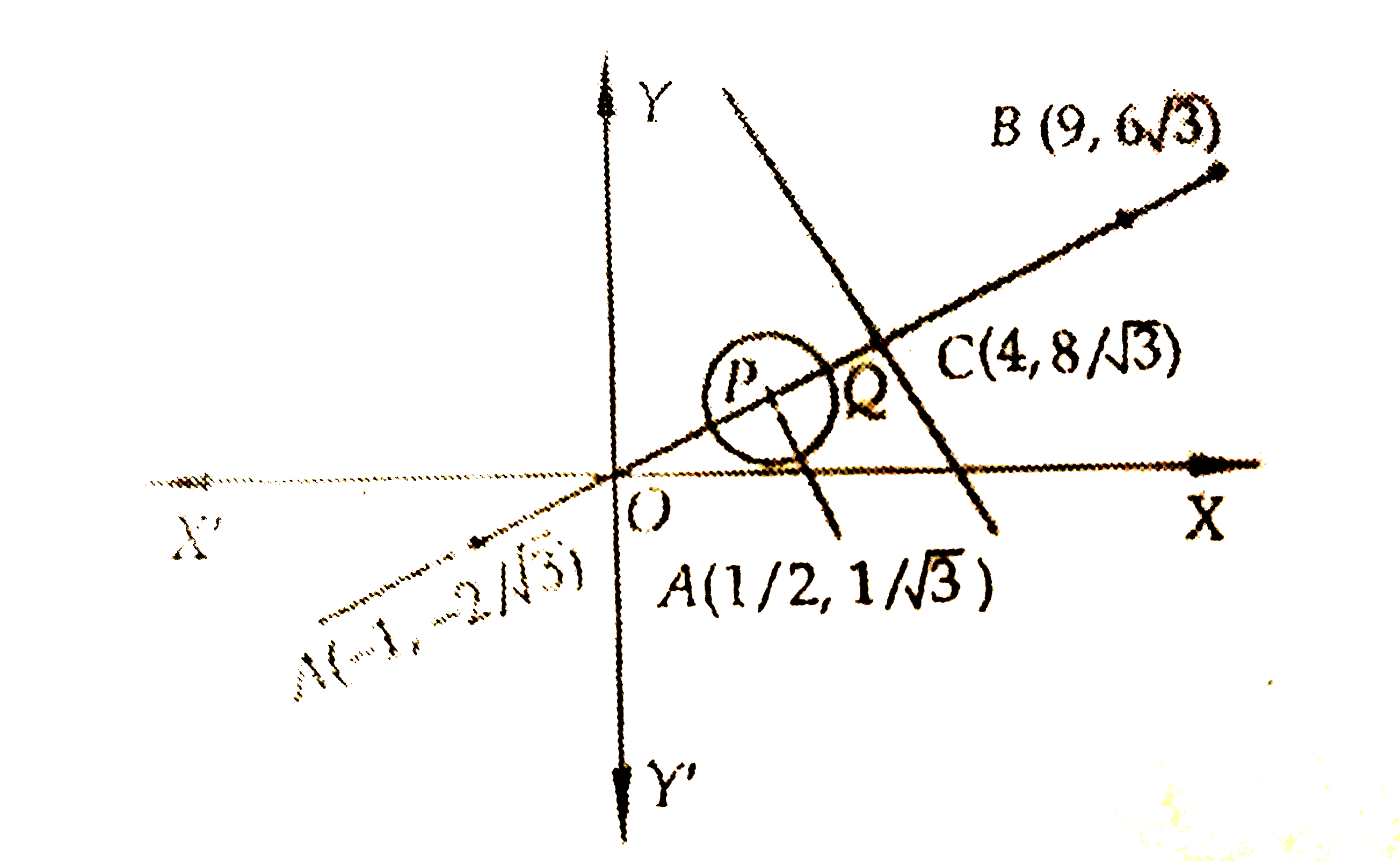
The equation of another curve is
∣∣√3(−1−z)−2i∣∣=∣∣√3(9−z)+18i∣∣
or ∣∣∣−1−z−2√3i∣∣∣=∣∣9−z+6√3i∣∣
or ,∣∣∣z+1+2√3i∣∣∣=∣∣z−9−6√3i∣∣
or ,∣∣
∣∣z−(−1−2√3i)∣∣
∣∣=∣∣z−(9+6√3i)∣∣
This, represents perpendicular bisector of the line segement joining point A(−1,−2√3) and B(9,6√3). The coordinates of the mid-point C of AB are (4,8/√3). Clearly, A,B and the center of the circle are collinear.
Topper's Solved these Questions
- BOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - COMPLEX NUMBERS EXERCISE - Section II - Assertion Reason Type15videos
COMPLEX NUMBERS
- BOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - COMPLEX NUMBERS EXERCISE - Exercise129videos
COMPLEX NUMBERS
- BOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - COMPLEX NUMBERS EXERCISE - Chapter Test58videos
COMPLEX NUMBERS
- BOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - CIRCLESEXERCISE - Chapter Test53videos
CIRCLES
- BOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - CONTINUITY AND DIFFERENTIABILITYEXERCISE - Exercise87videos
CONTINUITY AND DIFFERENTIABILITY
Similar Questions
If |z1|=|z2| and arg (z1/z2)=π, then
find the of z1z2.View Solutionz1thez2are two complex numbers such that|z1|=|z2|. "and"
arg (z1)+arg(z2=π, then show that z1=−¯z2.View SolutionIf z1, z2 are complex numbers such that Re(z1)=|z1−2|, Re(z2)=|z2−2| and arg(z1−z2)=π/3 , then Im(z1+z2)=
View SolutionIf |z1|=|z2| and arg(z1z2)=π, then z1+z2 is equal to (a) 0 (b) purely imaginary (c) purely real (d) none of these
View SolutionIf z1 and z2 are to complex numbers such that two |z1|=|z2|+|z1−z2|, then arg (z1)−arg(z2)
View SolutionIf z1andz2 are two complex numbers such that |z1|=|z2|andarg(z1)+arg(z2)=π , then show that z1,=−(z)2.
View SolutionIf the complex number Z1 and Z2,arg(Z1)−arg(Z2)=0. then show that |z1−z2|=|z1|−|z2|.
View SolutionIf the complex number Z1 and Z2,arg(Z1)−arg(Z2)=0. then show that |z1−z2|=|z1−z2|.
View SolutionStatement-1 : let z1andz2 be two complex numbers such that arg (z1)=π3andarg(z2)=π6 then arg (z1z2)=π2
and
Statement -2 : arg(z1z2)=arg(z1)+arg(z2)+2kπ,k∈{0,1,−1}View SolutionState true or false for the following.
Let z1 and z2 be two complex numbers such that |z2+z2|=|z1|+|z2| , then arg (z1−z2)=0View Solution

