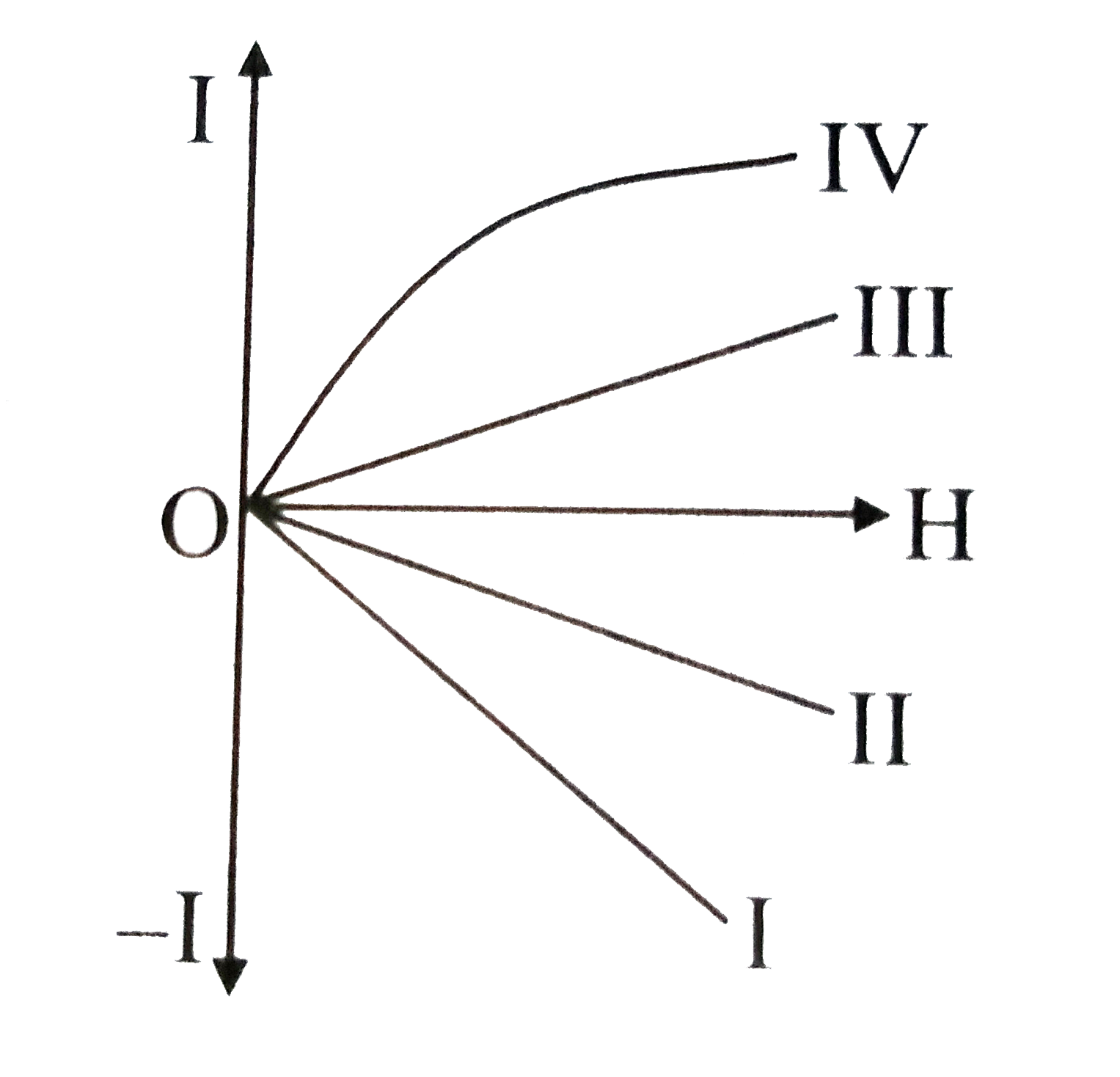
The most appropriate I-H curve for a paramagnetic substances is
(a) OA
(b) OB
(c) OC
(d) OD

:χm (susceptiblitity) =IH
for paramagnet substances , 0<χm<E, where E is a small positive number .
Hence I vs H graph is a staight line with small positive slop or OC.
Topper's Solved these Questions
- MAGNETIC EFFECTS OF CURRENT AND MAGNETISMBOOK - MTG GUIDECHAPTER - MAGNETIC EFFECTS OF CURRENT AND MAGNETISMEXERCISE - NEET CAFE (TOPICWISE PRACTICE QUESTIONS)(BIOT SAVART LAW AND ITS APPLICATIONS)
47 Videos
- MAGNETIC EFFECTS OF CURRENT AND MAGNETISMBOOK - MTG GUIDECHAPTER - MAGNETIC EFFECTS OF CURRENT AND MAGNETISMEXERCISE - NEET CAFE (TOPICWISE PRACTICE QUESTIONS)(AMPER.S CIRCUITAL LAW AND ITS APPLICATIONS)
8 Videos
- ELECTROSTATICSBOOK - MTG GUIDECHAPTER - ELECTROSTATICSEXERCISE - AIPMT/NEET (MCQ.s)
34 Videos
- OPTICSBOOK - MTG GUIDECHAPTER - OPTICSEXERCISE - AIPMT/NEET
55 Videos
Similar Questions
Knowledge Check
The most appropriate magnetization M versus magnetising field H curve for a paramagnetic substance is
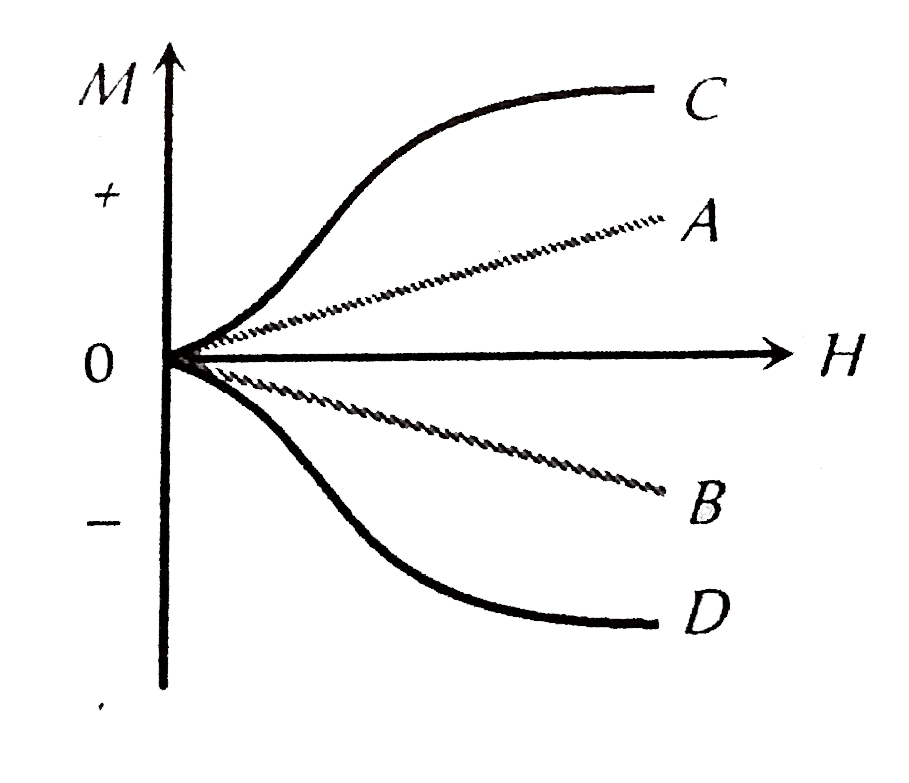 AABBCCDD
AABBCCDDLet ABCD be a parallelogram whose diagonals intersect at P and let O be the origin. What is −−→OA+−−→OB+−−→OC+−−→OD equal to
A2−−→OPB4−−→OPC6−−→OPD8−−→OPIn the given figure, rays OA, OB, OC and OD are such that ∠AOB = 50∘ , ∠BOC = 90∘, ∠COD=70∘ and ∠AOD=x∘. Then, the value of x is
 A50∘B70∘C150∘D90∘
A50∘B70∘C150∘D90∘
The following figure shows a trapezium ABCD in which AB is parallel to DC and AD= BC
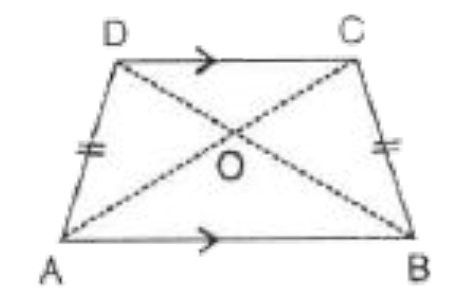
Prove that:
OA = OB and OC= OD
View SolutionOABCD is a pyramid with square base ABCD such that ¯¯¯¯¯¯OA,¯¯¯¯¯¯OB,¯¯¯¯¯¯OC,¯¯¯¯¯¯OD are unit vectors and ¯¯¯¯¯¯OA,¯¯¯¯¯¯OB=¯¯¯¯¯¯OB.¯¯¯¯¯¯OC=¯¯¯¯¯¯OC.¯¯¯¯¯¯OD=¯¯¯¯¯¯OD.¯¯¯¯¯¯OA=12, then volume of the pyramid is
View SolutionTwo fixed point AandB are taken on the two axes such that OA=a,OB=b, two variable points C,D are taken on the same axes respectively, find the locus of the point of intersection of ADandCB if : 1OC−1OD=1OA−1OB
View SolutionIf ABCD is a rombus whose diagonals cut at the origin O, then OA + OB + OC + OD equals to
View SolutionIf diagonals of a parallelogram ABCD intersect each other in M, then ¯¯¯¯¯¯OA+¯¯¯¯¯¯OB+¯¯¯¯¯¯OC+¯¯¯¯¯¯OD =
View Solution