L and M are the mid-points of sides AB and DC respectively of parallelogram ABCD. Prove that segments DL and BM trisect diagonal AC.
ABCD is a parallelogram
∴ AB=DCandAB||DC
⇒ 2AE=2CFandAE||CF
⇒ AE=CFandAE||CF
⇒□AECF is a parallelogram
∴ AF||EC

In ΔDCM,
F is the mid-point of DC
and FN||CM
∴ N is the mid-point of DM.
⇒ DN=MN ...(1)
In ΔBAN,
E is the mid-point of AB.
and EM||AN
∴ M is the mid-point of BN.
⇒ BM=MN ...(2)
From eqs, (1) and (2)
BM=MN=ND
⇒ AF and CE, divides the diagonal BD into three equal parts.
Topper's Solved these Questions
- BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - QUADRILATERALSEXERCISE - Problems From NCERT/exemplar11videos
QUADRILATERALS
- BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - QUADRILATERALSEXERCISE - Exercise 8a29videos
QUADRILATERALS
- BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - PROBABILITYEXERCISE - Revision Exercise (very Short Answer /short Answer Questions)10videos
PROBABILITY
- BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - STATISTICSEXERCISE - Revision Exercise12videos
STATISTICS
Similar Questions
In a parallelogram ABCD, E and F are the mid-points of sides BC and AD respectively. Show that the line segment BF and ED trisect the diagonal AC.
View SolutionIn a parallelogram ABCD, E and F are the mid-points of sides AB and CD respectively. Show that the line segments AF and EC trisect the diagonal BD.
 View Solution
View SolutionIf P and Q are the mid points of the sides AB and CD of a parallelogram ABCD, prove that DP and BQ cut the trisection which also the points of trisection of DP and BQ respectively.
View SolutionIn Figure, ABCD is a parallelogram. E and F are the mid-points of the sides AB and CD respectively. Prove that the line segments AF and CE trisect (divide into three equal parts) the diagonal BD .
View SolutionIn Figure, ABCD is a parallelogram. E and F are the mid-points of the sides AB and CD respectively. Prove that the line segments AF and CE triset (divide into three equal parts) the diagonal BD.
View SolutionX and Y are the mid-points of the opposite sides AB and DC of a parallelogram ABCD. Prove that □AXCY is a parallelogram.
View SolutionD, E and F are the mid-points of the sides BC, CA and AB respectively of triangle ABC. Prove that:
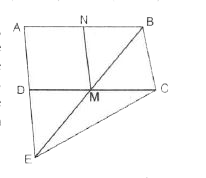
BDEF is a parallelogram.View SolutionIn the given figure, M and N are the mid-points of the sides DC and AB respectively of the parallelogram ABCD.
If the area of parallelogram ABCD is 48cm2,
(i) State the area of the triangle BEC.
(ii) name the parallelofram which is equal in area to the triangle BEC.
 View Solution
View SolutionIn the diagram below, P and Q are midpoints of sides BC and AD respectively of the parallelogram ABCD. If side AB = diagonal BD: prove that the quadrilateral BPDQ is a rectangle.
 View Solution
View SolutionDL and BM are the height on sides AB and AD respectively of parallelogram ABCD. If the area of the parallelogram is 1470 cm2,AB=35 cmandAD=49 cm find the BM and DL.
View Solution

