If the mid -point of the consecvitve sides of any quadrilateral are connected by staight line segments, prove that the resulting quadrilteral is a parallelogram .
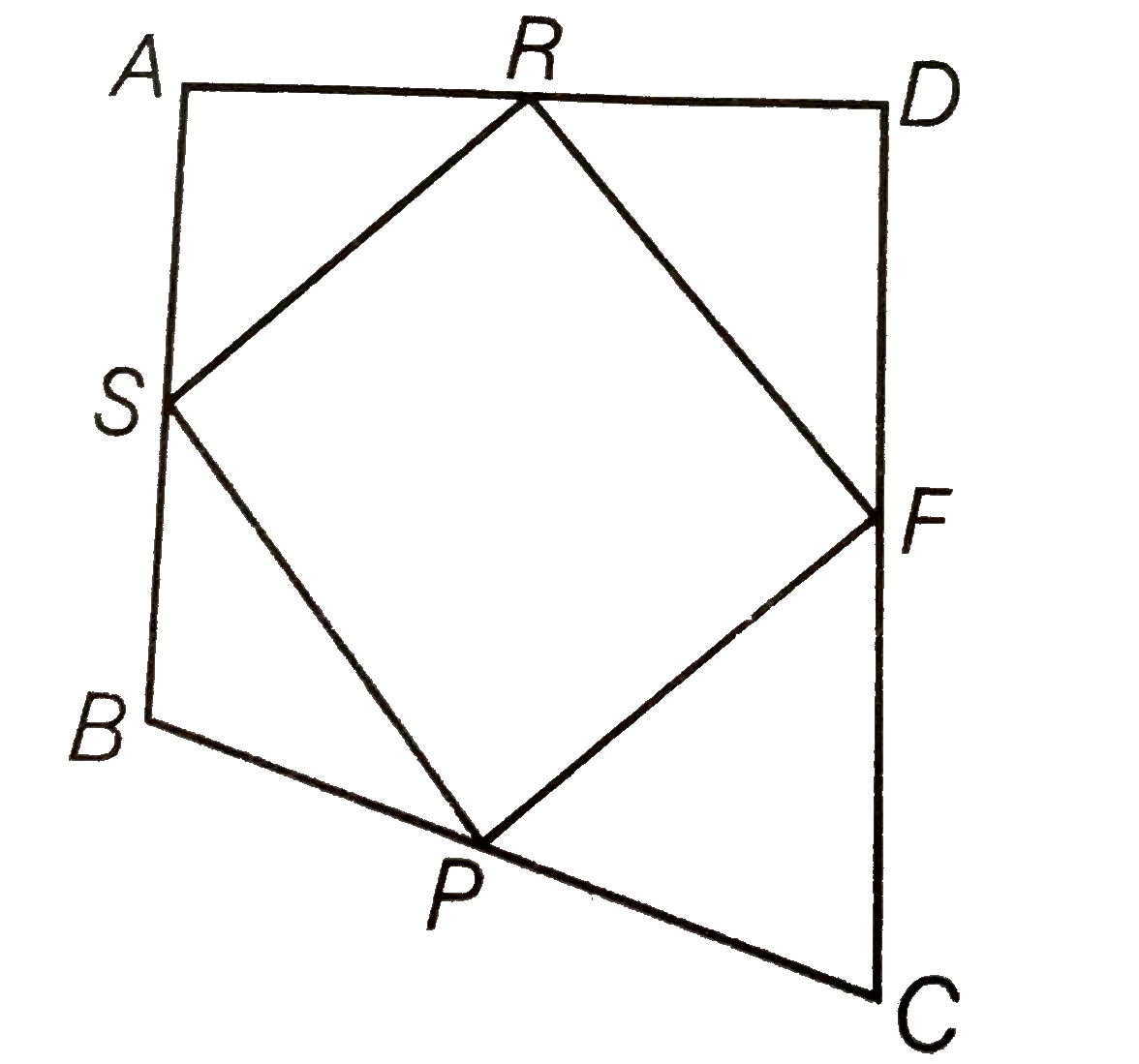
Given :□ABCD in which P,Q,R and S are respectively the mid-points AB, BC ,CD and DA.
To prove :□PQRS is a parallelogram.
Construction: Join AC.
Proof: In △ABC, since P and Q are the mid-points of AB and BC respectively.
∴PQ||ACandPQ=12AC (mid-point theorem)...(1)
Now, in △ADS, since S and R are the mid-point of AD and DC respectively.
∴SR∣∣ACandSR=12AC (mid-point theorem)...(2)
∴ From eqs. (1) and (2) , we get
PQ||SRandPQ=SR
Thus, in quadrilateral PQRS, one pair of opposite sides is parallel and equal.
Hence, □PQRS is a parallelogram. Hence proved.
Topper's Solved these Questions
- BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - QUADRILATERALSEXERCISE - Problems From NCERT/exemplar11videos
QUADRILATERALS
- BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - QUADRILATERALSEXERCISE - Exercise 8a29videos
QUADRILATERALS
- BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - PROBABILITYEXERCISE - Revision Exercise (very Short Answer /short Answer Questions)10videos
PROBABILITY
- BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - STATISTICSEXERCISE - Revision Exercise12videos
STATISTICS
Similar Questions
If the mid points of consecutive of a quadrilateral connected by straight lines prove that the resulting quadrilateral is a parallelogram.
View SolutionIf the mid-points of the sides of a quadrilateral are joined in order, prove that the area of the parallelogram, so formed will be half of the area of the given quadrilateral (figure).
 View Solution
View SolutionProve that the quadrilateral formed by joining the mid-points of the pairs of consecutive sides of a quadrilateral is a parallelogram.
View SolutionWhich of the following statements are true (T) and which are false (F)? (i) In a parallelogram, the diagonals are equal. (ii) In a parallelogram, the diagonals bisect each other. (iii) In a parallelogram, the diagonals intersect each other at right angles. (iv) In any quadrilateral, if a pair of opposite sides is equal, it is a parallelogram. (v) If all the angles of a quadrilateral are equal, it is a parallelogram. (vi) If three sides of a quadrilateral are equal , it is a parallelogram. (vii) If three angles of a quadrilateral are equal, it is a parallelogram. (viii) If all the sides of a quadrilateral are equal it is a parallelogram
View SolutionShow that the line segments joining the mid-points of the opposite sides of a quadrilateral bisect each other
View SolutionShow that the line segments joining the mid-points of the opposite sides of a quadrilateral bisect each other.
View SolutionShow that the line segments joining the mid-points of the opposite sides of a quadrilateral bisect each other
View SolutionProve that the line segments joints joining the mid-points of the adjacent sides of a quadrilateral from a parallelogram.
View SolutionProve that the figure formed by joining the mid-points of the pair of consecutive sides of a quadrilateral is a parallelogram. OR ABCD is a parallelogram in which P,Q,R and S are mid-points of the sides AB,BC,CD and DA respectively. AC is a diagonal. Show that : PQ∣∣AC and PQ=12AC SR∣∣AC and SR=12AC PQ=SR (iv) PQRS is a parallelogram.
View SolutionShow that the line segments joining the mid-points of opposite sides of a quadrilateral bisects each other.
View Solution

