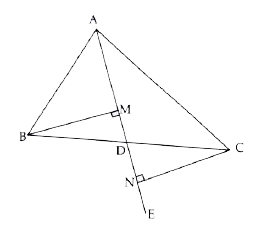
In the adjoining figure, D is the mid-point of BC. If BM and CN are perpendiculars from B and C respectively on AD and AD produced, then prove that BM = CN.

Given : ΔABC in which D is the mid-point of BC, BM⊥AD and CN⊥AD
To Prove : BM=CN
Proof : In ΔBMD and ΔCND,
∵⎧⎪⎨⎪⎩∠BMD=∠CND(each 90∘, given)∠BDM=∠CDN(vertically opposite angle)BD=CD(given)
∵ΔBMD≅ΔCND (AAS)
⇒BM=CN (c.p.c.t) Hence Proverd.
Topper's Solved these Questions
- BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - TRIANGLESEXERCISE - Problems From NCERT/exemplar5videos
TRIANGLES
- BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - TRIANGLESEXERCISE - Exercise 7a35videos
TRIANGLES
- BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - SURFACE AREA AND VOLUMEEXERCISE - Revision Exercise (long Answer Questions)10videos
SURFACE AREA AND VOLUME
Similar Questions
In Figure, AD is a median and BL,CM are perpendiculars drawn from B and C respectively on AD and AD produced. Prove that BL=CM. Figure
View SolutionIn Figure, AD is a median and BL, CM are perpendiculars drawn from B and C respectively on AD and AD produced. Prove that BL=CM
View SolutionIn the given figure ABC is a triangle and D is the mid-point of BC. AD is produced to E. BM and CN are two perpendiculars dropped from B and C respectively on AE.
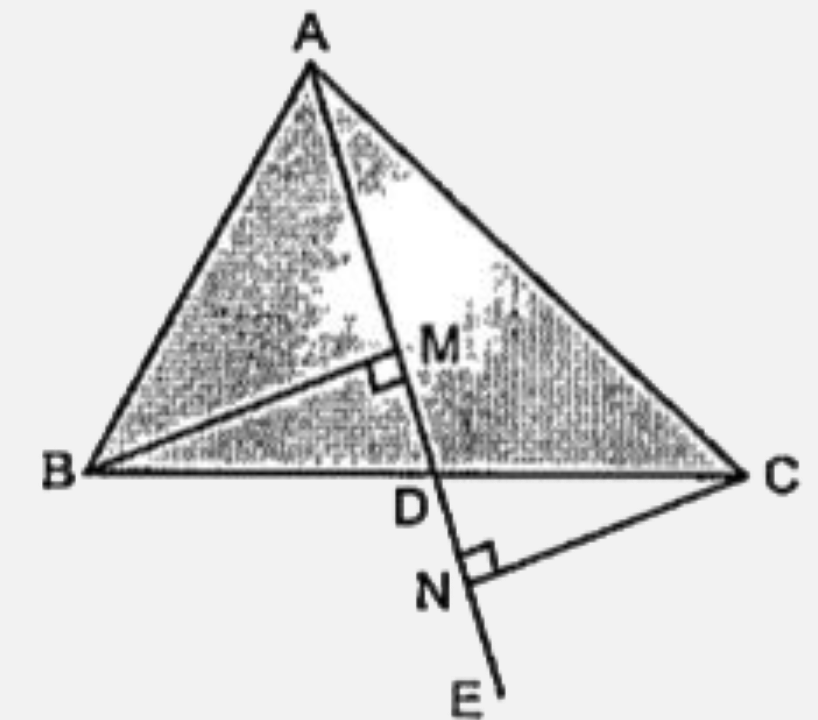
Prove that :
BM=CNView SolutionIn the adjoining figure, BM and DN are the perpendiculars from B and D respectively to AC such that BM = DN. Prove that BO = OD.
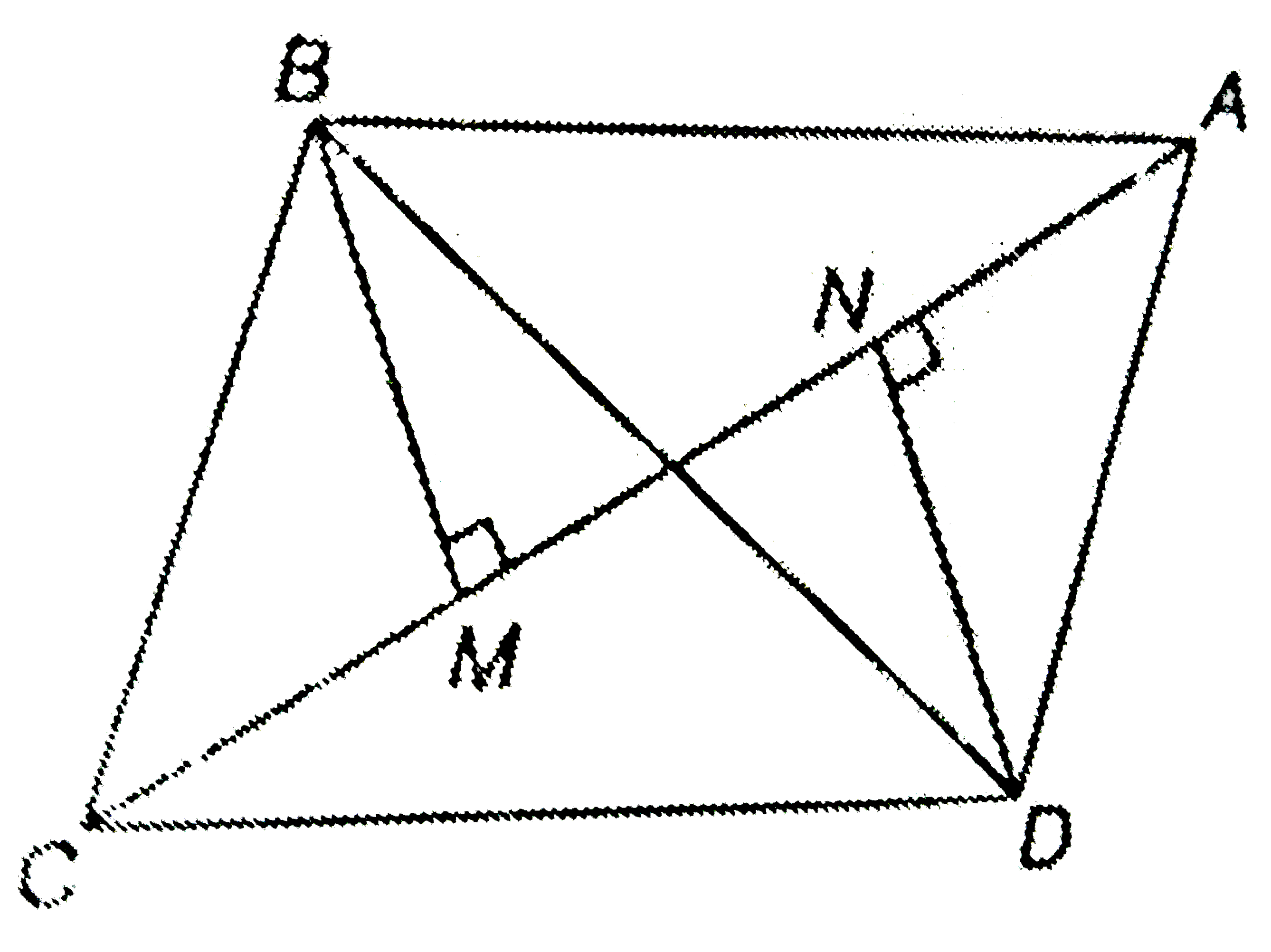 View Solution
View SolutionIn the given figure ABC is a triangle and D is the mid-point of BC. AD is produced to E. BM and CN are two perpendiculars dropped from B and C respectively on AE.

Prove that :
ΔBMD≅ΔCNDView SolutionIn the given figure ABC is a triangle and D is the mid-point of BC. AD is produced to E. BM and CN are two perpendiculars dropped from B and C respectively on AE.
Prove that : (i) ΔBMD≅ΔCND (ii) BM = CN
 View Solution
View SolutionIf D id the mid-point of the side BC of a triangle ABC and AD is perpendicular to AC , then
View SolutionABC is a triangle and D is the mid-point of BC . The perpendiculars from D to AB and AC are equal. Prove that the triangle is isosceles.
View SolutionABC is a triangle and D is the mid-point of BC . The perpendiculars from D to AB and AC are equal. Prove that the triangle is isosceles.
View SolutionABC is a triangle. D is the middle point of BC. If AD is perpendicular to AC, The value of cos A cos C , is
View Solution

