ABCD is a trapezium in which AB||DC and P,Q are points on AD and BC respectively, such that PQ||DC, if PD=18 cm, BQ=35 cm and QC=15 cm. Find AD.
To solve the problem step by step, we will use the properties of trapeziums and the basic proportionality theorem.
Step 1: Understand the problem
We have a trapezium ABCD where AB is parallel to DC. Points P and Q are on sides AD and BC respectively, and PQ is also parallel to DC. We know the lengths PD, BQ, and QC.
Step 2: Draw the trapezium
Draw trapezium ABCD with AB parallel to DC. Mark points P on AD and Q on BC such that PQ is parallel to DC.
Step 3: Label the known lengths
- PD = 18 cm
- BQ = 35 cm
- QC = 15 cm
Step 4: Apply the Basic Proportionality Theorem
Since PQ is parallel to DC, we can apply the Basic Proportionality Theorem (also known as Thales' theorem). This theorem states that if a line is drawn parallel to one side of a triangle, it divides the other two sides proportionally.
In triangle ABD:
APPD=ABPQ
Let AP=x. Then, we can express the equation as:
x18=ABPQ
In triangle BDC:
BQQC=BDPQ
Substituting the known values:
3515=BDPQ
Step 5: Set up the equations
From the two triangles, we can equate the ratios:
APPD=BQQC
Substituting the known values:
x18=3515
Step 6: Solve for AP
Cross-multiply to solve for x:
15x=18×35
Calculating the right side:
15x=630
Now divide by 15:
x=63015=42 cm
Step 7: Find AD
Now that we have AP:
AD=AP+PD=42 cm+18 cm=60 cm
Final Answer
The length of AD is 60 cm.
---
We have a trapezium ABCD where AB is parallel to DC. Points P and Q are on sides AD and BC respectively, and PQ is also parallel to DC. We know the lengths PD, BQ, and QC.
Draw trapezium ABCD with AB parallel to DC. Mark points P on AD and Q on BC such that PQ is parallel to DC.
- PD = 18 cm
- BQ = 35 cm
- QC = 15 cm
Since PQ is parallel to DC, we can apply the Basic Proportionality Theorem (also known as Thales' theorem). This theorem states that if a line is drawn parallel to one side of a triangle, it divides the other two sides proportionally.
APPD=ABPQ
Let AP=x. Then, we can express the equation as:
x18=ABPQ
BQQC=BDPQ
Substituting the known values:
3515=BDPQ
From the two triangles, we can equate the ratios:
APPD=BQQC
Substituting the known values:
x18=3515
Cross-multiply to solve for x:
15x=18×35
Calculating the right side:
15x=630
Now divide by 15:
x=63015=42 cm
Now that we have AP:
AD=AP+PD=42 cm+18 cm=60 cm
The length of AD is 60 cm.
Topper's Solved these Questions
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - TRIANGLESEXERCISE - Long Answer Type Questions18videos
TRIANGLES
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - TRIANGLESEXERCISE - Very Short Answer Typw Questions12videos
TRIANGLES
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - SURFACE AREAS AND VOLUMESEXERCISE - LONG ANSWER TYPE QUESTIONS20videos
SURFACE AREAS AND VOLUMES
Similar Questions
ABCD is a rectangle measuring 60 cm by 50 cm P,Q,and R are the points on AB, AD , and BC, respectively, such that AP=40cm,AQ=20cm,andBR=40cm. Find the area of the polygon QPBCD.
View SolutionIf P and Q are points on the sides AB and AC respeactively of △ABC, if PQ||BC,l AP= 2 cm , AB = 6 cm and AC= 9 cm find AQ.
View SolutionABCD is a square. P, Q and Rare the points on AB, BC and CD respectively, such that AP = BQ = CR. Prove that:
PB = QCView SolutionABCD is a square. P, Q and Rare the points on AB, BC and CD respectively, such that AP = BQ = CR. Prove that:
PQ = QRView SolutionP and Q are points on the sides AB and AC respectively of a △ABC. If AP= 2cm, PB = 4cm AQ= 3cm and QC= 6cm. Show that BC= 3PQ.
View SolutionABCD is a trapezium with AB || DC. E and F are points on non-parallel sides AD and BC respectively such that EF is parallel to AB. Show thatAEED=BFFC.
View SolutionThe figure, given below, shows a trapezium ABCD. M and N are the mid-points of the nonparallel sides AD and BC respectively. Find:
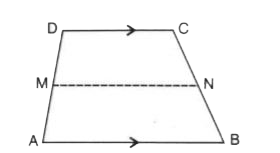
DC, if MN = 15 cm and AB = 23 cm.View SolutionIn ΔABC,D and E are the points on sides AB and AC respectively.
Find whether DE || BC, if :
AB = 9 cm, AD = 4 cm, AE = 6 cm and EC = 7.5 cm.View SolutionIn ΔABC, D and E are points on the sides AB and AC respectively. Find whether DE//BC, if :
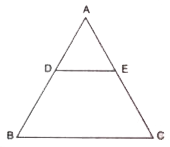
AD=7cm, BD=45cm,AE=35cm and CE=56cmView SolutionABCD is a trapezium in which AB∣∣DCand∠A=∠B=45∘. Find angles C and D of the trapezium.
View Solution

