Show that the trajectory of an object thrown at certain angle with the horizontal is a parabola.

Text Solution

Verified by Experts

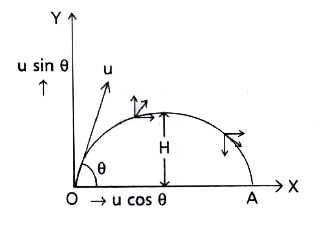
Consider a body is projected with an initial velocity (u) making an angle $θ$ with the horizontal. The body does not experience acceleration in horizontal direction. The velocity of the projectile can be resolved in to (i) $u cos θ$ , horizontal component (ii) $u sin θ$ , vertical component. The horizontal component of velocity remains constant through out the motion. Only its vertical component changes due to acceleration due to gravity (g).
The distance travelled along OX in time t is given by $x = u cos θ \times t$
$t = \frac{x}{u cos θ}$ .....(1)
The distance travelled along on in time t is given by
$y = (u cos θ) t \frac{1}{2} g t^{2}$ .............(2) $⎡ ⎢ ⎣ \begin{matrix} (∵ u = u sin θ) a = - g s = y \end{matrix} ⎤ ⎥ ⎦$
$y = (u sin θ) \frac{x}{u cos θ} - \frac{1}{2} g (\frac{x^{2}}{u^{2} {cos}^{2} θ})$
$y = x tan θ - (\frac{g}{2 u^{2} {cos}^{2} θ}) x^{2}$
Let $A = tan θ$ and $B = \frac{g}{2 u^{2} {cos}^{2} θ}$
$Y = A x - B x^{2}$ where A and B are constants.
This is equaiton of parabola.
$∴$ The trajectory of a projectile is parabola.

Updated on:21/07/2023

The trajectory of an object is determined by
AIts location
BIts velocity at various moments
CBoth (1) and (2)
DNone of the above
The trajectory of a projectile fired horizontally with velocity u is parabola given by-
A $y = \frac{g}{2 u^{2}} x^{2}$
B $y = - \frac{g}{2 u^{2}} x^{2}$
C $y = \frac{g}{2 u^{2}} y^{2}$
D $y = \frac{g}{2 u^{2}} y^{2}$
The angle which the velocity vector of a projectile thrown with a velocity v at an. angle $θ$ to the horizontal Will make with the horizontal after time t of its being thrown up is
A $θ$
B ${tan}^{- 1} (θ / t)$
C ${tan}^{- 1} (\frac{v cos θ}{v sin θ - g t})$
D ${tan}^{- 1} (\frac{v sin θ - g t}{v cos θ})$