A simple pendulum with a bob of mass m and a conducting wire of length L, swings under gravity with an angular amplitude 2θ. If the horizontal component of the earth's magnetic field perpendicular to the plane of motion of the pendulum is B, then the maximum emf induced across the pendulum is
2BLsin(θ2)(gL)1/2
BLsin(θ2)(2gL)1/2
2BLsin(θ2)(gL)3/2
BLsin(θ2)(gL)2
The correct Answer is:A
To find the maximum emf induced across the pendulum, we can follow these steps:
Step 1: Understand the setup
We have a simple pendulum with a bob of mass m and a length L. The pendulum swings with an angular amplitude of 2θ. The horizontal component of the Earth's magnetic field, which is perpendicular to the plane of motion of the pendulum, is B.
Step 2: Determine the maximum velocity of the pendulum bob
The maximum height h that the bob reaches can be determined using the formula:
h=L(1−cosθ)
Using the conservation of energy, the potential energy at the maximum height is equal to the kinetic energy at the lowest point:
mgh=12mv2
Substituting for h:
mgL(1−cosθ)=12mv2
Cancelling m from both sides:
gL(1−cosθ)=12v2
Thus, we can express v2 as:
v2=2gL(1−cosθ)
Step 3: Relate 1−cosθ to sin2
Using the trigonometric identity 1−cosθ=2sin2(θ/2):
v2=2gL(2sin2(θ/2))=4gLsin2(θ/2)
Step 4: Calculate the maximum emf induced
The emf (E) induced in the pendulum can be expressed as:
E=B⋅L⋅v
Substituting v=√4gLsin2(θ/2)=2√gLsin(θ/2):
E=B⋅L⋅(2√gLsin(θ/2))
Thus, the maximum emf induced across the pendulum is:
Emax=2BL√gLsin(θ/2)
Final Answer
The maximum emf induced across the pendulum is:
Emax=2BL√gLsin(θ/2)
---
We have a simple pendulum with a bob of mass m and a length L. The pendulum swings with an angular amplitude of 2θ. The horizontal component of the Earth's magnetic field, which is perpendicular to the plane of motion of the pendulum, is B.
The maximum height h that the bob reaches can be determined using the formula:
h=L(1−cosθ)
Using the conservation of energy, the potential energy at the maximum height is equal to the kinetic energy at the lowest point:
mgh=12mv2
Substituting for h:
mgL(1−cosθ)=12mv2
Cancelling m from both sides:
gL(1−cosθ)=12v2
Thus, we can express v2 as:
v2=2gL(1−cosθ)
Using the trigonometric identity 1−cosθ=2sin2(θ/2):
v2=2gL(2sin2(θ/2))=4gLsin2(θ/2)
The emf (E) induced in the pendulum can be expressed as:
E=B⋅L⋅v
Substituting v=√4gLsin2(θ/2)=2√gLsin(θ/2):
E=B⋅L⋅(2√gLsin(θ/2))
Thus, the maximum emf induced across the pendulum is:
Emax=2BL√gLsin(θ/2)
The maximum emf induced across the pendulum is:
Emax=2BL√gLsin(θ/2)
Similar Questions
A simple pendulum with bob of mass m and conducting wire of length L swings under gravity through an angle 2θ. The earth's magnetic field component in the direction perpendicular to swing is B. The maximum potential difference induced across the pendulum is
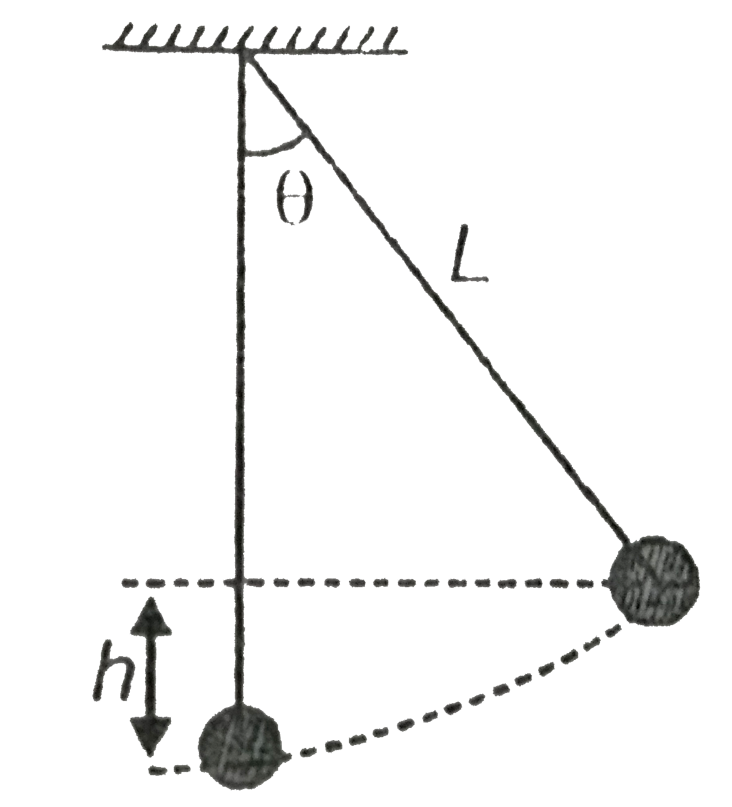
View SolutionA simple pendulum with bob of mass m and conducting wire of length L swings under gravity through an angle 2θ. The earth's magnetic field component in the direction perpendicular to swing is B. The maximum potential difference induced across the pendulum is

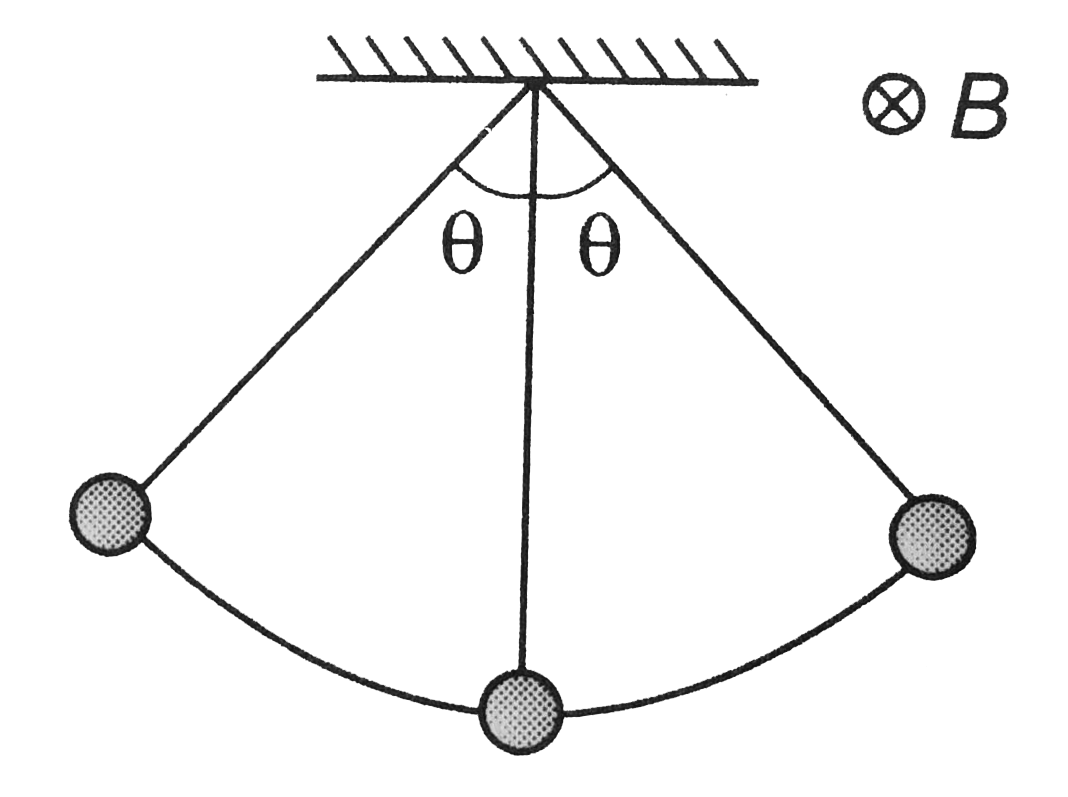
View SolutionA simple pendulum with charge bob is oscillating as shown in the figure. Time period of oscillation is T and angular ampliltude is θ. If a uniform magnetic field perpendicular to the plane of oscillation is switched on, then
View SolutionA simple pendulum with a bob of mass m swings with an angular amplitude of 40∘. When its angular displacement is 20∘, the tension in the string is greater than mgcos20∘
View SolutionA simple pendulum of length 1 m with a bob of mass m swings with an angular amplitude 30∘. Then (g=9.8m/s2
View SolutionA simple pendulum has a bob of mass m and swings with an angular amplitude ϕ. The tension in thread is T. At a certain time the string makes an angle θ with the vertical (θ≤ϕ)
View SolutionA simple pendulum with a bob of mass m swings with an angular amplitude of 40∘. When its angular displacement is 20∘, the tension in the string is greater than mgcos20∘ true
false
View SolutionA vertical rod of length l is moved with constant velocity v towards east. The vertical component of earth magnetic field is B and angle of dip is θ. The induced e.m.f. in the rod is
View SolutionAt a perpendicular place on the earth, the horizontal component of earth's magnetic field of B, and the angle of dip is θ. A striaght meridian and is moved horizontally perpendicular to its length with a velocity v. The emf induced across the rod is
View SolutionA semicircular conducting wire of radius a is moving perpendicular to a uniform magnetic field B with speed√2vas shown in the figure.The emf induced across the wire Is
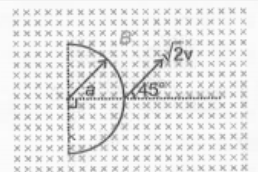
View Solution
