A block of mass 10kg is suspended from string of length 4m. When pulled by a force F along horizontal from midpoint. Upper half of string makes 45∘ with vertical, value of F is
100N
75N
90N
85N
The correct Answer is:A
To solve the problem, we need to analyze the forces acting on the block when it is pulled horizontally, causing the string to make an angle of 45∘ with the vertical.
1. Identify the Forces:
- The weight of the block W=mg acts downward, where m=10kg and g=9.8m/s2.
- The tension T in the string acts along the string at an angle of 45∘ with the vertical.
- The horizontal force F is applied at the midpoint of the string.
2. Calculate the Weight of the Block:
W=mg=10kg×9.8m/s2=98N
3. Resolve the Tension into Components:
- The vertical component of the tension T is given by:
Ty=Tcos(45∘)=T⋅1√2=T√2
- The horizontal component of the tension T is given by:
Tx=Tsin(45∘)=T⋅1√2=T√2
4. Apply the Equilibrium Condition in the Vertical Direction:
Since the block is in equilibrium vertically, the upward tension must balance the weight:
Ty=W⟹T√2=98N
Solving for T:
T=98√2N
5. Apply the Equilibrium Condition in the Horizontal Direction:
The horizontal component of the tension must equal the applied force F:
Tx=F⟹T√2=F
Substituting T from the previous step:
F=98√2√2=98N
Final Answer:
The value of the force F is 98N.
- The weight of the block W=mg acts downward, where m=10kg and g=9.8m/s2.
- The tension T in the string acts along the string at an angle of 45∘ with the vertical.
- The horizontal force F is applied at the midpoint of the string.
W=mg=10kg×9.8m/s2=98N
- The vertical component of the tension T is given by:
Ty=Tcos(45∘)=T⋅1√2=T√2
- The horizontal component of the tension T is given by:
Tx=Tsin(45∘)=T⋅1√2=T√2
Since the block is in equilibrium vertically, the upward tension must balance the weight:
Ty=W⟹T√2=98N
Solving for T:
T=98√2N
The horizontal component of the tension must equal the applied force F:
Tx=F⟹T√2=F
Substituting T from the previous step:
F=98√2√2=98N
The value of the force F is 98N.
Topper's Solved these Questions
Similar Questions
An object of mass 10kg is connected to the lower end of a massless string of length 4m hanging from the ceiling. If a force F is applied horizontally at the mid-point of the string, the top half of the string makes an angle of 45∘ with the vertical , then the magnitude of F is
View SolutionA body of mass √3 kg is suspended by a string to a rigid support. The body is pulled horizontally by a force F until the string makes an angle of 30° with the vertical. The value of F and tension in the string are.
View Solution
Knowledge Check
A block fof mass 5kg is suspended by a massless rope of length 2 m from the ceilling. A force of 50 N is applied in the horizontal direction at the midpoint P of the rope, as shown in the figure. The angle made by the rope with the vertical in equilibrium is (Take g=10ms−2m .
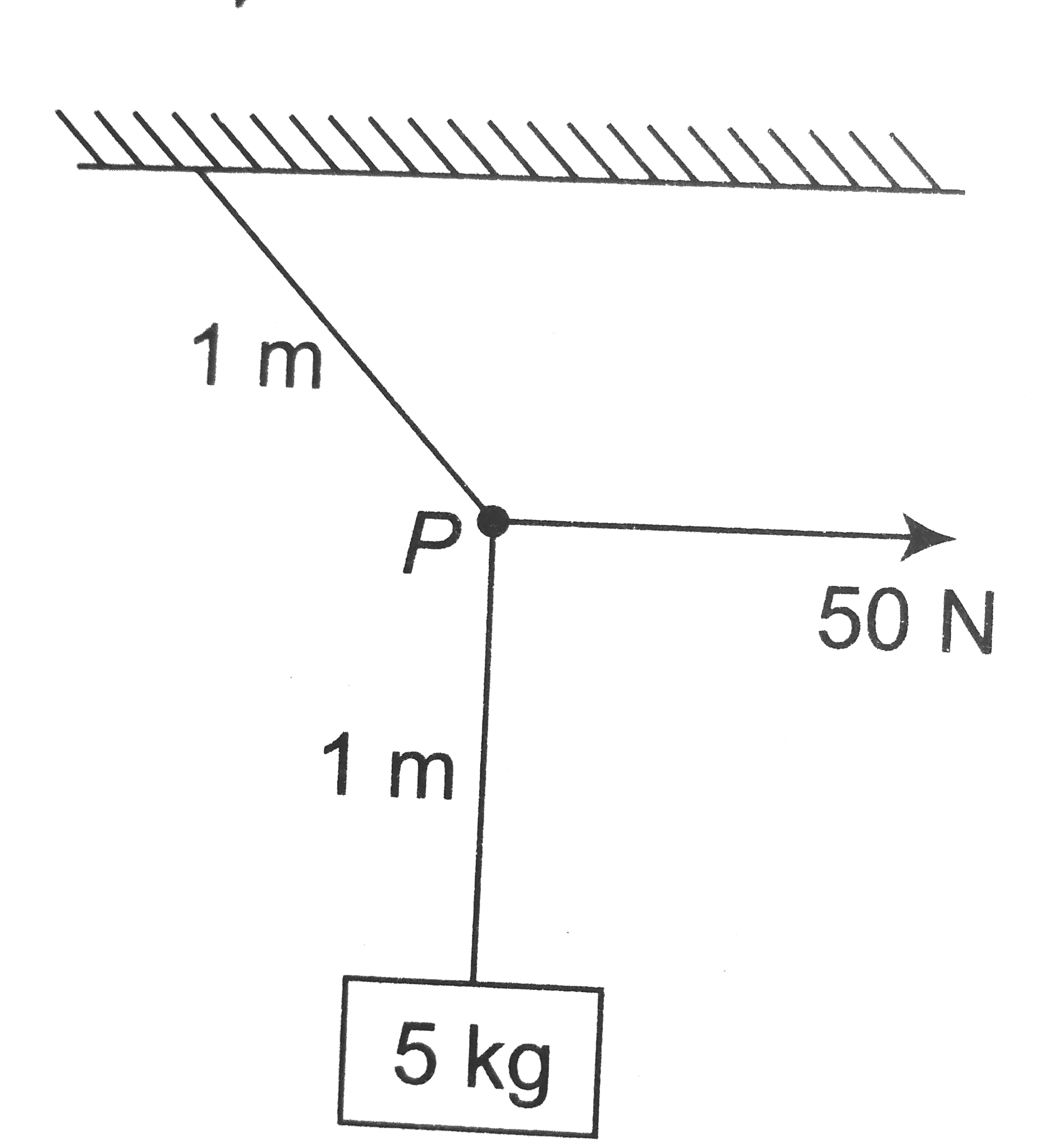 A30∘B40∘C60∘D45∘
A30∘B40∘C60∘D45∘
A mass of 10 kg is suspended from a spring balance. It is pulled aside by a horizontal string so that it makes an angle of 60∘ with the vertical. The new rading of the balance is
View SolutionA bob of mass 1 kg is suspended from an inextensible string of length 1 m. When the string makes an angle 60∘ with vertical, speed of the bob is 4 m/s
Net acceleration of the bob at this instant is
View SolutionA bob of mass 1 kg is suspended from an inextensible string of length 1 m. When the string makes an angle 60∘ with vertical, speed of the bob is 4 m/s
Upto what maximum height will the bob rise with respect to the bottommost point ?
View SolutionA mass of M kg is suspended by a weightless string. The horizontal force required to displace it until string makes an angle of 45∘ with the initial vertical direction is:
View SolutionA body of mass 10 kg is suspended by a string and is pulled a side with a horizontal force of 49 N. Find the tension in the string, if the body is in equilibrium under these forces.
View SolutionAn object of mass m is tied to a string of length l and a variable force F is applied on it which brings the string gradually at angle θ with the vertical. Find the work done by the force F
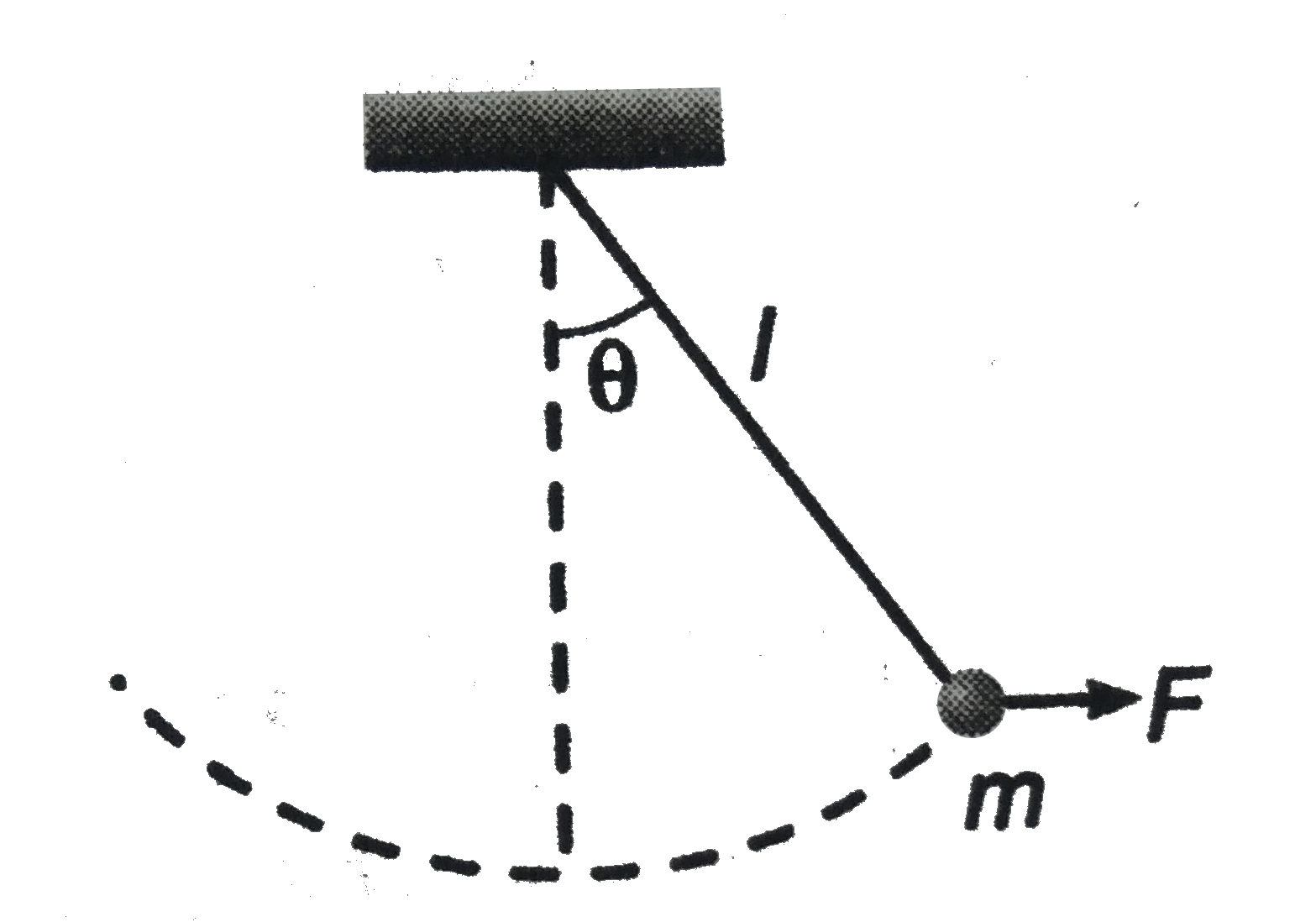 .
.
View SolutionA bullet of mass 0.01kg and travelling at a speed of 500ms−1 strikes a block of mass 2kg which is suspended by a string of length 5m. The centre of gravity of the block is found to raise a vertical distance of 0.2m. What is the speed of the bullet after it emerges from the block?
View Solution
