A particle is executing SHM with time period T. If time period of its total mechanical energy isT' then T'T is
2
12
Zero
Infinite
The correct Answer is:4
To solve the problem, we need to analyze the relationship between the time period of a particle executing Simple Harmonic Motion (SHM) and the time period of its total mechanical energy.
1. Understanding SHM:
- A particle in SHM oscillates back and forth around an equilibrium position. The motion can be described by a sinusoidal function, and it has a specific time period T.
2. Total Mechanical Energy in SHM:
- The total mechanical energy E of a particle in SHM is given by the formula:
E=12mω2A2
where m is the mass of the particle, ω is the angular frequency, and A is the amplitude of the motion.
3. Constant Nature of Total Mechanical Energy:
- In SHM, both m, ω, and A are constants. Therefore, the total mechanical energy E remains constant throughout the motion.
4. Time Period of Total Mechanical Energy:
- Since the total mechanical energy E is constant, it does not oscillate or vary with time. Hence, we can say that the time period of the total mechanical energy T′ is infinite.
5. Finding the Ratio:
- We are asked to find the ratio T′T. Since T′ is infinite and T is a finite value (the time period of the SHM), we have:
T′T=∞T=∞
Conclusion:
The ratio T′T is infinite.
- A particle in SHM oscillates back and forth around an equilibrium position. The motion can be described by a sinusoidal function, and it has a specific time period T.
- The total mechanical energy E of a particle in SHM is given by the formula:
E=12mω2A2
where m is the mass of the particle, ω is the angular frequency, and A is the amplitude of the motion.
- In SHM, both m, ω, and A are constants. Therefore, the total mechanical energy E remains constant throughout the motion.
- Since the total mechanical energy E is constant, it does not oscillate or vary with time. Hence, we can say that the time period of the total mechanical energy T′ is infinite.
- We are asked to find the ratio T′T. Since T′ is infinite and T is a finite value (the time period of the SHM), we have:
T′T=∞T=∞
The ratio T′T is infinite.
Topper's Solved these Questions
- OSCILLATIONSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - OSCILLATIONSEXERCISE - ASSIGNMENT (SECTION-B )
25 Videos
- OSCILLATIONSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - OSCILLATIONSEXERCISE - ASSIGNMENT ( SECTION-C )
11 Videos
- OSCILLATIONSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - OSCILLATIONSEXERCISE - Try Yourself
86 Videos
- NUCLEIBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - NUCLEIEXERCISE - ASSIGNMENT (SECTION-D)
10 Videos
- PHYSICAL WORLDBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - PHYSICAL WORLDEXERCISE - ASSIGNMENT (Section-B)
4 Videos
Similar Questions
Knowledge Check
A particle executing simple harmonic motion with time period T. the time period with which its kinetic energy oscillates is
ATB2TC4TDT2A particle executing SHM with time period T and amplitude A. The mean velocity of the particle averaged over quarter oscillation, is
AA4TB2ATC3ATD4AT
A particle executes shm with a period 8 s. Find the time in which half the total energy is potential.
View SolutionAmplitude of a particle executing SHM is a and its time period is T. Its maximum speed is
View SolutionA body is executing SHM with amplitude A and time period T. The ratio of kinetic and potential energy when displacement from the equilibrium position is half the amplitude
View SolutionThe amplitude of a particle executing SHM is made three-fourth keeping its time period constant. Its total energy will be
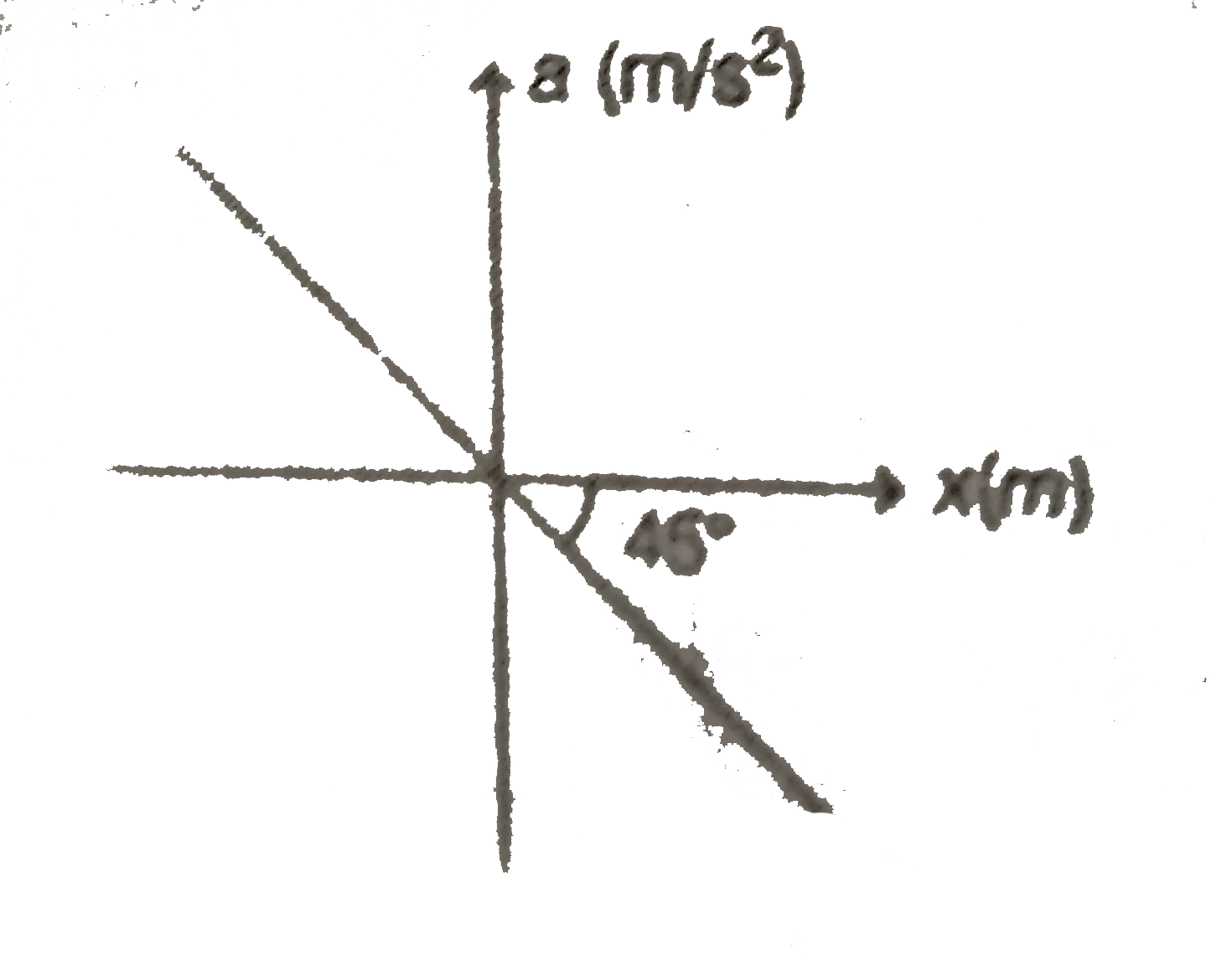
View SolutionAcceleration -displacemnet graph of a particle executing SHM is as shown in given figure. The time period of its oscillations is (in s)
View SolutionA particle executes SHM with time period T and amplitude A. The maximum possible average velocity in time T/4 is-
View Solution
