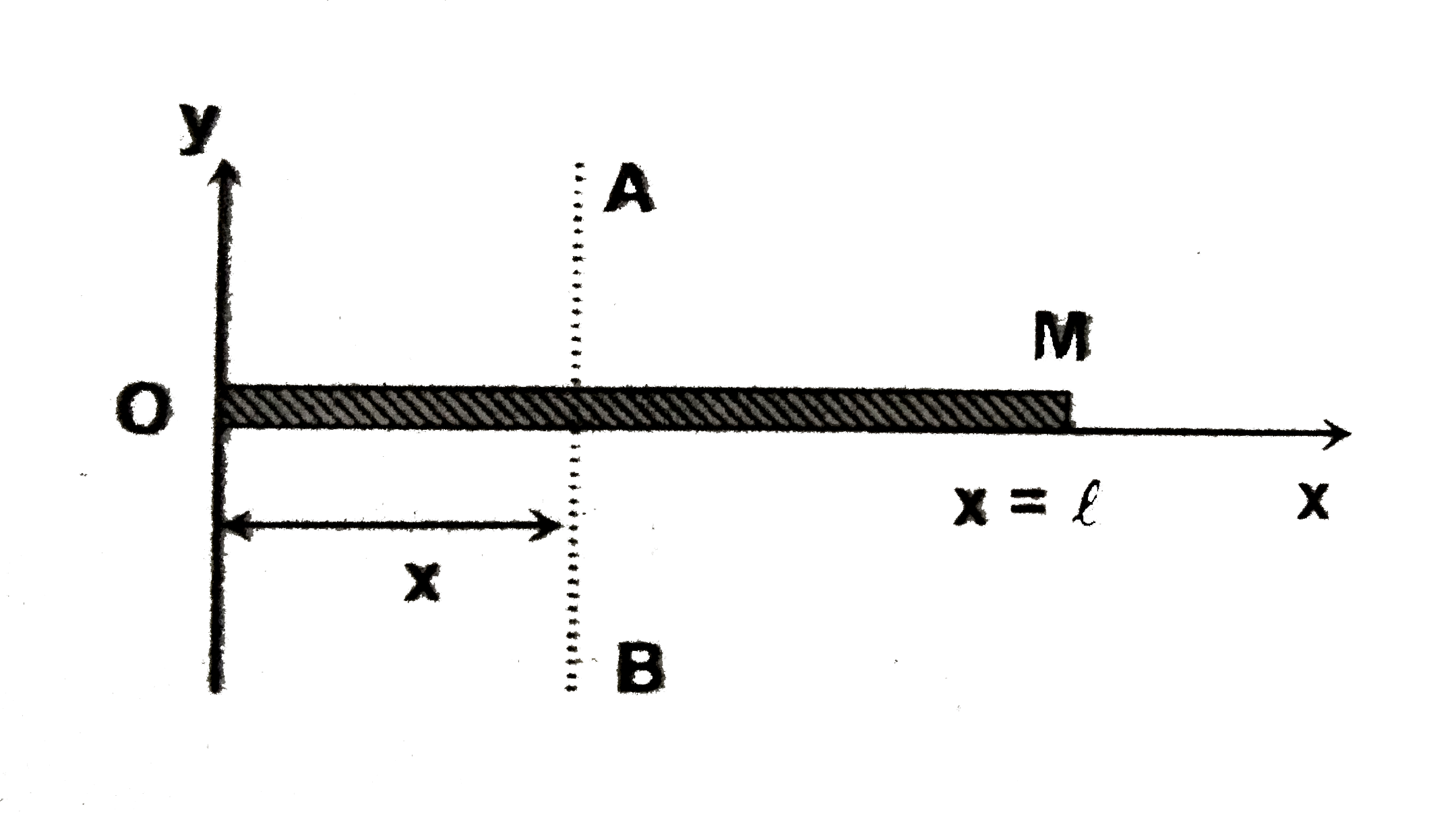
A non uniform rod OM (of length l m) is kept along x-axis and rotating about an axis AB, which is perpendicular to rod as shown in the figure. The rod has linear mass density that varies with the distance x from left end of the rod according to λ=λ0(x3L3)
Where unit of λ0 is kg/m. What is the value of x so that moment of inertia of rod about axis AB (IAB) is minimum?
7l15
2l5
8115
4l5
The correct Answer is:D
Step by step video, text & image solution for A non uniform rod OM (of length l m) is kept along x-axis and rotating about an axis AB, which is perpendicular to rod as shown in the figure. The rod has linear mass density that varies with the distance x from left end of the rod according to lamda=lamda_(0)((x^(3))/(L^(3))) Where unit of lamda_(0) is kg/m. What is the value of x so that moment of inertia of rod about axis AB (I_(AB)) is minimum? by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Similar Questions
A rod length L and mass M is placed along the x-axis with one end at the origin, as shown in the figure above. The rod has linear mass density λ=2ML2x, where x is the distance from the origin. Which of the following gives the x-coordinate of the rod's center of mass?
 View Solution
View SolutionLinear mass density of a rod AB(of≤n>h10m) varies with distance x from its end A as λ =λ0x3 (λ0 is positive constant) . Distance of centre of mass of the rod , from end B is
View SolutionFind centre of mass of given rod of linear mass density λ=(a+b(xl)2) , x is distance from one of its end. Length of the rod is l.
View SolutionA non–uniform thin rod of length L is placed along x-axis as such its one of ends at the origin. The linear mass density of rod is λ=λ0x. The distance of centre of mass of rod from the origin is :
View SolutionLinear mass density of a rod AB ( of length 10 m) varied with distance x from its end A as λ=λ0x3 (λ0 is poitive constant). Distance of centre of mass the rod, form end B is
View SolutionA uniform rod AB of length l and mass m is free to rotate about an Axis passing through A and perpendicular to length of the rod. The rod is released from rest as shown in figure. Given that the moment of inertia of the rod about A is ml23 The initial angular acceleration of the rod will be
 View Solution
View SolutionCalculate the moment of inertia of a rod of mass M, and length l about an axis perpendicular to it passing through one of its ends.
View SolutionThe density of a rod of length L varies as ρ=A+Bx where x is the distance from the left end. Locate the centre of mass.
 View Solution
View SolutionFind coordinates of mass center of a non-uniform rod of length L whose linear mass density lambda varies as lambda=a+bx, where x is the distance from the lighter end.
View SolutionThe linear mass density of a thin rod AB of length L varies from A to B as λ(x)=λ0(1+xL). Where x is the distance from A. If M is the mass of the rod then its moment of inertia about an axis passing through A and perpendicualr to the rod is :
View Solution

