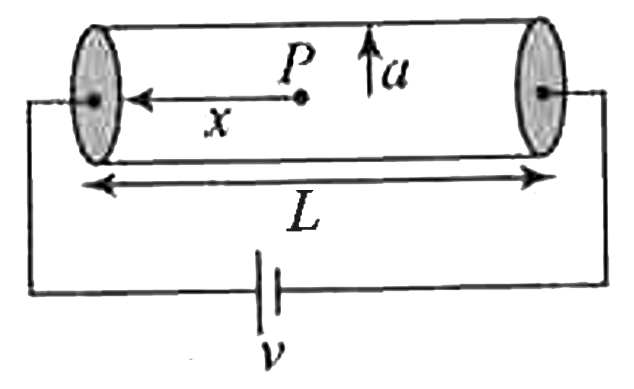
Two cylindrical rods of same cross-section area and same length are connected in series to an ideal cell as shown.The resistivity of left rod is ρ and that if right rod is 2ρ Then the variation of potential and electric field at any point P distant x from left end of combined rod system are given by
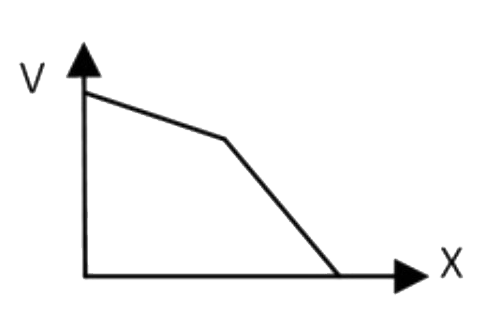
The correct Answer is:B
To solve the problem, we need to analyze the two cylindrical rods connected in series, taking into account their resistivities and how they affect the electric field and potential along the rods.
1. Identify the Parameters:
- Let the length of each rod be L.
- The resistivity of the left rod is ρ.
- The resistivity of the right rod is 2ρ.
- The cross-sectional area A of both rods is the same.
2. Calculate the Resistance of Each Rod:
- The resistance R of a rod is given by the formula:
R=ρLA
- For the left rod:
R1=ρLA
- For the right rod:
R2=2ρLA
3. Total Resistance in Series:
- The total resistance Rtotal of the two rods in series is:
Rtotal=R1+R2=ρLA+2ρLA=3ρLA
4. Current Through the Rods:
- If an ideal cell of voltage V is connected across the series combination, the current I through the rods can be calculated using Ohm's law:
I=VRtotal=VA3ρL
5. Electric Field in Each Rod:
- The electric field E in a rod is given by:
E=VL
- For the left rod:
E1=IR1L=I⋅ρLAL=IρA
- For the right rod:
E2=IR2L=I⋅2ρLAL=2IρA
6. Comparison of Electric Fields:
- Since E2=2E1, the electric field is greater in the right rod than in the left rod.
7. Potential Variation:
- The potential drop across each rod can be calculated as:
- For the left rod:
V1=E1⋅L
- For the right rod:
V2=E2⋅L
8. Total Potential:
- The total potential across both rods is:
V=V1+V2
9. Conclusion:
- The variation of potential and electric field at any point P (distance x from the left end) will show that the electric field is greater in the right rod, and the potential will be continuous across the junction of the two rods.
- Let the length of each rod be L.
- The resistivity of the left rod is ρ.
- The resistivity of the right rod is 2ρ.
- The cross-sectional area A of both rods is the same.
- The resistance R of a rod is given by the formula:
R=ρLA
- For the left rod:
R1=ρLA
- For the right rod:
R2=2ρLA
- The total resistance Rtotal of the two rods in series is:
Rtotal=R1+R2=ρLA+2ρLA=3ρLA
- If an ideal cell of voltage V is connected across the series combination, the current I through the rods can be calculated using Ohm's law:
I=VRtotal=VA3ρL
- The electric field E in a rod is given by:
E=VL
- For the left rod:
E1=IR1L=I⋅ρLAL=IρA
- For the right rod:
E2=IR2L=I⋅2ρLAL=2IρA
- Since E2=2E1, the electric field is greater in the right rod than in the left rod.
- The potential drop across each rod can be calculated as:
- For the left rod:
V1=E1⋅L
- For the right rod:
V2=E2⋅L
- The total potential across both rods is:
V=V1+V2
- The variation of potential and electric field at any point P (distance x from the left end) will show that the electric field is greater in the right rod, and the potential will be continuous across the junction of the two rods.
Similar Questions
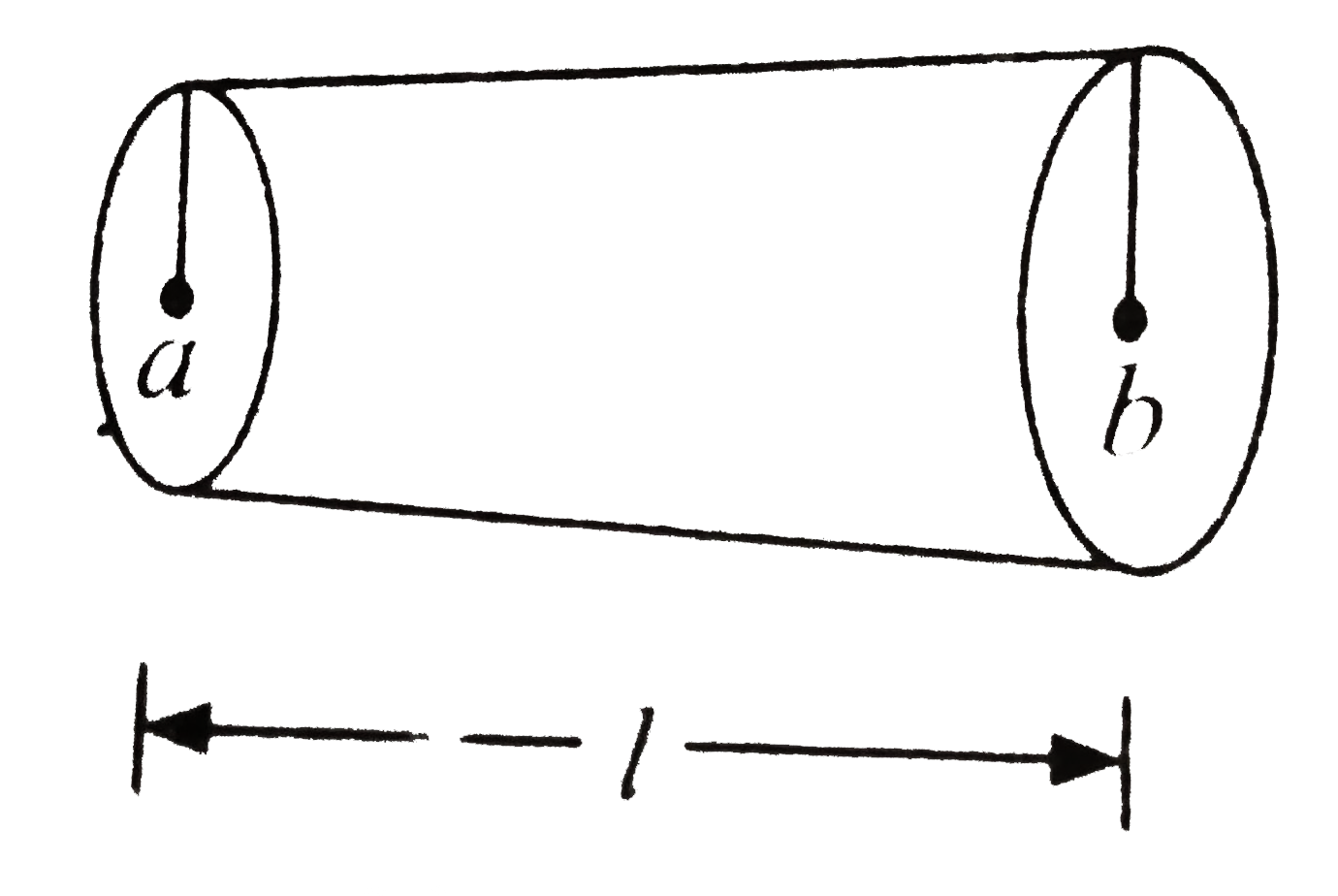
A conductor of resistivity ρ and resistance R, as shown in the figure, is connected across a battery of emf V. Its radius varies from a at left end to b at right end. The electric field at a point P at distance x from left end of it is
View SolutionTwo rods A and B of same cross-sectional area A and length l are connected in series between a source (T1=100∘C) and a sink (T2−0∘C) as shown in figure. The rod is laterally insulated.
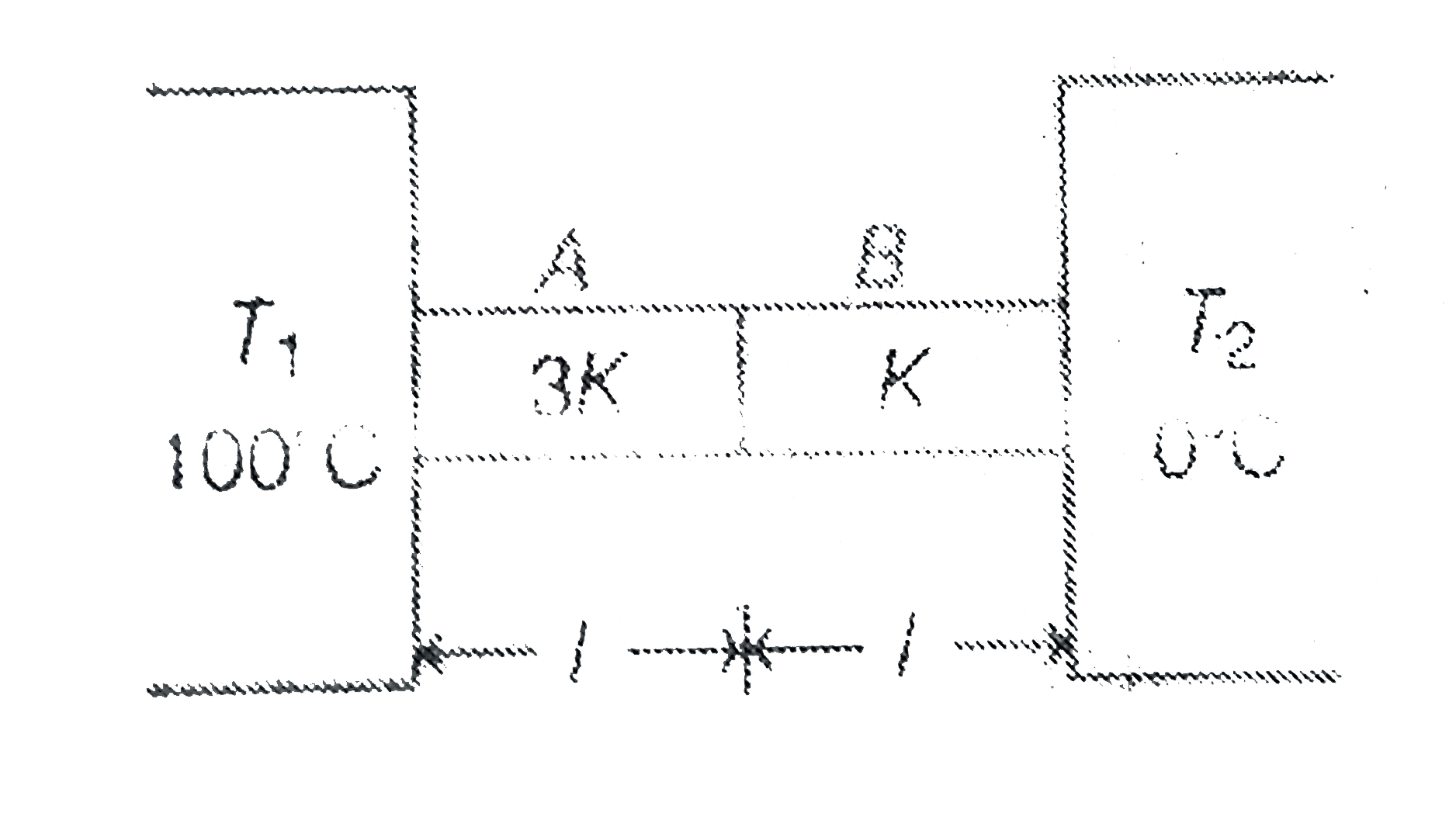
The ratio of the thermal resistance of the rods is
View SolutionA cylindrical solid of length L and radius a is connected across a source of emf V and negligible internal resistance shown in figure. The resistivity of the rod at point P at a distance x from left end is given by ρ=bx (where b is a positive constant). Find the electric field at point P.
View SolutionTwo rods A and B of same cross-sectional area A and length l are connected in series between a source (T1=100∘C) and a sink (T2−0∘C) as shown in figure. The rod is laterally insulated.

If TA and TB are the temperature drops across the rod A and B, then
View SolutionThree rods of same cross-section but different length and conductivity are joined in series . If the temperature of the two extreme ends are T1andT2(T1>T2) find the rate of heat transfer H.

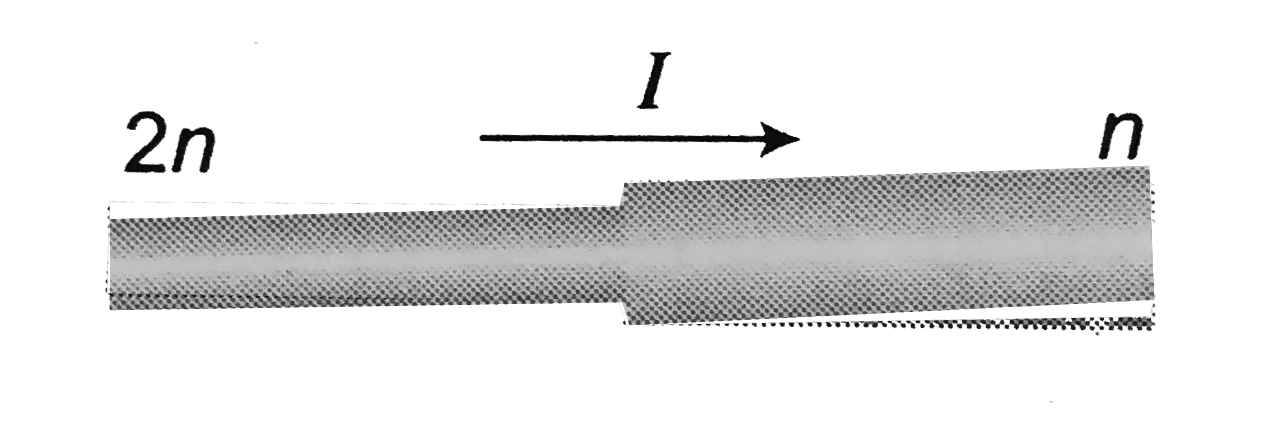
View SolutionTwo cylindrical rods of uniform cross-section area A and 2A, having free electrons per unit volume 2n and n respectively are joined in series. A current I flows through them in steady state. Then the ratio of drift velocity of free electron in left rod to drift velocity of electron in the
right rod is (vLvR) is
View Solution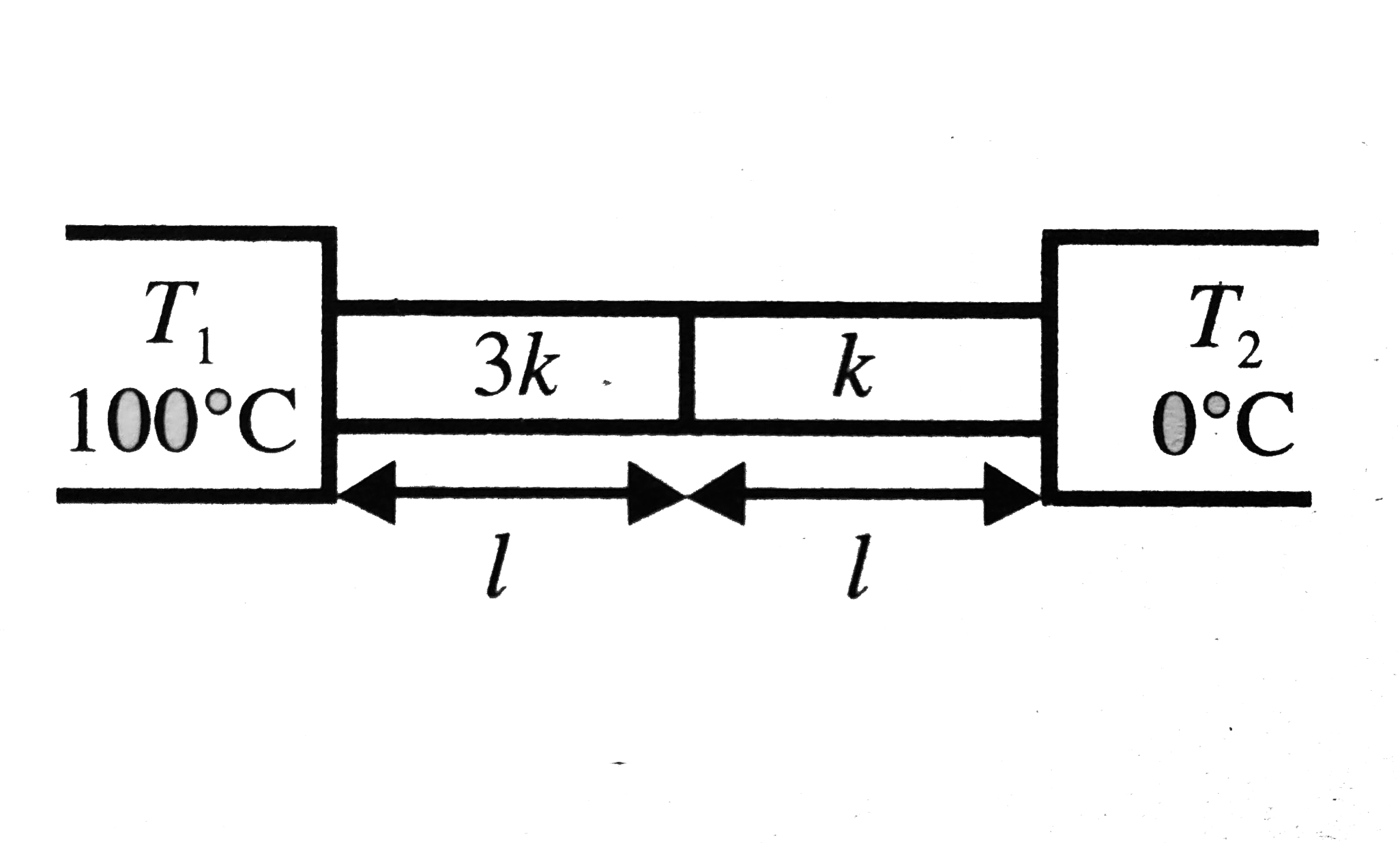
Two rods A and B of same length and cross-sectional area are connected in series and a temperature difference of 100∘C is maintained across the combination as shoen in Fig. If the thermal conductivity of the rod A is 3 k and that of rod B is k, Then
i.Determine the thermal resistance of each rod.
ii. determine the heat current flowing through each rod.
iii. determine the heat current flowing through each rod.
iv. plot the variation of temperature along the length of the rod.
View SolutionTwo rods A and B of same cross-sectional area A and length l are connected in series between a source (T1=100∘C) and a sink (T2−0∘C) as shown in figure. The rod is laterally insulated.
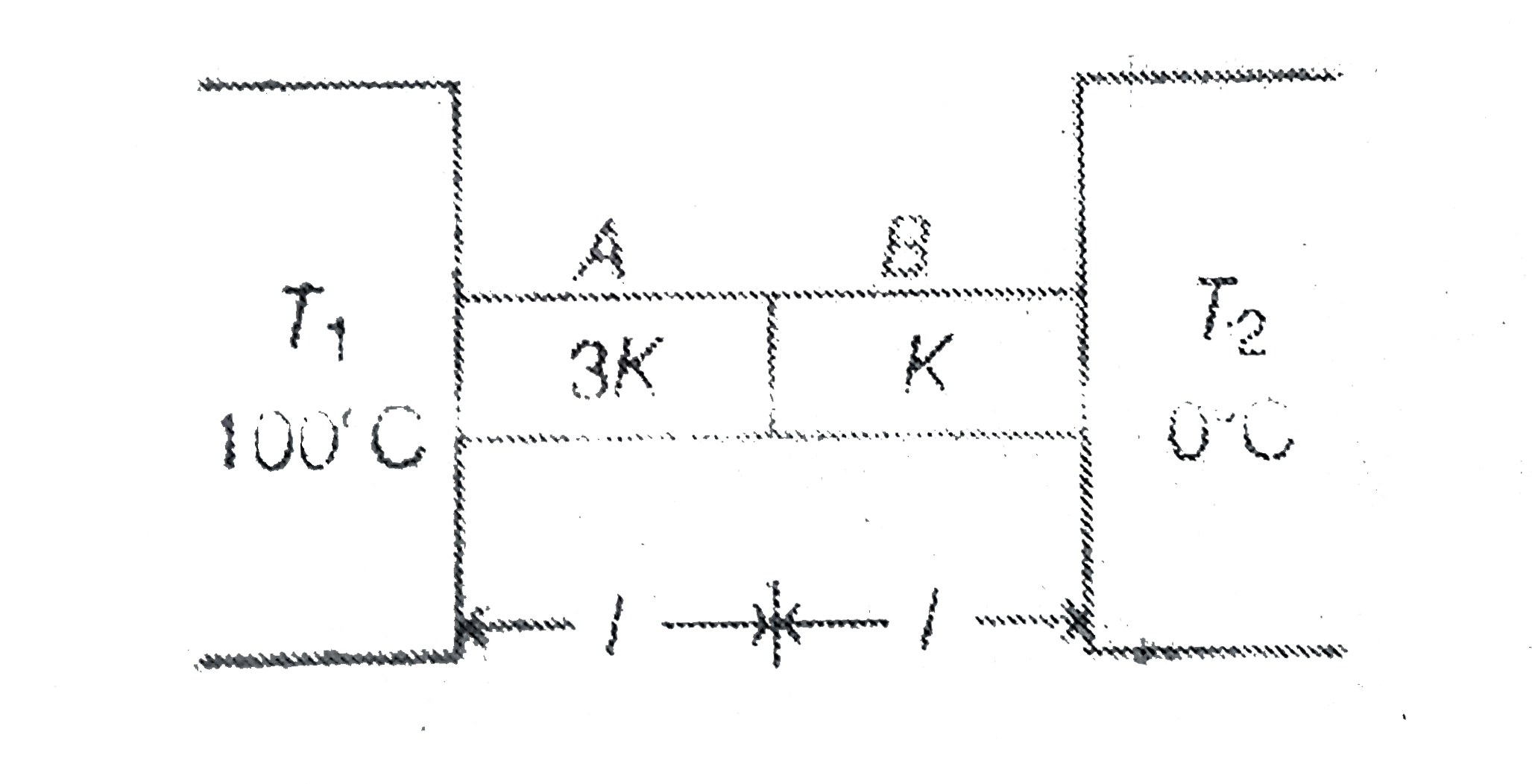
If GA and GB are the temperature gradients across the rod A and B, then
View SolutionA rod of length L and cross-section area A lies along the x-axis between x=0 and x=L. The material obeys Ohm's law and its resistivity varies along the rod according to ρ(x)=ρ0ε−x/L. The end of the rod x=0 is at a potential V0 and it is zero at x=L.
(a) Find the total resistance of the rod and the current in the wire.
(b) Find the electric potential in the rod as a function of x.
View Solution
Statement I: Two solid cylindrical rods of identical size and different thermal conductivity K1 and K2 are connected in series. Then the equivalent thermal conductivity of two rods system is less than that value of thermal conductivity of either rod.
Statement II: For two cylindrical rods of identical size and different thermal conductivity K1 and K2 connected in series, the equivalent thermal conductivity K is given by 2K=1K1+1K2
View Solution