A block starts moving up an inclined plane of inclination 30∘ with an initial velocity of v0 . It comes back to its initial position with velocity v02 . The value of the coefficient of kinetic friction between the block and the inclined plane is close to I1000 , The nearest integer to I is ____________ .
To solve the problem, we will apply the work-energy theorem and analyze the forces acting on the block as it moves up and down the inclined plane.
1. Identify the Forces:
- The gravitational force acting on the block is mg.
- The normal force N acting perpendicular to the inclined plane.
- The frictional force fk=μN acting opposite to the direction of motion.
2. Set Up the Geometry:
- The angle of inclination θ=30∘.
- The block moves a distance s up the incline and then back down.
3. Work Done Against Gravity and Friction:
- When the block moves up, the work done against gravity is Wg=mgssin(30∘)=mgs2.
- The work done against friction while moving up is Wf=−μmgcos(30∘)s=−μmgs√32.
4. Initial and Final Kinetic Energy:
- Initial kinetic energy when moving up: KEi=12mv20.
- Final kinetic energy when it reaches the top: KEf=0.
5. Applying Work-Energy Theorem for Upward Motion:
KEf−KEi=Wg+Wf
0−12mv20=mgs2−μmgs√32
Rearranging gives:
12mv20=mgs2−μmgs√32
6. Applying Work-Energy Theorem for Downward Motion:
- Initial kinetic energy when coming down: KEi=0.
- Final kinetic energy when it reaches the bottom: KEf=12m(v02)2=18mv20.
- The work done against gravity and friction while coming down is:
Wg=mgs2,Wf=−μmgs√32
Thus,
18mv20−0=mgs2−μmgs√32
7. Setting Up the Equations:
- From the upward motion:
12v20=gs−μgs√3
- From the downward motion:
18v20=gs−μgs√3
8. Equating the Two Expressions:
- Set the right-hand sides equal to each other:
12v20=18v20+μgs√3
Rearranging gives:
38v20=μgs√3
9. Solving for the Coefficient of Friction:
μ=3v208gs√3
10. Substituting Values:
- Given that the coefficient of kinetic friction is μ=I1000, we can find I.
11. Final Calculation:
- After substituting values and simplifying, we find that I is approximately 346.41.
- The nearest integer to I is 346.
Final Answer:
The nearest integer to I is 346.
- The gravitational force acting on the block is mg.
- The normal force N acting perpendicular to the inclined plane.
- The frictional force fk=μN acting opposite to the direction of motion.
- The angle of inclination θ=30∘.
- The block moves a distance s up the incline and then back down.
- When the block moves up, the work done against gravity is Wg=mgssin(30∘)=mgs2.
- The work done against friction while moving up is Wf=−μmgcos(30∘)s=−μmgs√32.
- Initial kinetic energy when moving up: KEi=12mv20.
- Final kinetic energy when it reaches the top: KEf=0.
KEf−KEi=Wg+Wf
0−12mv20=mgs2−μmgs√32
Rearranging gives:
12mv20=mgs2−μmgs√32
- Initial kinetic energy when coming down: KEi=0.
- Final kinetic energy when it reaches the bottom: KEf=12m(v02)2=18mv20.
- The work done against gravity and friction while coming down is:
Wg=mgs2,Wf=−μmgs√32
Thus,
18mv20−0=mgs2−μmgs√32
- From the upward motion:
12v20=gs−μgs√3
- From the downward motion:
18v20=gs−μgs√3
- Set the right-hand sides equal to each other:
12v20=18v20+μgs√3
Rearranging gives:
38v20=μgs√3
μ=3v208gs√3
- Given that the coefficient of kinetic friction is μ=I1000, we can find I.
- After substituting values and simplifying, we find that I is approximately 346.41.
- The nearest integer to I is 346.
The nearest integer to I is 346.
Topper's Solved these Questions
Similar Questions
A block starts moving up a fixed inclined plane of inclination 60∘C with a velocityof 20ms−1 and stops after 2s. The approximate value of the coefficient of friction is [g=10ms−2]
View SolutionA block slides down on inclined plane (angle of inclination 60∘ ) with an accelration g/2 Find the coefficient friction

View Solution
Knowledge Check
A solid cylinder rolls up an inclined plane of inclination θ with an initial velocity v. How far does the cylinder go up the plane ?
A3v22gsinθBv24gsinθC3v2gsinθD3v24gsinθ
Block of mass 10 kg is moving on inclined plane with constant velocity 10 m/s. The coedfficient of kinetic friction between incline plane and block is :-
View SolutionAn ice cube is kept on an inclined plane of angle 30∘. The coefficient to kinetic friction between the block and incline plane is the 1/√3. What is the acceleration of the block ?
View SolutionA particle is projected directly along a rough plane of inclination θ with velocity u. If after coming to the rest the particle returns to the starting point with velocity v, the coefficient of friction between the partice and the plane is
View SolutionA block starts going up a rough inclined plane with velocity V0 as shown in figure.After some time reaches to starting point again, with a velocity V02.Find coefficient of friction μ .Given g=10msec2.
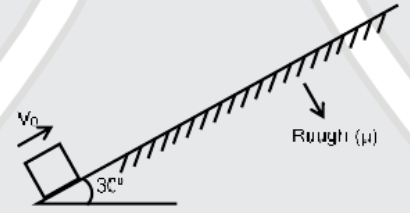
View Solution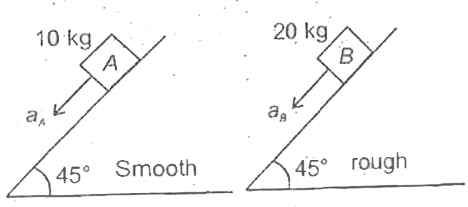
The ratio of acceleration of blocks A placed on smooth incline with block B placed on rough incline is 2:1. The coefficient of kinetic friction between block B and incline is
View SolutionA block of mass 4kg rests on an an inclined plane. The inclination of the plane is gradually increased. It is found that when the inclination is 3 in 5 (sin=θ35) the block just begins to slide down the plane. The coefficient of friction between the block and the plane is.
View SolutionA block of mass m is given an initial downward velocity v0 and left on inclined place ( coefficient of friction =0.6). The block will
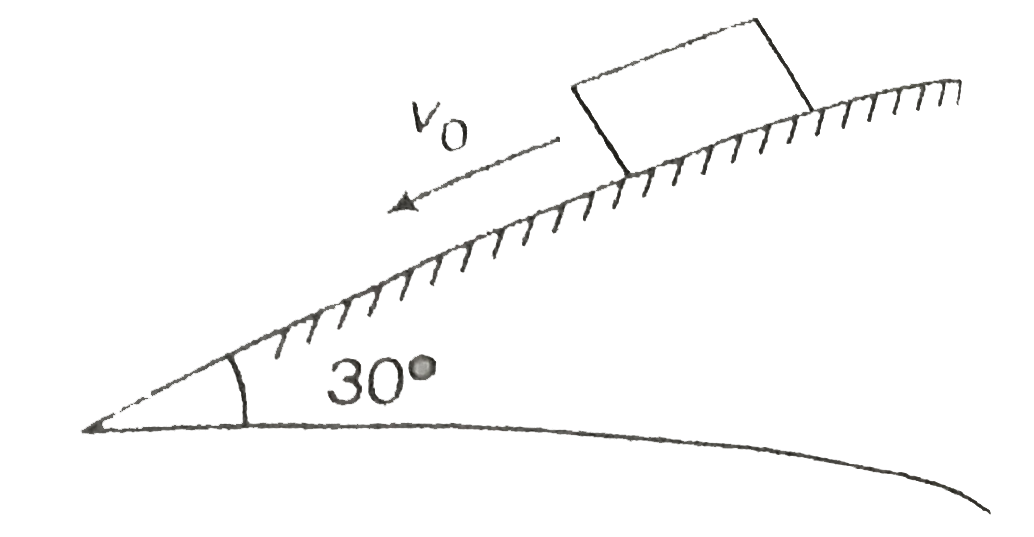
View Solution
