The figure shows an overhead view of a corridor with a plane mirror MN mounted at one end. A burglar B sneaks along the corridor directly towards the centre of the mirror. If d = 3m, how far from the mirror will the burglar be when the security guard S can first see him in the mirror ? ---
3.0m
4.5m
6.0m
1.5m
The correct Answer is:D
To solve the problem, we need to determine how far the burglar B will be from the mirror when the security guard S can first see him in the mirror.
1. Understanding the Setup:
- We have a corridor with a mirror at one end.
- The distance from the burglar to the mirror is denoted as x.
- The total distance from the burglar to the point directly opposite the mirror (where the guard can see) is d=3m.
2. Identifying the Geometry:
- The burglar is moving towards the mirror, and the guard can see the burglar in the mirror when the light reflects off the mirror.
- The distance from the mirror to the point directly opposite the burglar is d2=32=1.5m.
3. Using the Law of Reflection:
- According to the law of reflection, the angle of incidence is equal to the angle of reflection.
- When the burglar is at a distance x from the mirror, the angle formed with the line of sight to the guard can be analyzed.
4. Setting Up the Triangles:
- We can create two right triangles:
- Triangle 1: The triangle formed by the burglar, the point directly opposite the burglar, and the mirror.
- Triangle 2: The triangle formed by the guard, the mirror, and the line of sight to the burglar.
5. Applying Trigonometry:
- In Triangle 1, we can express cot(θ) as:
cot(θ)=xd2=2xd
- In Triangle 2, we have:
cot(θ)=dd=1
6. Equating the Two Expressions:
- From the two triangles, we have:
2xd=1
- Rearranging gives:
2x=d
- Therefore:
x=d2
7. Substituting the Value of d:
- Given d=3m:
x=32=1.5m
Conclusion:
The burglar will be 1.5m away from the mirror when the security guard can first see him in the mirror.
- We have a corridor with a mirror at one end.
- The distance from the burglar to the mirror is denoted as x.
- The total distance from the burglar to the point directly opposite the mirror (where the guard can see) is d=3m.
- The burglar is moving towards the mirror, and the guard can see the burglar in the mirror when the light reflects off the mirror.
- The distance from the mirror to the point directly opposite the burglar is d2=32=1.5m.
- According to the law of reflection, the angle of incidence is equal to the angle of reflection.
- When the burglar is at a distance x from the mirror, the angle formed with the line of sight to the guard can be analyzed.
- We can create two right triangles:
- Triangle 1: The triangle formed by the burglar, the point directly opposite the burglar, and the mirror.
- Triangle 2: The triangle formed by the guard, the mirror, and the line of sight to the burglar.
- In Triangle 1, we can express cot(θ) as:
cot(θ)=xd2=2xd
- In Triangle 2, we have:
cot(θ)=dd=1
- From the two triangles, we have:
2xd=1
- Rearranging gives:
2x=d
- Therefore:
x=d2
- Given d=3m:
x=32=1.5m
The burglar will be 1.5m away from the mirror when the security guard can first see him in the mirror.
Similar Questions
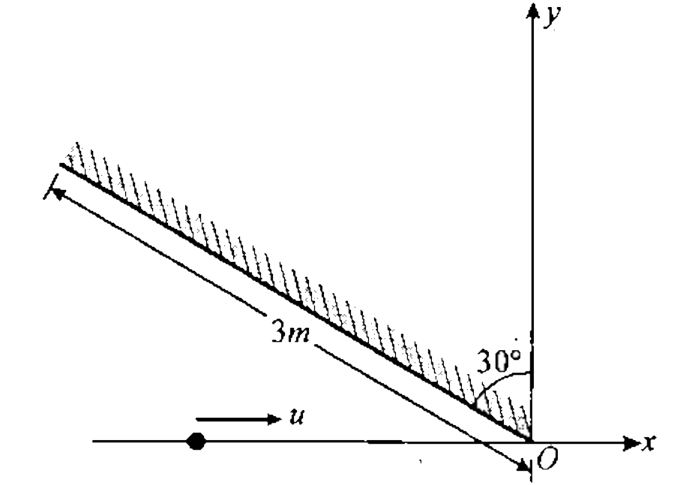
A plane mirror is placed with its plane at an angle 30∘ with the y-axis. Plane of the mirror is perpendicular to the xy-plane and the length of the mirror is 3m. An insect moves along x-axis starting from a distant point, with speed 2 cm/s. The duration of the time for which the insect can see its shown image in the mirror is:
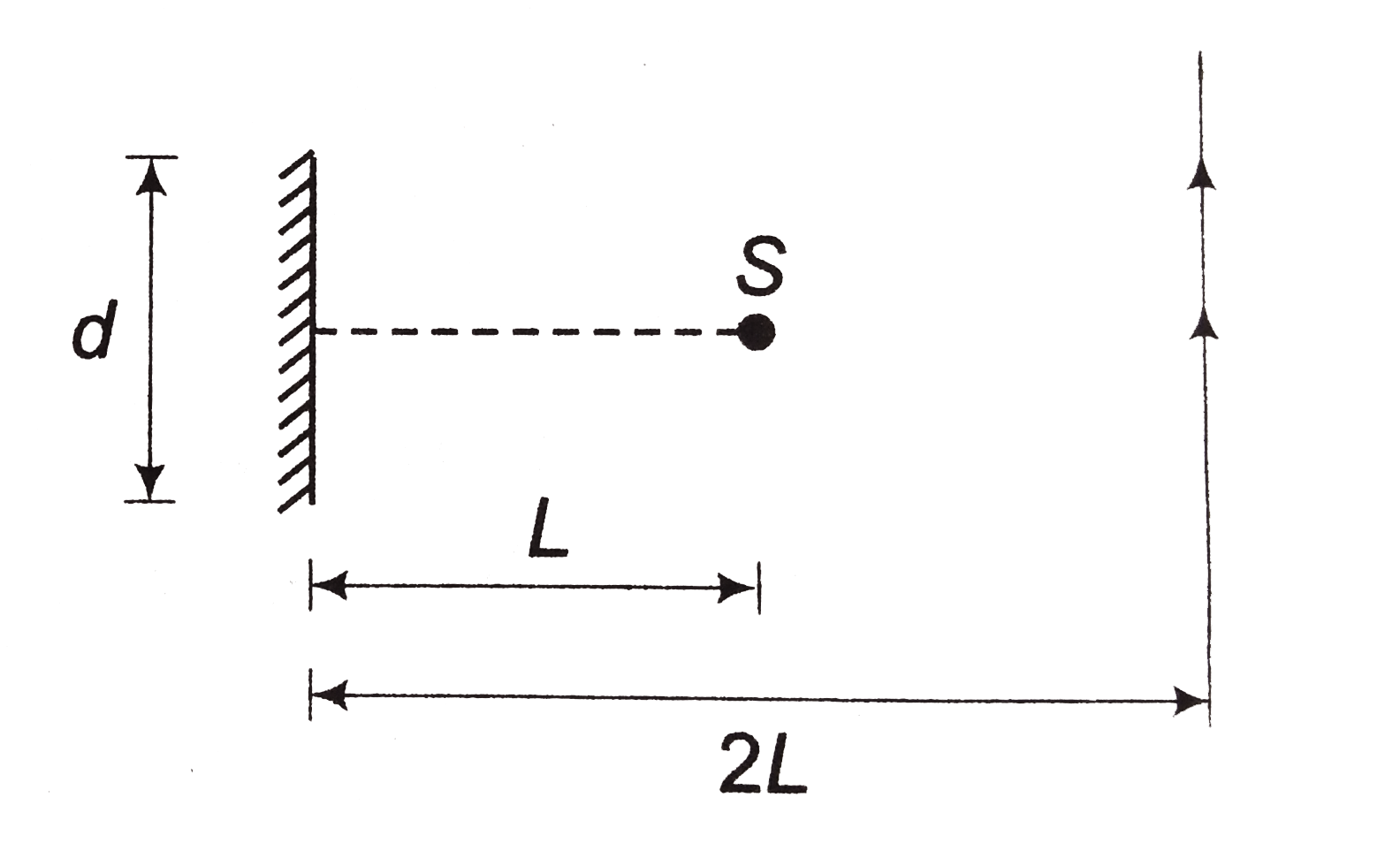
View SolutionA point source of light S, placed at a
distance L in front of the centre of a mirror of width d,
hangs vertically on a wall. A man walks in front of the
mirror along a line parallel to th mirror at a distane
2L form it as shown.The greatest distance over which
he can see the image of the light source in the mirror is
(a) d/2 (b) d (c) 2d (d) 3 d.
View SolutionA point source of light S, placed at a
distance L in front of the centre of a mirror of width d,
hangs vertically on a wall. A man walks in front of the
mirror along a line parallel to th mirror at a distane
2L form it as shown.The greatest distance over which
he can see the image of the light source in the mirror is
(a) d/2 (b) d (c) 2d (d) 3 d.

View SolutionA point source of light S is placed at a distance 10 cm in front of the centre of a mirror of width 20 cm suspended vertically on a wall. An insect walks with a speed 10cm/s in front of the mirror along a line parallel to the mirror at a distance 20 cm from it as shown in figure. find the maximum time during which the insect can see the image of the source S in the mirror.
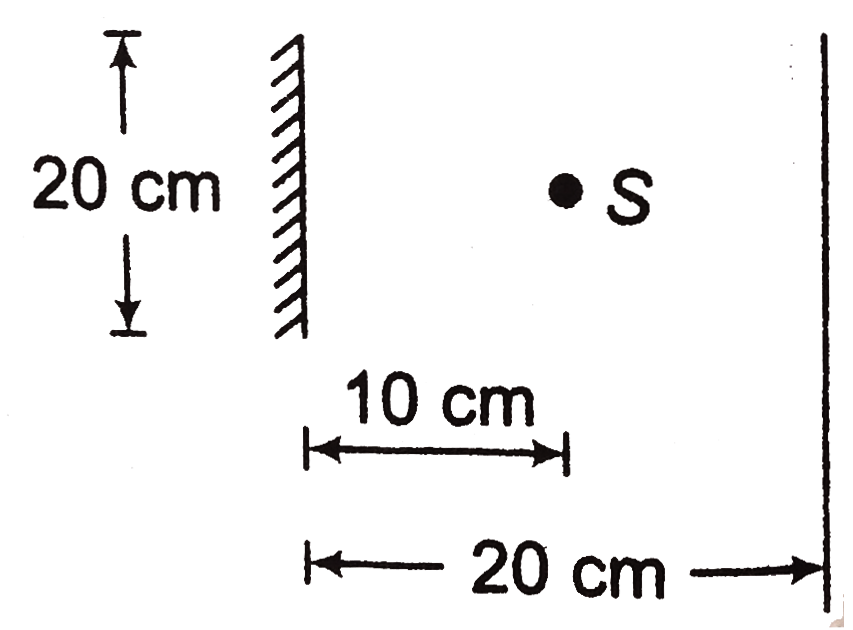
View SolutionIn a Lloyds's mirror experiment as narrow slit S transmitting a light of wavelength λ is placed 3 mm above a small plane mirror ( as shown). The light coming directly from the the slit and that coming after the reflection interfere on a screen placed at a distance of 90 cm from the slit. Length of mirror is 2 mm and the middle point of mirror is 2 mm from point P.
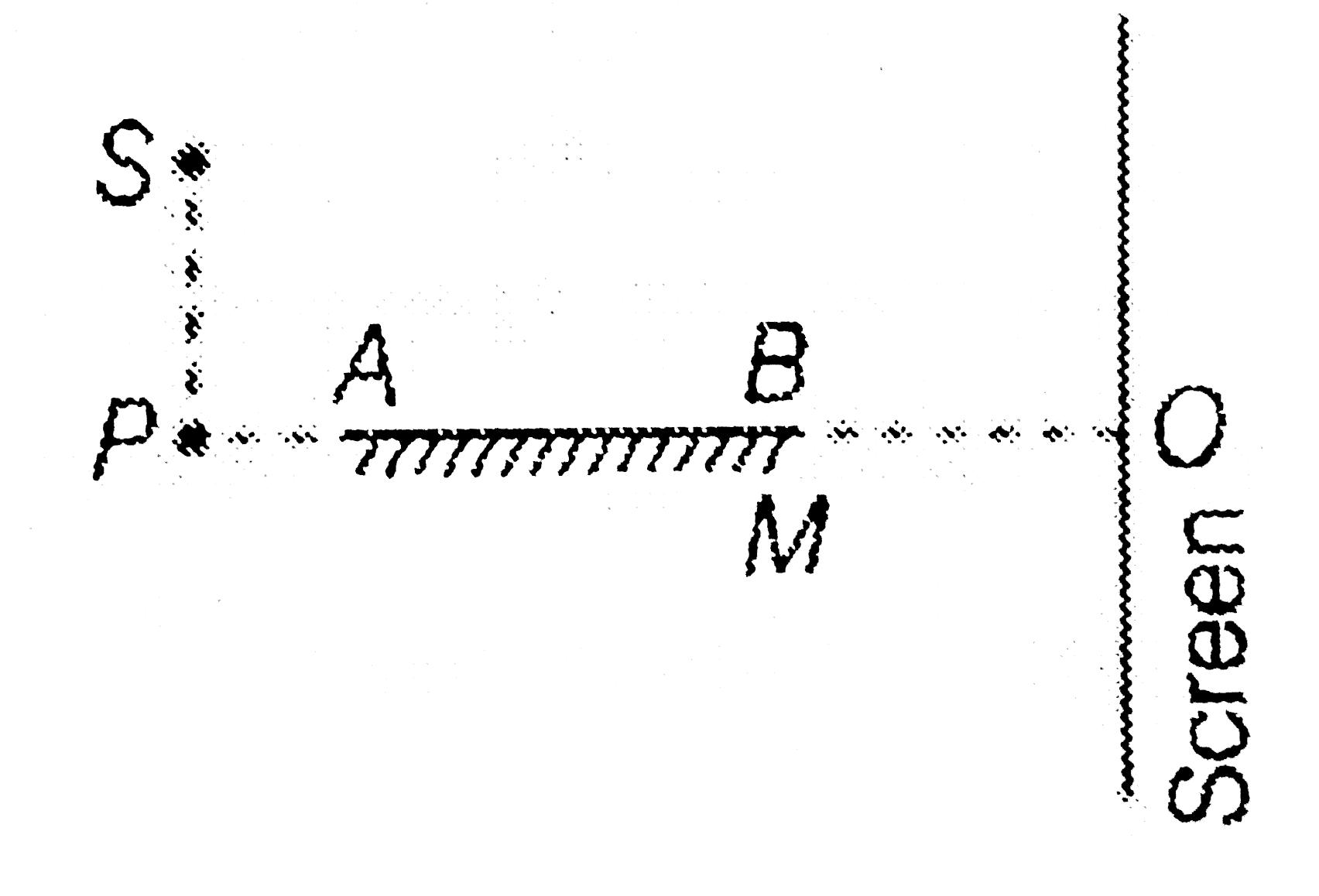
If the mirror is shifted towards left then how does the fringe pattern on screen changes ?
View SolutionA narrow slit S transmitting light of wavelength λ is placed a distance d above a large plane mirror as shown in figure. The light coming directly from the slit and that coming after the reflection interference at a screen ∑ placed at a distance LD from the slit. a. What will be the intensity at a point just above the mirror. i.e., just above O? b. At what distance from O does the first maximum occur?
?
View SolutionTwo long parallel horizontal rails a, a distance d aprt and each having a risistance λ per unit length are joing at one end by a resistance R. A perfectly conduction rod MN of mass m is free to slide along the rails without friction (see figure). There is a uniform magnetic field of induction B normal to the plane of the paper and directed into the paper. A variable force F is applied to the rod MN such that, as the rod moves a constant current flows through R.
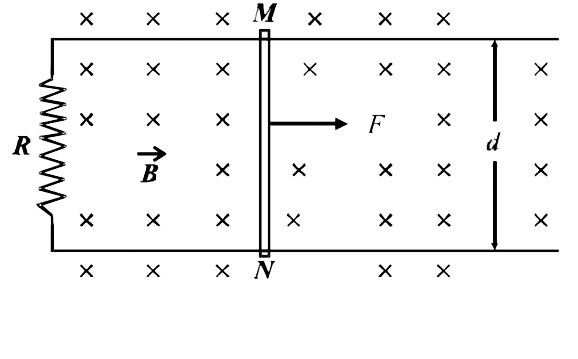
(i) Find the velocity of the rod and the applied force F as function of the distance x of the rod from R.
(ii) What fraction of the work done per second by F is converted into heat?
View SolutionA man of height =3/2m,wants to see himself in plane mirror from top to bottom. The plane mirror is inclined with vertical wall at angle α=53∘. If the least size of mirror to see him 3nm, the distance of eye from mirror is d=3m, find the value of m
View SolutionP is small angled prism of angle 3∘ made of a material of refractive index 1.5. A ray of light is incident normally to the mirror as shown in figure. M is a plane mirror. The angle of deviation for the ray reflected from the mirror M with respect to the incident ray is :
A. 4.5∘
B. 175.3∘
C. 177∘
D. 178.5∘
View SolutionA thin equiconvex lens made of glass of refractive index 3/2 and of focal length 0.3m in air is sealed into an opening at one end of a tank filled with water (μ=32). On the opposite side of the lens, a mirror is placed inside the tank on the tank wall perpendicular to the lens axis as shown in Figure. The separation between the lens and mirror is 0.8m. A small object is placed outside the tank in front of the lens at a distance oa 0.9m from the lens along its axis. Find the position (relative to lens) of the image of the object formed by the system.

View Solution
