VBB can vary between 0 and 5 V. Find the minimum value of base current and VBB, so that transistor works in saturation mode. [Given β=200andVBE=1V]
20μA,2.8V
25μA,3.5V
20μA,3.5V
25μA,2.8V
The correct Answer is:C
Step by step video & image solution for V_("BB") can vary between 0 and 5 V. Find the minimum value of base current and V_("BB"), so that transistor works in saturation mode. ["Given "beta =200 and V_("BE")=1V] by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Similar Questions
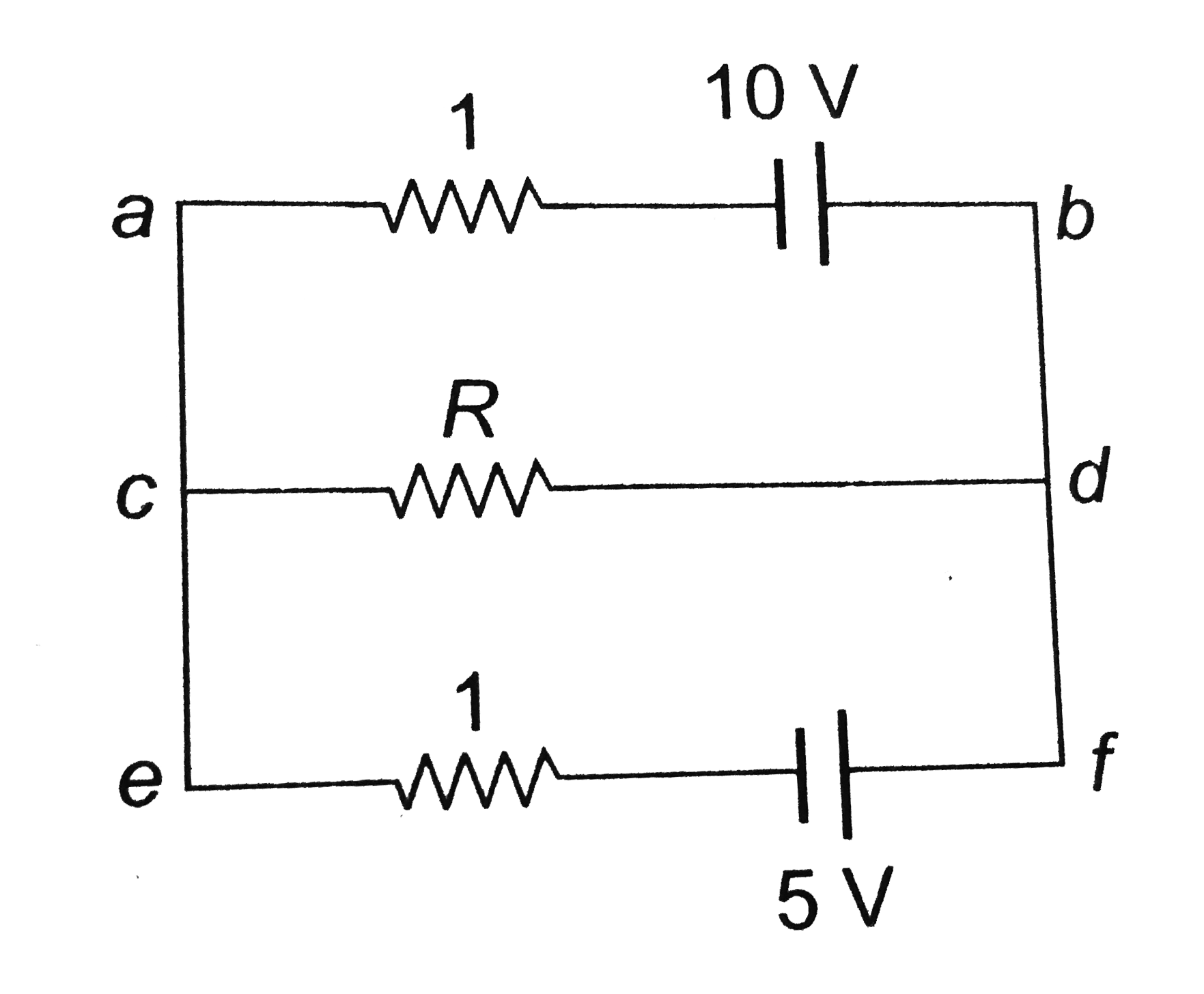
Find the value of R for which no current will flow through 5V battery
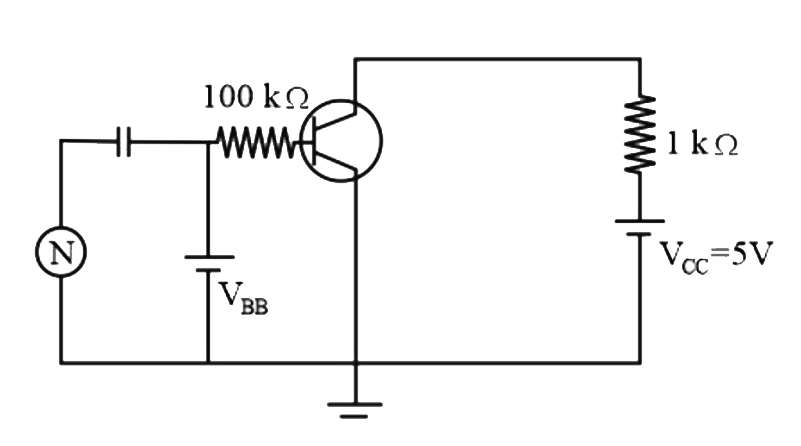
View SolutionIn common emitter transistor as shown in Fig., the VBB supply can be varied from 0 V to 5.0V. The Si. Transistor has βac=250 and RB=100kΩ,Rc=1kΩ,VCC=5.0V. Assume that when the transistor is saturated, VCE=0V and VBE=0.8V. Calculate the minimum base current, for which the transistor will reach saturation. Hence, determine Vi when the transistor is 'switched on' find ranges of Vi for which the transistor is switched off and switched on.
View Solution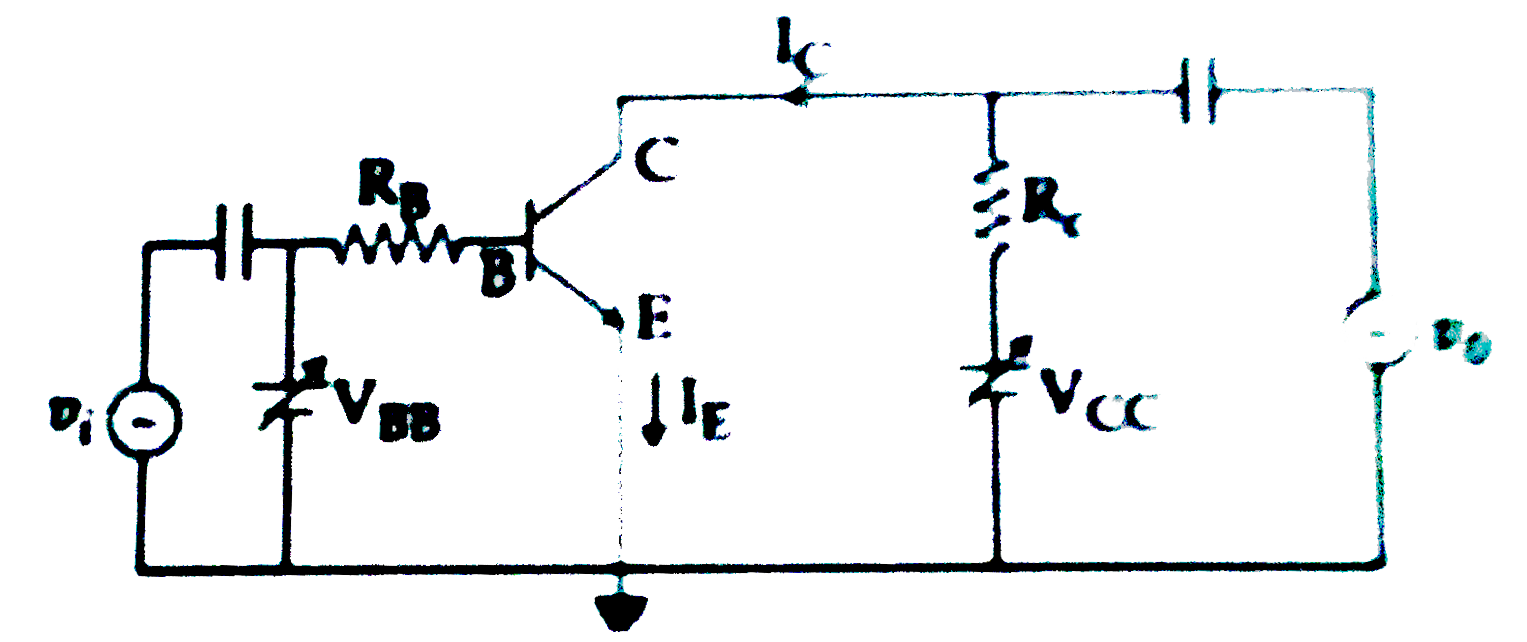
In the figure, given that VBB supply can vary from 0 to 5.0V,VC=5V,βdc=200,RB=100KΩ,RC=1KΩ and VBE=1.0V, The minimum base current and the input voltage at which the transistor will go to saturation, will be, respectively:
View SolutionIn a common emitter transistor circuit, the base current is 40μA , then VBE is
View SolutionFind the potential difference Va−Vb between the points (1) and (2) shown in each part of Fig.
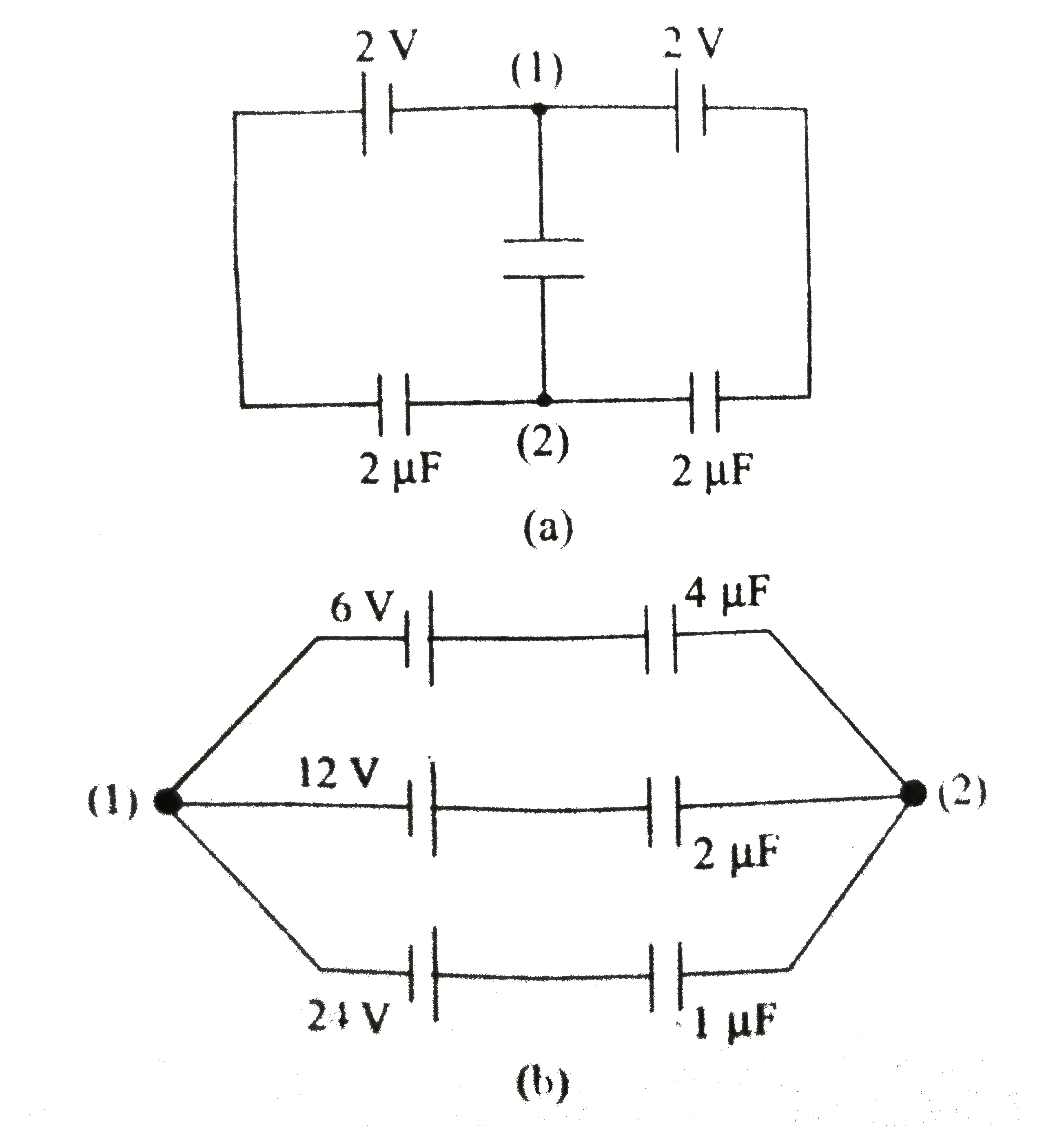
View SolutionConsider the circuit arrangnent shown in Fig. for studying input and output characteristics of npn transistor in CE configuration.
Select the values of R and R for a transistor whose VBE=0.7V, so that the transistor is operating at point Q as shown in the characteristics shown in Fig.
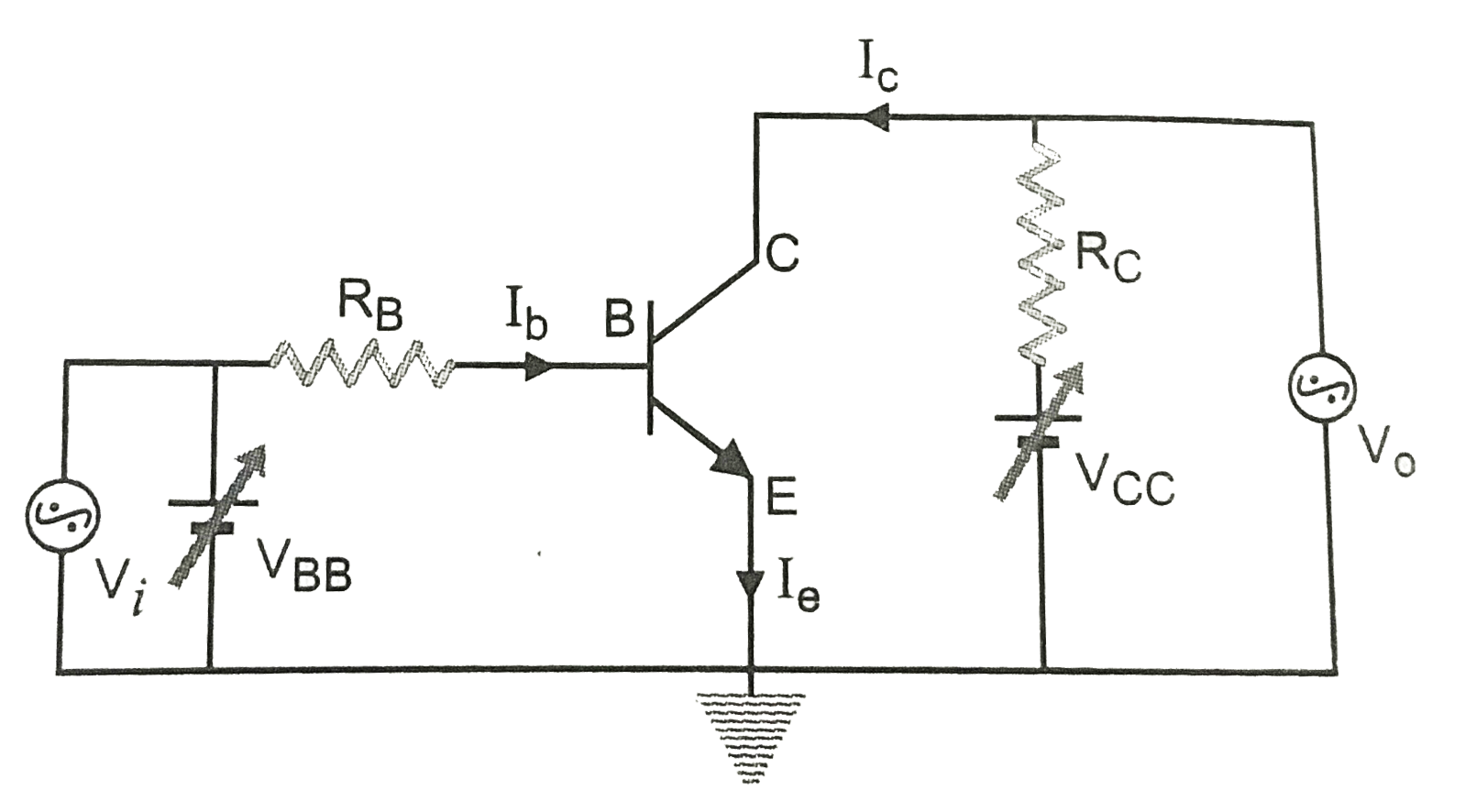
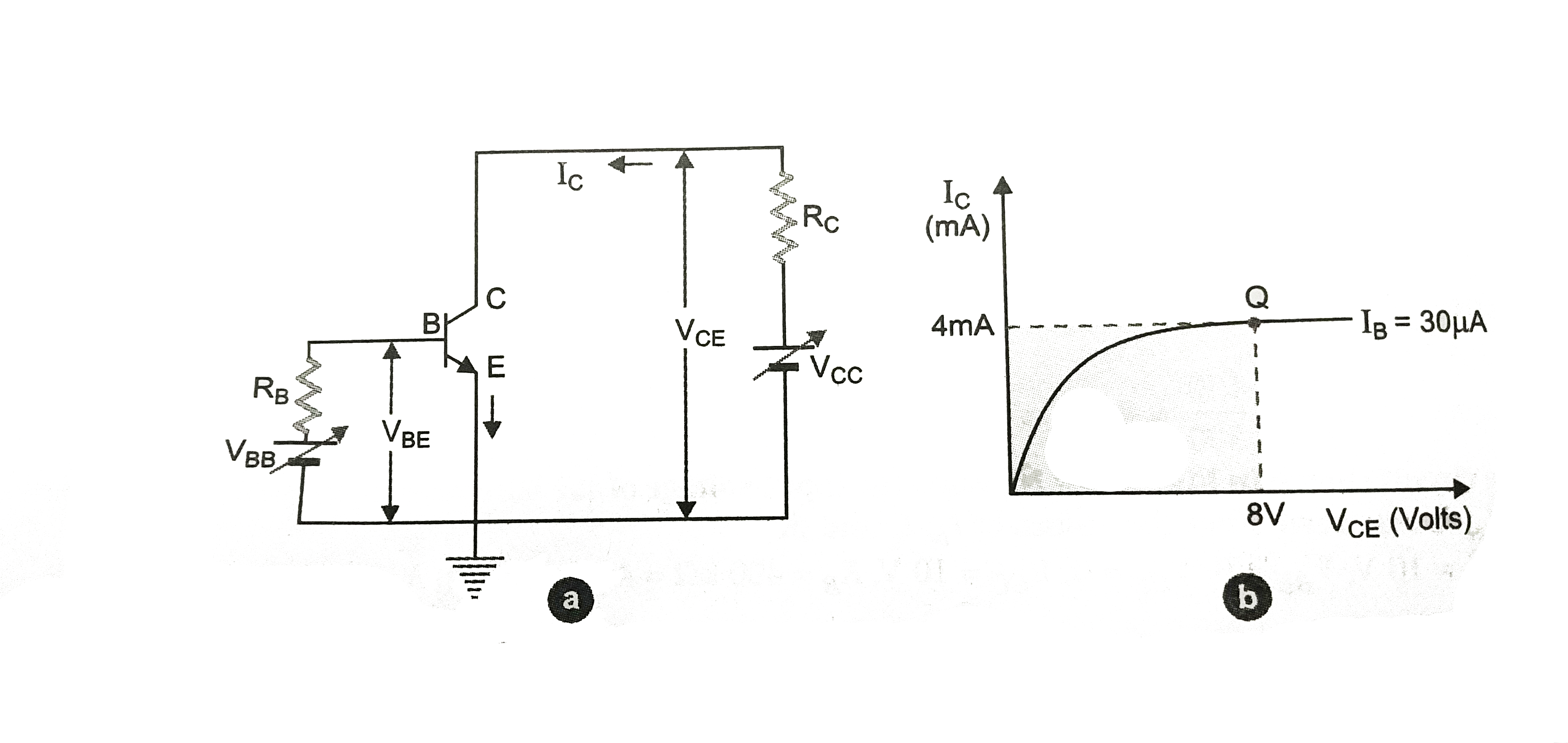Given that the input impedance of the transistor is very small and VCC=VBB=16V, also find the voltage gain and power gain of circuit making appropriate assumptions.
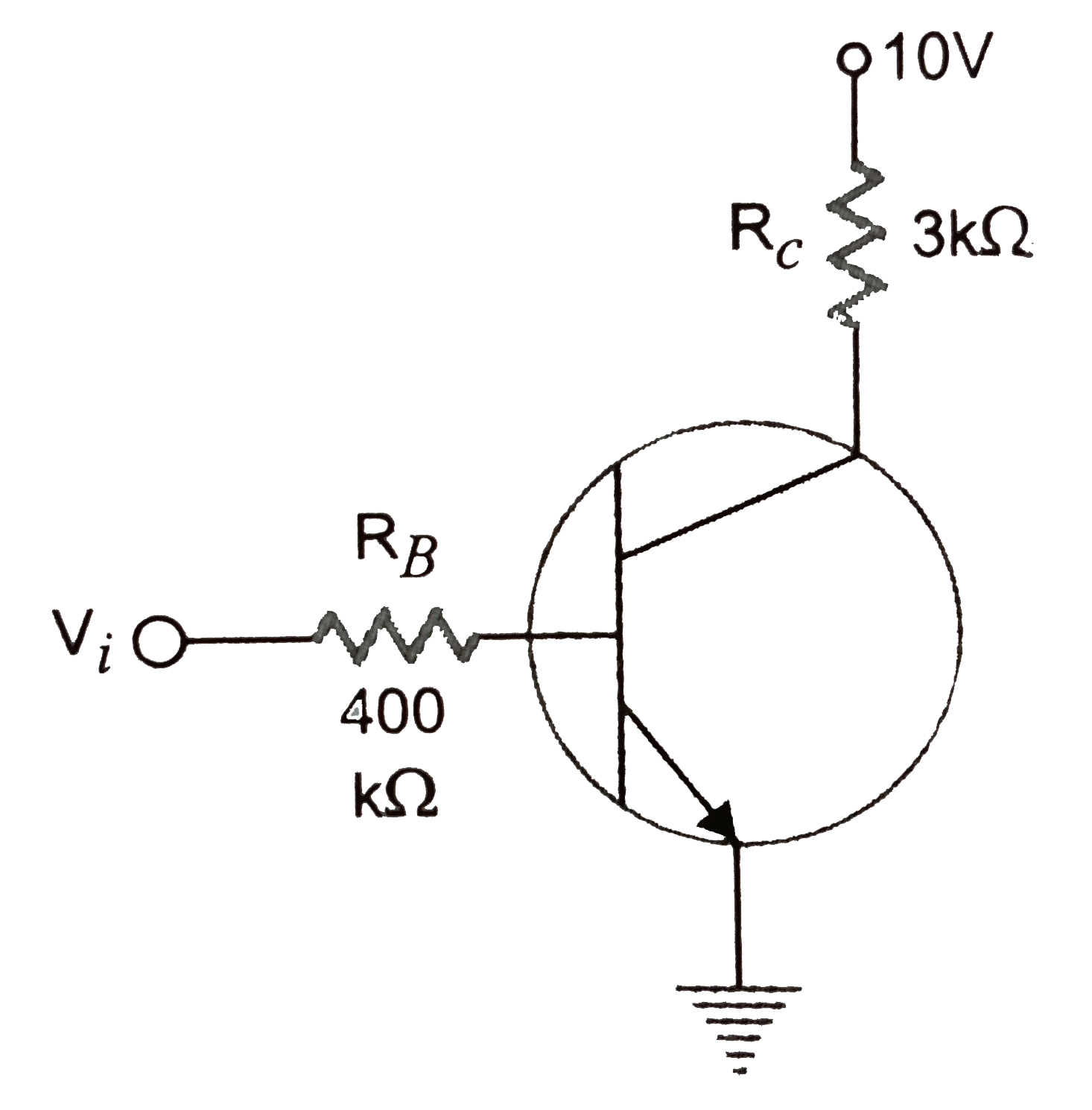
View SolutionIn the circuit shown in Fig. when the input voltage of the base resistance is 10V,Vbe is zero and Vce is also zero. Find the values of I,I and β.
View SolutionGraphical soluton of a two body head on collision
A block A of mass m moving with a uniform velocity v0 strikes another identical block B kept at rest on a horizontal smooth surface as shown in the figure (i). We can conserve linear momentum.
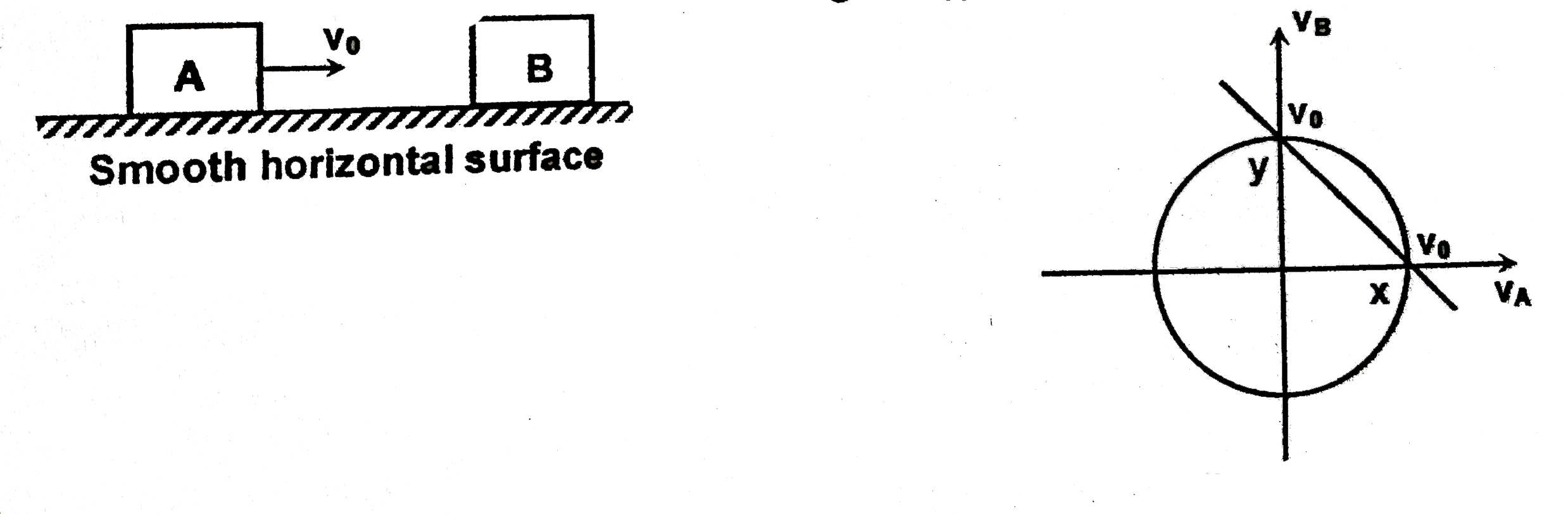
So mv0=mvAmvB (vA and vB are the velocities of the blocks after collision)
∴v0=vA+vB.........(i)
If the collision is perfectly elastic
12mv20=12mv2A+12mv2B
⇒v20=v2A+v2B......(ii)
Both the above equation (i) and (ii) are plotted on vA−vB plane as shown in figure (ii). This plot can be used to find the unknowns vA and vB.
For example the solution of the situation in figure (i) is vA=0,vB=v0 (point y in the plot)
Because vA=v0,vB=0 (point x in the plot) is not physically possible.
In a situation block A is moving with velocity 2m/s an strikes another identical block B kept at rest. The vA−vB plot for the situation is shown. m and l are the intersection points whose vA,vB coordinaes are given in the figure. The coefficient of restitution of the collision is
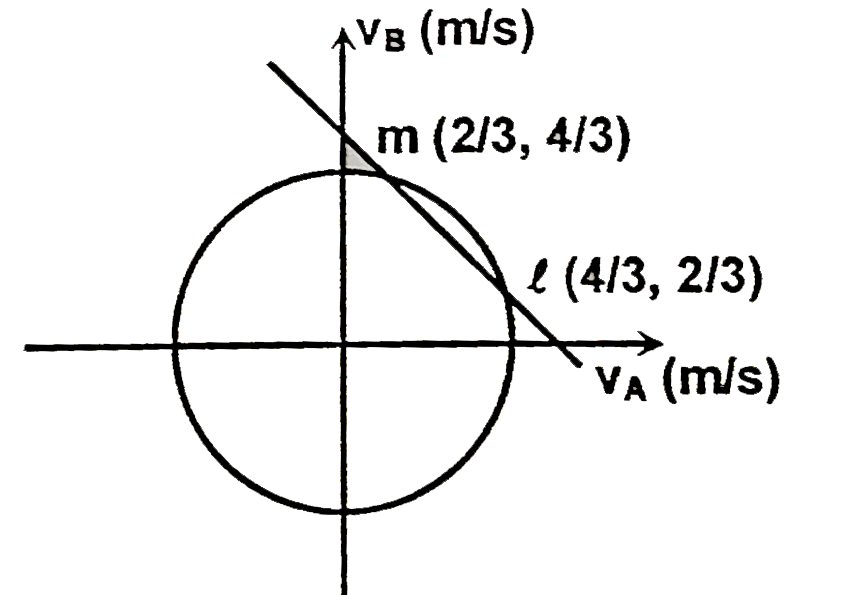
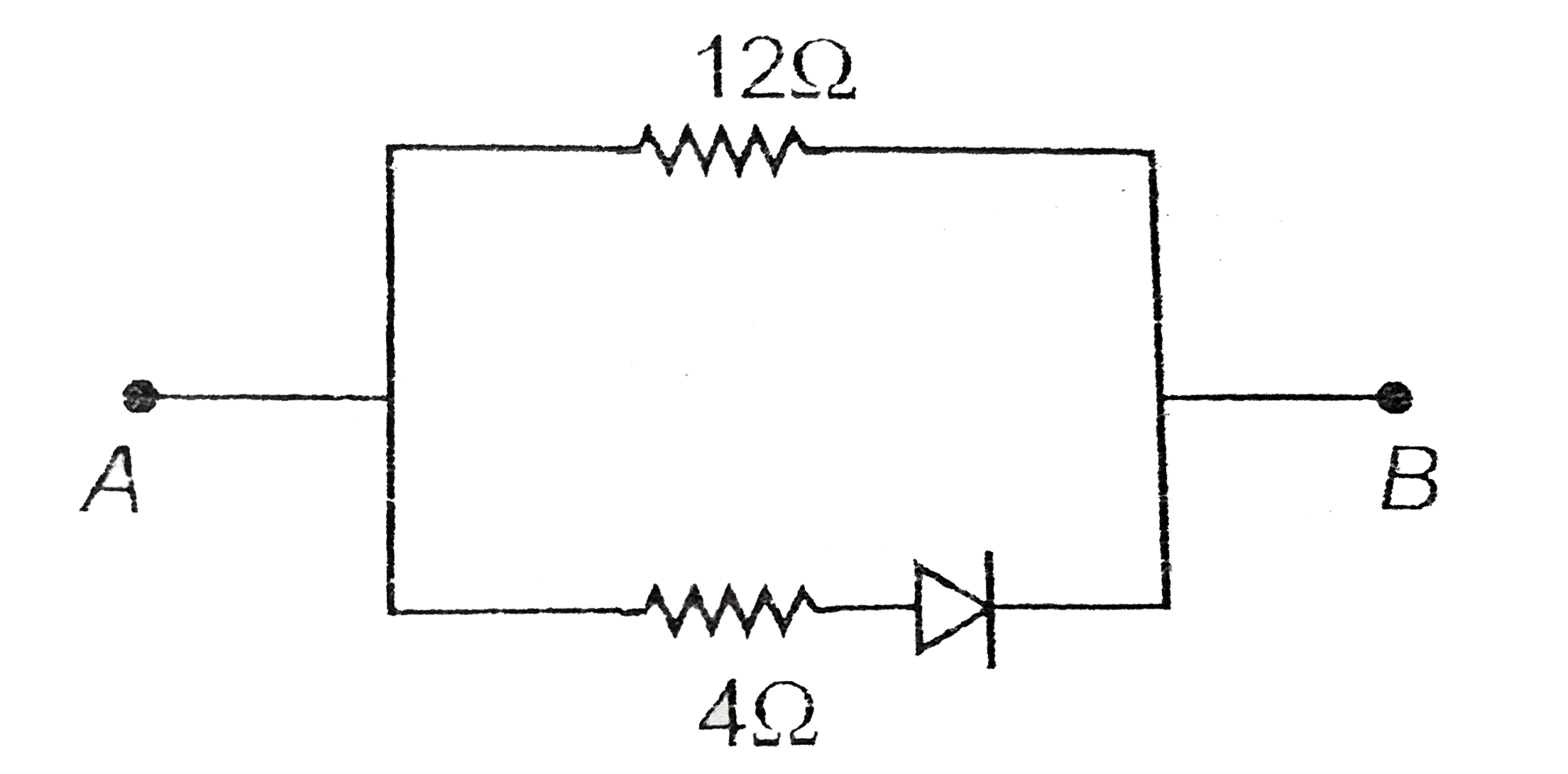
View SolutionFind the equivalent resistance of the network shown in the figure between the points A and B if
(i) VA>VB (ii) VA<VB
View SolutionGraphical soluton of a two body head on collision
A block A of mass m moving with a uniform velocity v0 strikes another identical block B kept at rest on a horizontal smooth surface as shown in the figure (i). We can conserve linear momentum.
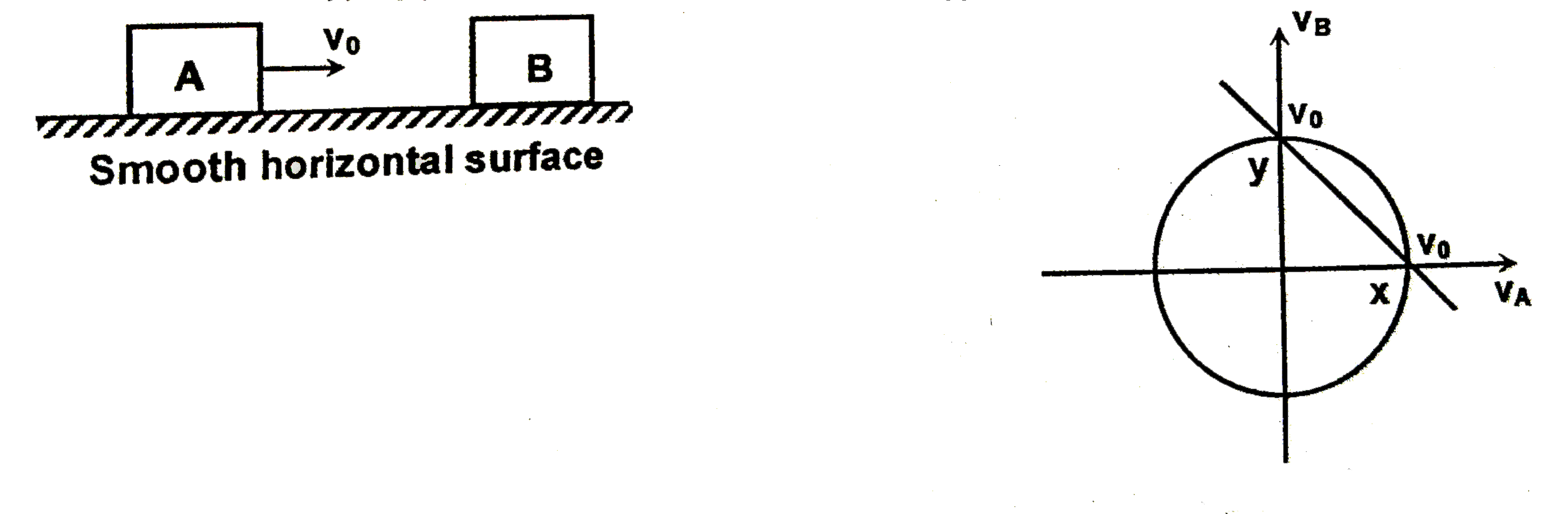
So mv0=mvAmvB (vA and vB are the velocities of the blocks after collision)
∴v0=vA+vB.........(i)
If the collision is perfectly elastic
12mv20=12mv2A+12mv2B
⇒v20=v2A+v2B......(ii)
Both the above equation (i) and (ii) are plotted on vA−vB plane as shown in figure (ii). This plot can be used to find the unknowns vA and vB.
For example the solution of the situation in figure (i) is vA=0,vB=v0 (point y in the plot)
Because vA=v0,vB=0 (point x in the plot) is not physically possible.
If the collision is perfectly inelastic, then the vA−vB plot is
View Solution