A helicopter takes off along the vertical with an acceleration a=3m/s2 and zero initial velocity. In a certain time the pilot switches off the engine. At the point of take off, the sound dies away in a time t2=30sec. Determine the velocity of the helicopter at the moment when its engine is switched off assuming that velocity of sound is 320 m/s.
The correct Answer is:80
To solve the problem, we need to determine the velocity of the helicopter at the moment when its engine is switched off. The helicopter takes off with an acceleration of a=3m/s2 and has an initial velocity of u=0.
Step 1: Determine the altitude h of the helicopter when the engine is switched off.
Using the equation of motion:
h=ut1+12at21
Since u=0, the equation simplifies to:
h=12at21
Substituting a=3m/s2:
h=12⋅3⋅t21=32t21
Step 2: Relate the time taken for sound to travel back to the ground.
The time taken for the sound to reach the ground after the engine is switched off is given as t2=30s. The sound travels at a speed of c=320m/s. The time taken for sound to travel distance h is given by:
t2=hc
Substituting the expression for h:
30=32t21320
Rearranging gives:
30⋅320=32t21
9600=32t21
Multiplying both sides by 23:
t21=9600⋅23=6400
Taking the square root:
t1=√6400=80s
Step 3: Calculate the velocity v of the helicopter when the engine is switched off.
The velocity of the helicopter at the moment the engine is switched off can be calculated using:
v=u+at1
Since u=0:
v=at1=3⋅80=240m/s
Step 4: Verify the calculations.
To ensure that the calculations are correct, we can check the values:
- The altitude h when the engine is switched off:
h=32t21=32⋅6400=9600m
- The time for sound to travel this distance:
t2=hc=9600320=30s
This confirms that our calculations are consistent.
Final Answer:
The velocity of the helicopter at the moment when its engine is switched off is:
240m/s
h=ut1+12at21
Since u=0, the equation simplifies to:
h=12at21
Substituting a=3m/s2:
h=12⋅3⋅t21=32t21
t2=hc
Substituting the expression for h:
30=32t21320
Rearranging gives:
30⋅320=32t21
9600=32t21
Multiplying both sides by 23:
t21=9600⋅23=6400
Taking the square root:
t1=√6400=80s
v=u+at1
Since u=0:
v=at1=3⋅80=240m/s
- The altitude h when the engine is switched off:
h=32t21=32⋅6400=9600m
- The time for sound to travel this distance:
t2=hc=9600320=30s
This confirms that our calculations are consistent.
The velocity of the helicopter at the moment when its engine is switched off is:
240m/s
Similar Questions
If acceleration a(t)=3t2 and initial velocity u=0 m/s , then the velocity of the particle after time t=4 s
View SolutionThe velocity of a projectile at the initial point A is (2ˆi+3ˆj)m/s. Its velocity (in m/s) at point B is

View SolutionThe acceleration of paticle varies with time as :
a(t)=3t2+4
If the initial velocity of particle is 2m/s, find the velocity of particle at t=3sec.
View SolutionFind the horizontal velocity of the particle when it reach the point Q. Assume the block to be frictionless. Take g=9.8m/s2.
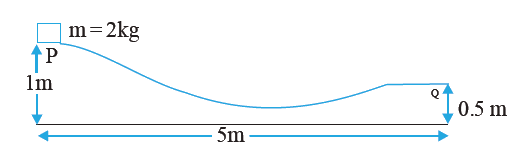
View SolutionA rocket is fired upward from the earth's surface such that it creates an acceleration of 19.6 m/sec . If after 5 sec its engine is switched off, the maximum height of the rocket from earth's surface would be
View SolutionA particle moves along the x-direction with constant acceleration. The displacement, measured from a convenient position, is 2 m at time t=0 and is zero when t=10s. If the velocity of the particle is momentary zero when t=6s, determine the acceleration a and the velocity v when t=10s.
View SolutionA siren emitting sound of frequency 800Hz is going away from a static listener with a speed of 30 m/s. Frequency of the sound to be heard by the listener is ( Take velocity of sound as 300 m/s )
View SolutionAt certain of time velocities of 1 and 2 both are 1m/s upwards. Find the velocity of 3 at that moment

View SolutionAt a certain time velocities of 1 and 2 both are 1m/s upwards. Find the velocity of 3 at that moment

View SolutionAt a certain time velocities of 1 and 2 both are 1m/s upwards. Find the velocity of 3 at that moment

View Solution
