For the reaction,
A+B→P,−d[A]dt=−d[B]dt=k[A][B]andRt=1[A0]−[B]0ln.[A][B]0[B][A]0 when [A]0≠[B]0
If [A]0=[B]0 then the integrated rate law will be
kt=ln.[A][B]
1[B]=1[A]0+kt
1[A]=1[A]0+kt
1[A]=1[A]0+ktor1[B]=1[B]0+kt
The correct Answer is:D
To solve the problem, we need to derive the integrated rate law for the reaction when the initial concentrations of A and B are equal, i.e., (A0)=(B0).
1. Understanding the Reaction:
The reaction given is:
A+B→P
The rate of the reaction is given by:
−d(A)dt=−d(B)dt=k(A)(B)
This indicates that the reaction is second-order, as it depends on the concentrations of both A and B.
2. Setting Up the Integrated Rate Law:
Since (A0)=(B0), we can denote both initial concentrations as C0:
(A0)=(B0)=C0
Thus, we can express the rate law as:
−d(A)dt=k(A)(B)=k(A)2
3. Rearranging the Rate Equation:
Rearranging the equation gives:
−d(A)(A)2=kdt
4. Integrating:
We will integrate both sides. The left side will be integrated from (A0) to (A) and the right side from 0 to t:
∫(A)(A0)−d(A)(A)2=∫t0kdt
The left side integrates to:
(1(A))(A)(A0)=1(A)−1(A0)
The right side integrates to:
kt
5. Combining the Results:
Combining the results from the integration gives:
1(A)−1(A0)=kt
Rearranging this, we have:
1(A)=1(A0)+kt
6. Substituting Back for B:
Since (A0)=(B0), we can also express this in terms of B:
1(B)=1(B0)+kt
Final Result:
Thus, the integrated rate law when (A0)=(B0) is:
1(A)=1(A0)+ktand1(B)=1(B0)+kt
The reaction given is:
A+B→P
The rate of the reaction is given by:
−d(A)dt=−d(B)dt=k(A)(B)
This indicates that the reaction is second-order, as it depends on the concentrations of both A and B.
Since (A0)=(B0), we can denote both initial concentrations as C0:
(A0)=(B0)=C0
Thus, we can express the rate law as:
−d(A)dt=k(A)(B)=k(A)2
Rearranging the equation gives:
−d(A)(A)2=kdt
We will integrate both sides. The left side will be integrated from (A0) to (A) and the right side from 0 to t:
∫(A)(A0)−d(A)(A)2=∫t0kdt
The left side integrates to:
(1(A))(A)(A0)=1(A)−1(A0)
The right side integrates to:
kt
Combining the results from the integration gives:
1(A)−1(A0)=kt
Rearranging this, we have:
1(A)=1(A0)+kt
Since (A0)=(B0), we can also express this in terms of B:
1(B)=1(B0)+kt
Thus, the integrated rate law when (A0)=(B0) is:
1(A)=1(A0)+ktand1(B)=1(B0)+kt
Similar Questions
Mechanism of the reaction is:
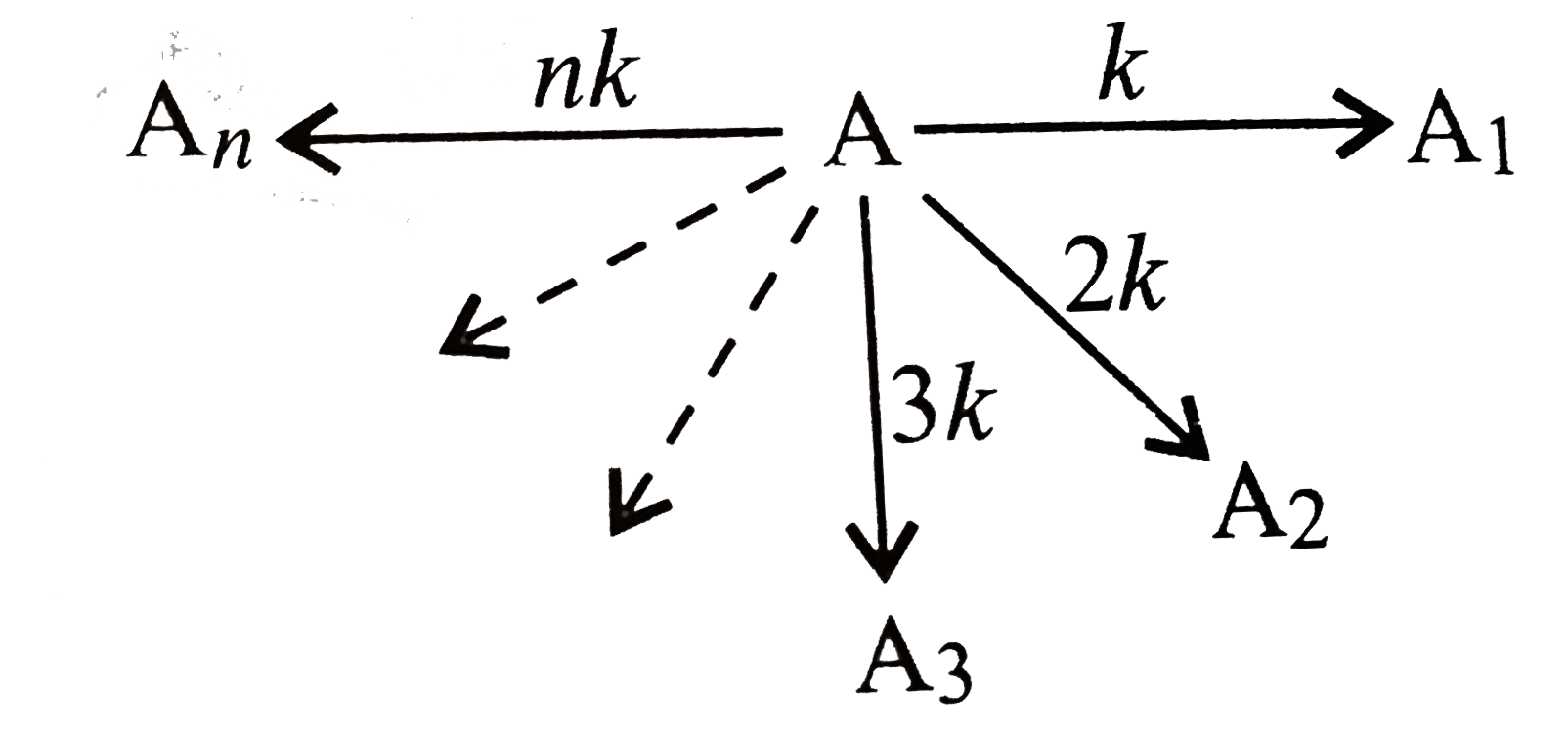
What is (a) −d[A]dt, (b) d[A1]dt
View SolutionFor the reaction in equilibrium A↔B
[B][A]=4.0×108 −d[A]dt=2.3×106S−1[A] −ddt[B]=K[B] Thus, K is
View SolutionFor the reaction: aA+bB→cC+dD
Rate =dxdt=−1ad[A]dt=−1bd[B]dt=1cd[C]dt=1dd[D]dt
In the following reaction,
xA→yB
log.[−d[A]dt]=log.[d[B]dt]+0.3
where negative isgn indicates rate of disappearance of the reactant. Thus, x:y is:
View SolutionIn the following reaction, xA→yB
log10[−d[A]dt]=log10[d([B])dt]+0.3010 ‘A’ and ‘B’ respectively can be:
View Solutiondxdt=K[A]0.5[B]0.5[C]0.5 . What will be the order of the reaction ?
View SolutionFor the reaction : aA→bB, it is given that
log[−dAdt]=log[dBdt]+0.6020. What is a:b is ?
View SolutionThe rate of the reaction A+B+C→ Product is given by: rate =−d[A]dt=k[A]1/2[B]1/4[C]0 The order of reaction is:
View SolutionFor a hypothetical reaction: A+B→ Products, the rate law is r=k[A][B]0. The order of reaction is
View SolutionIn the reaction , A+2B→6C+2D, if the initial rate −d[A]dt at t= 0 is 2.6×10−2Msec−1, what will be the value of −d[B]dt at t=0?
View SolutionSolve: xa−a+bx=b(a−b)ax, when x≠0anda≠0.
View Solution
