For the reaction in equilibrium
Thus, K is
The correct Answer is:B
To solve the problem, we need to find the equilibrium constant K for the reaction A⇌B. We are given the following information:
1. The equilibrium expression (B)(A)=4.0×108
2. The rate of change of concentration of A: −d(A)dt=2.3×106s−1
3. The rate of change of concentration of B: −d(B)dt=K(B)
Step 1: Write the equilibrium expression for the reaction.
The equilibrium constant K for the reaction A⇌B is given by:
K=(B)(A)
From the problem, we know that:
(B)(A)=4.0×108
Step 2: Relate the rates of change of concentrations.
At equilibrium, the rate of formation of B is equal to the rate of consumption of A:
−d(A)dt=d(B)dt
We can express this as:
−d(A)dt=K(B)
Step 3: Substitute the known values into the equation.
We know:
−d(A)dt=2.3×106s−1
Substituting this into the equation gives:
2.3×106=K(B)
Step 4: Express (B) in terms of (A) using the equilibrium expression.
From the equilibrium expression, we can express (B) as:
(B)=4.0×108(A)
Step 5: Substitute (B) back into the rate equation.
Now substituting (B) into the rate equation:
2.3×106=K(4.0×108(A))
Step 6: Solve for K.
Rearranging gives:
K=2.3×1064.0×108(A)
Step 7: Since we need K in terms of the equilibrium ratio, we can simplify further.
We can simplify this to:
K=4.0×1082.3×106
Step 8: Calculate K.
Calculating gives:
K≈5.8×10−3s−1
Final Answer:
Thus, the value of K is:
K≈5.8×10−3s−1
2. The rate of change of concentration of A: −d(A)dt=2.3×106s−1
3. The rate of change of concentration of B: −d(B)dt=K(B)
K=(B)(A)
From the problem, we know that:
(B)(A)=4.0×108
−d(A)dt=d(B)dt
We can express this as:
−d(A)dt=K(B)
−d(A)dt=2.3×106s−1
Substituting this into the equation gives:
2.3×106=K(B)
(B)=4.0×108(A)
2.3×106=K(4.0×108(A))
K=2.3×1064.0×108(A)
K=4.0×1082.3×106
K≈5.8×10−3s−1
Thus, the value of K is:
K≈5.8×10−3s−1
Similar Questions
A+2B→C+D. If −d[A]dt=5×10−4 mol L−1s−1, then −d[B]dt is :
View SolutionThe rate of disappearance of A at two temperature is given by A⇔B
i. −d[A]dt=2×10−2[A]−4×10−3[B] at 300K
ii. −d[A]dt=4×10−2[A]−16×10−4[B] at 400K
From the given values of heat of reaction
View SolutionFor the reaction B+2D→3T,−d[B]dt=k[B][D]2. The expression for −d[D]dt will be
View SolutionFor a reversible reaction
A+B⇔C
(dxdt)=2.0×103Lmol−1s−1[A][B]−1.0×102s−1[C] where x is the amount of 'A' dissociated. The value of equilibrium constant (Keq) is
View SolutionFor the reaction: aA+bB→cC+dD
Rate =dxdt=−1ad[A]dt=−1bd[B]dt=1cd[C]dt=1dd[D]dt
The rate of formation of SO3 in the following reaction 2SO2+O2→2SO3 is 100g−1min. Hence the rate of disappearance of O2 is
View SolutionIt is given that 0.001mol each of Cd2+ and Fe2+ ions are contained in 1.0L of 0.02MHC1 solution. This solutions is now saturated with H2S gas at 25∘C.
a. Determine whether or not each of these ions will be precipitated as sulphide?
b. How much Cd2+ ions remains in the solution at equilibrium?
K1(H2S)=1.0×10−7,K2(H2S)=1.0×10−14: ltbRgt Ksp(CdS)=8×10−27:Ksp(FeS)=3.7×10−19.
View SolutionIn the reaction , A+2B→6C+2D, if the initial rate −d[A]dt at t= 0 is 2.6×10−2Msec−1, what will be the value of −d[B]dt at t=0?
View SolutionFor the reaction: aA+bB→cC+dD
Rate =dxdt=−1ad[A]dt=−1bd[B]dt=1cd[C]dt=1dd[D]dt
A reaction follows the given concentration-time graph. The rate for this reaction at 20s will be
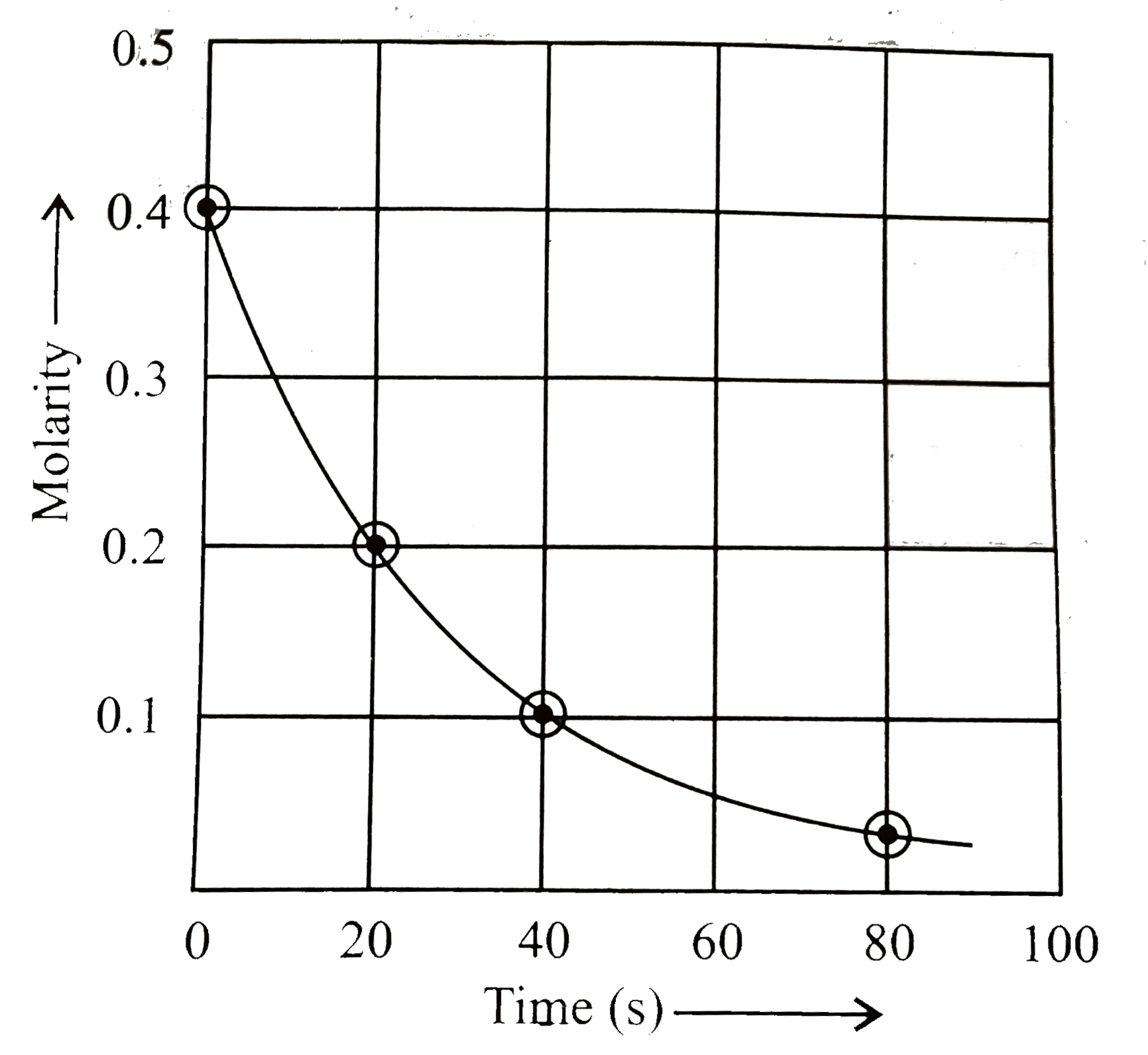
View SolutionFor the reaction: aA+bB→cC+dD
Rate =dxdt=−1ad[A]dt=−1bd[B]dt=1cd[C]dt=1dd[D]dt
In the following reaction,
xA→yB
log.[−d[A]dt]=log.[d[B]dt]+0.3
where negative isgn indicates rate of disappearance of the reactant. Thus, x:y is:
View SolutionMechanism of the reaction is:
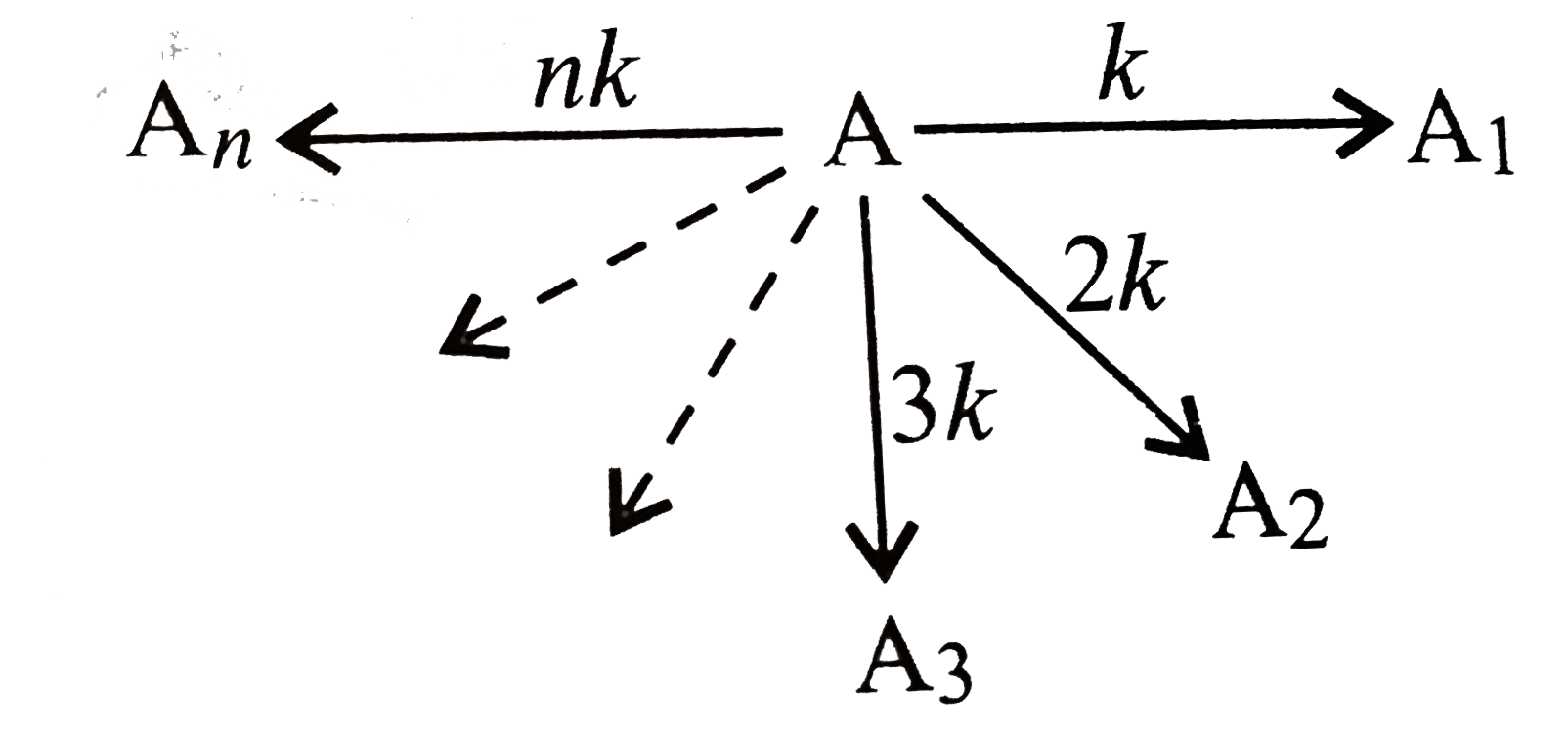
What is (a) −d[A]dt, (b) d[A1]dt
View Solution
