A40μF capacitor in a defibrillator is charged to 3000V. The energy stored in the capacitor is sent through the patient during a pulse of duration 2ms. The power delivered to the patient is
45 kW
90 kW
180 kW
360 kW
The correct Answer is:B
To solve the problem, we need to find the power delivered to a patient by a defibrillator, which involves a capacitor. Here's a step-by-step solution:
Step 1: Calculate the Energy Stored in the Capacitor
The energy (E) stored in a capacitor can be calculated using the formula:
E=12CV2
where:
- C is the capacitance in farads,
- V is the voltage in volts.
Given:
- C=40μF=40×10−6F
- V=3000V
Substituting the values into the formula:
E=12×(40×10−6)×(3000)2
Calculating (3000)2:
(3000)2=9000000
Now substituting back:
E=12×(40×10−6)×9000000
E=20×10−6×9000000
E=180J
Step 2: Calculate the Power Delivered to the Patient
Power (P) is defined as the energy delivered per unit time:
P=Et
where:
- E is the energy in joules,
- t is the time in seconds.
Given:
- t=2ms=2×10−3s
Substituting the values:
P=180J2×10−3s
P=1800.002
P=90000W
P=90kW
Final Answer
The power delivered to the patient is:
Power=90kW
The energy (E) stored in a capacitor can be calculated using the formula:
E=12CV2
where:
- C is the capacitance in farads,
- V is the voltage in volts.
- C=40μF=40×10−6F
- V=3000V
E=12×(40×10−6)×(3000)2
(3000)2=9000000
E=12×(40×10−6)×9000000
E=20×10−6×9000000
E=180J
Power (P) is defined as the energy delivered per unit time:
P=Et
where:
- E is the energy in joules,
- t is the time in seconds.
- t=2ms=2×10−3s
P=180J2×10−3s
P=1800.002
P=90000W
P=90kW
The power delivered to the patient is:
Power=90kW
Similar Questions
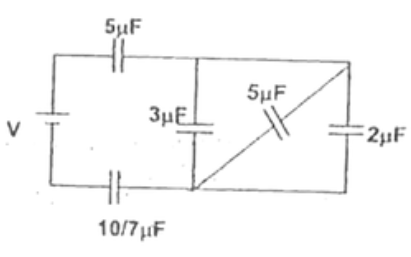
If potential difference across 3μF is 4V, then total energy stored in all capacitors is
View SolutionA capacitor is connected across an inductor. At time t = 0 charge on the capacitor is equal to 1√2qmax, where qmax is the maximum charge on the capacitor. The time t, at which the energy stored in the capacitor is equal to the energy stored in the inductor is (The inductance of the inductor is L and capacitance of the capacitor is C. Resistance of the circuit is zero)
View Solution
Knowledge Check
A capacitor of capacitance 700 pF is charged by 100 V battery. The electrostatic energy stored by the capacitor is
A2.5×10−8JB3.5×10−6JC2.5×10−4JD3.5×10−4JEnergies stored in capacitor and dissipated during charging a capacitor bear a ratio
A1:1B1:2C2:1D1:3
A 8uF capacitor C1 is charged to V0=120V. The charging battery is then removed and the capacitor is connected in parallel to an uncharged +4μF capacitor C2.
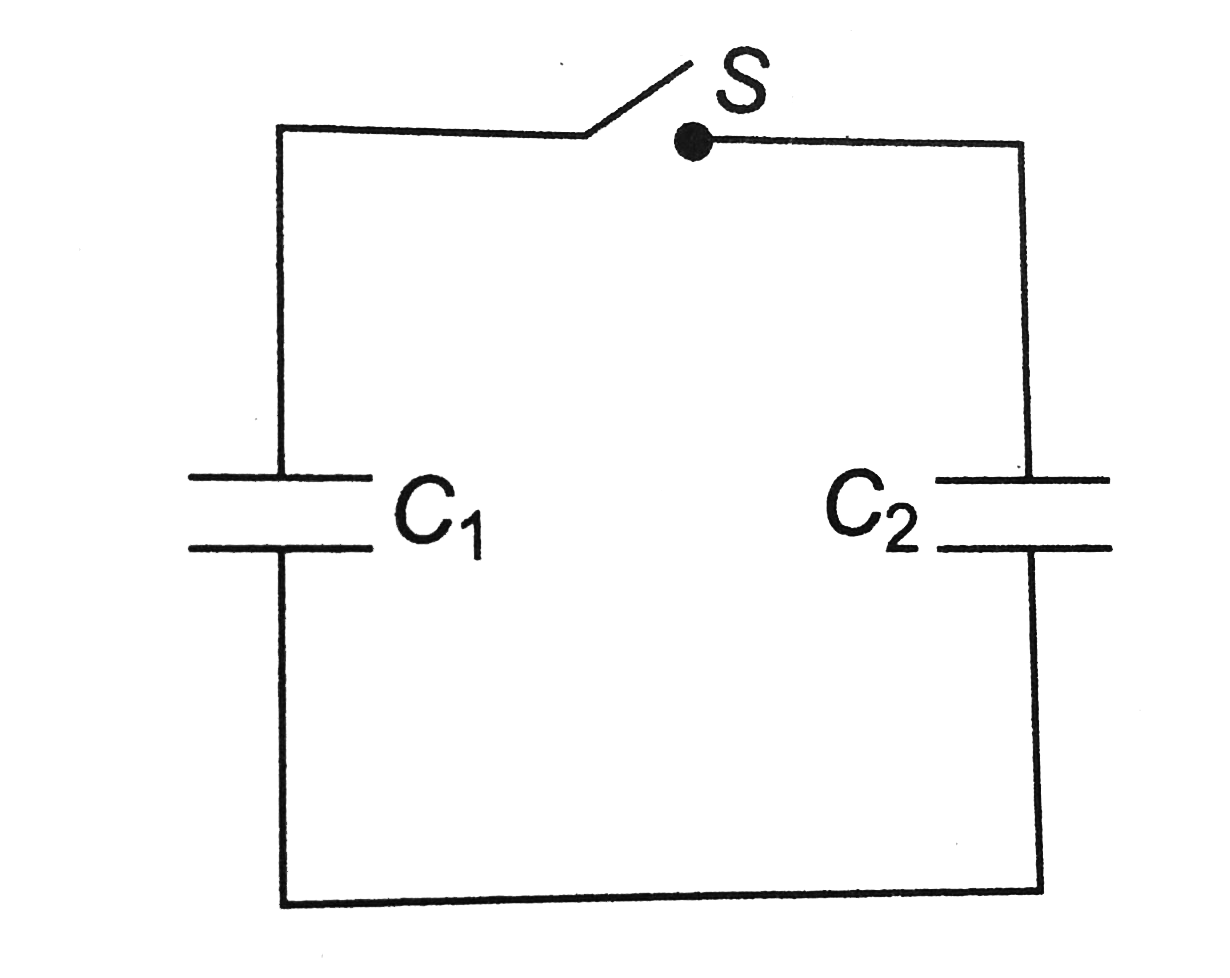
(a) what is the potential difference V across the combination?
(b) what is the stored energy before and after the switch S is closed?
View SolutionFind the energy stored in a capacitor of capacitance 100μF when it is charged to a potential difference of 20 V.
View SolutionA capacitor of capacitor 5.00μF is charged to24.0V and another capacitor of capacitance 6.0μF is charged to 12.0V (a) Find the energy stored in each capacitor .(b)The positive plates of the first capacitor is now connected to the negative plate of the second and vice versa . Find the new charges on the capacitors .(c)Find the loss of electrostatic energy during the process .(d)Where does this energy go?
View SolutionA capacitor of capacity C hasd charge Q and stored energy is W. if the charge is increased to 2Q, then the stored energy will be
View SolutionThree capacitors having capacitances of 8.4μF,8.4μF and 4.2μF are connected in series across a 36 potential difference.
(a) What is the charge on 4.2μF capacitor?
(b) What is the total energy stored in all three capacitors?
(c) The capacitors are disconnected from the potential difference without allowing them to discharge. They are then reconnected in parallel with each other, with the positively charged plates connected together. What is the voltage across each capacitor in the parallel combination?
(d) What is the total energy now stored in the capacitors?
View SolutionA parallel plate capacitor of capacity C0 is charged to a potential V0,E1 is the energy stored in the capacitor when the battery is disconnected and the plate separation is doubled, and E2 is the energy stored in the capacitor when the charging battery is kept connected and the separation between the capacitor plates is dounled. find the ratio E1/E2.
View Solution
