A capacitor of capacity C hasd charge Q and stored energy is W. if the charge is increased to 2Q, then the stored energy will be
2W
W/2
4W
W/4
The correct Answer is:C
To solve the problem, we need to determine how the stored energy in a capacitor changes when the charge is increased from Q to 2Q.
1. Understand the formula for stored energy in a capacitor:
The energy W stored in a capacitor can be expressed using the formula:
W=12Q2C
where Q is the charge and C is the capacitance.
2. Substitute the initial charge:
For the initial condition where the charge is Q, the stored energy is:
W=12Q2C
3. Increase the charge to 2Q:
Now, if the charge is increased to 2Q, we need to calculate the new stored energy W′:
W′=12(2Q)2C
4. Calculate (2Q)2:
Simplifying (2Q)2:
(2Q)2=4Q2
Therefore, we can rewrite the expression for W′:
W′=124Q2C
5. Factor out the original energy:
We can factor out the original energy W from this expression:
W′=4(12Q2C)=4W
6. Conclusion:
Thus, when the charge is increased to 2Q, the stored energy becomes:
W′=4W
Final Answer:
The stored energy will be 4W.
---
The energy W stored in a capacitor can be expressed using the formula:
W=12Q2C
where Q is the charge and C is the capacitance.
For the initial condition where the charge is Q, the stored energy is:
W=12Q2C
Now, if the charge is increased to 2Q, we need to calculate the new stored energy W′:
W′=12(2Q)2C
Simplifying (2Q)2:
(2Q)2=4Q2
Therefore, we can rewrite the expression for W′:
W′=124Q2C
We can factor out the original energy W from this expression:
W′=4(12Q2C)=4W
Thus, when the charge is increased to 2Q, the stored energy becomes:
W′=4W
The stored energy will be 4W.
Topper's Solved these Questions
- ELECTROSTATIC POTENTIAL AND CAPACITORSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - (B) Chapter exercises
17 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITORSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - (C) Chapter exercises
50 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITORSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - Check point 2.5
20 Videos
- ELECTROMAGNETIC WAVESBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Sec C
22 Videos
- ELECTROSTATICSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Medical entrances gallery
37 Videos
Similar Questions
A capacitor of capacitance 15μF has a charge 30μC and stored energy is W. If charge increased to 60μC the energy stored will be.
View SolutionA parallel plate capacitor of capacity C0 is charged to a potential V0,E1 is the energy stored in the capacitor when the battery is disconnected and the plate separation is doubled, and E2 is the energy stored in the capacitor when the charging battery is kept connected and the separation between the capacitor plates is dounled. find the ratio E1/E2.
View Solution
Knowledge Check
A capacitor of capacitance 700 pF is charged by 100 V battery. The electrostatic energy stored by the capacitor is
A2.5×10−8JB3.5×10−6JC2.5×10−4JD3.5×10−4J
A capacitor is charge until it stores an energy of 1J. A second uncharged capacitor is connected to it, so that charge districutes equally. The final energy stored in the second capacitor is
View SolutionA parallel plate capacitor of capacitane C is charged to a potential V. It is then connected to another uncharged capacitor with the same capacitance. Find out the ratio of the energy stored in the combined system to that stored initially in the single capacitor.
View SolutionA cylindrical capacitor has charge Q and length L. If both the charge and length of the capacitor are doubled by keeping other parameters fixed, the energy stored in the capacitor
View SolutionFind the charged stored in all the capacitors
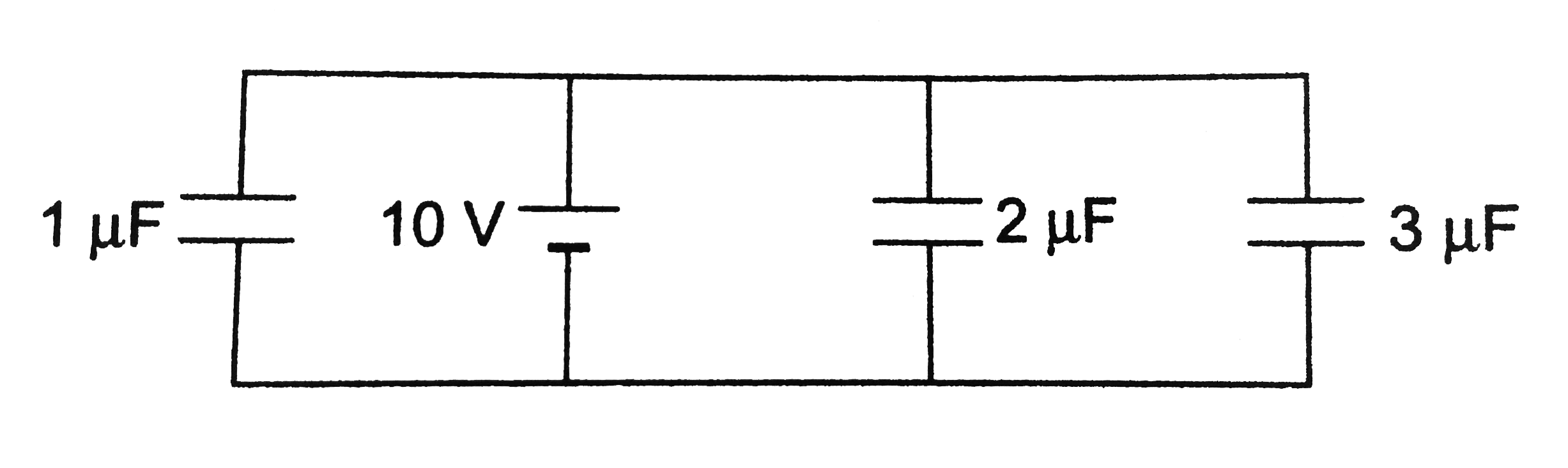
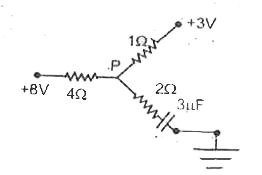
View SolutionThe energy stored in the capacitor in the steady state is
View SolutionA capacitor of 2μF is charged as shown in the figure. When the switch S is turned to position 2, the percentage of its stored energy dissipated is

View SolutionA capacitor is connected across an inductor. At time t = 0 charge on the capacitor is equal to 1√2qmax, where qmax is the maximum charge on the capacitor. The time t, at which the energy stored in the capacitor is equal to the energy stored in the inductor is (The inductance of the inductor is L and capacitance of the capacitor is C. Resistance of the circuit is zero)
View Solution
